Модель дпт

Модель двигателя постоянного тока так же, как и генератора, включает в себя две модели: модель якорной цепи и модель цепи возбуждения. Модель цепи возбуждения ДПТ аналогична модели цепи возбуждения ГПТ. При учете насыщения магнитной системы:

,

,

где Φ_VM - поток полюса ДПТ; i_VM - ток обмотки возбуждения ДПТ; L_VM - индуктивность обмотки возбуждения ДПТ.

Если насыщение магнитной системы двигателя не учитывать, то индуктивность ДПТ будет постоянной, а поток полюса двигателя будет определяться соотношением:

,

где k_SVM - коэффициент схемы соединения обмоток полюсов ДПТ; k_SVM = 2pw_VM для последовательного соединения обмоток полюсов и k_SVM = pw_VM/2 для параллельно-последовательного соединения; w_VM - число витков обмотки полюса генератора.

Ток обмотки возбуждения ДПТ определяется по выражению:

,

где p = d/dt - оператор дифференцирования; R_VM - активное сопротивление обмотки возбуждения (зависит от схемы включения обмоток полюсов); T_VM = L_VM/R_VM.

Модель якоря ДПТ можно получить из схемы замещения якорной цепи (рис. 14):

,

где u_AM - напряжение, подводимое к якорю ДПТ; R_AM = RM_дп+RM_ко+RM_а - полное активное сопротивление якорной цепи ДПТ; L_AM = LM_дп+LM_ко+LM_а - полная индуктивность якорной цепи ДПТ; e_АМ = k_МΦ_VMω_M - ЭДС якоря ДПТ; k_M = pN/2πa - конструктивный коэффициент ДПТ; ω_M - частота вращения якоря ДПТ в рад/с.

Рис. 14. Принципиальная электрическая схема и схемы замещения ДПТ

Структурная схема ДПТ показана на рис. 15. Под действием подводимого к двигателю напряжения, начинает протекать электрический ток в обмотке якоря. Ток якоря, взаимодействуя с магнитным потоком обмотки возбуждения, создает электромагнитный момент, способствующий вращению якоря ДПТ. При вращении якоря ДПТ под действием магнитного потока возбуждения образуется ЭДС вращения в обмотке якоря. ЭДС с ростом частоты вращения якоря приводит к уменьшению тока якоря, а, следовательно, и электромагнитного момента ДПТ до тех пор, пока не установится равновесие. Время разгона якоря ДПТ до установившейся скорости определяется суммарным приведенным моментом инерции нагрузки и самого двигателя J, а также моментом сопротивления нагрузки М_с.

Рис. 15. Структурная схема ДПТ при учете

насыщения магнитной системы

Модель мпу

Модель механического передаточного устройства электропривода (МПУ) обычно представляют в виде одномассовой или многомассовой системы. Если коэффициенты жесткости элементов МПУ малы, то пренебрежение ими дает неточность при расчетах и моделировании. В данном методическом пособии будем использовать модель МПУ с одним упругим звеном [2]:

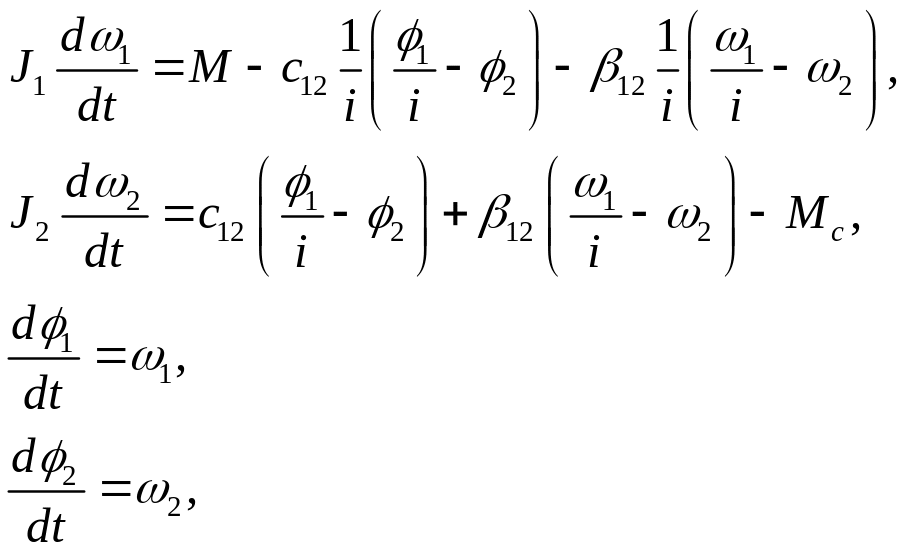
где с₁₂ - крутильная жесткость упругого звена; β₁₂ - коэффициент вязкого трения упругого звена; i = ω_2n/ω_1n - коэффициент передачи МПУ; ω_1n, ω_2n - номинальные частоты вращения входного и выходного валов МПУ; J₁ - момент инерции первой массы, приведенной к валу двигателя; J₂ - момент инерции второй массы, приведенный к выходному валу МПУ.

Упругое звено передает крутящий момент от двигателя к рабочему органу машины. Если рабочий орган совершает линейные перемещения, то для определения момента сопротивления, создаваемого рабочим органом, необходимо воспользоваться соотношением:

где F_c - усилие, создаваемое рабочим органом; R - радиус барабана или шестерни, преобразующей вращательное движение в поступательное.

Из частоты вращения выходного конца упругого звена можно вычислить линейную скорость рабочего органа:

V₂ = ω₂R.

Структурная схема МПУ представлена на рис. 16.

Рис. 16. Структурная схема МПУ с одним упругим звеном