Лабораторная работа № 1 исследование характеристик элементарных звеньев

Содержание работы

Моделирование устойчивых апериодических и колебательных звеньев с помощью персональной ЭВМ. Исследование влияния параметров звеньев на переходные процессы с использование пакета Control Toolbox системы MATLAB.

1. Теория и методические указания

Произвольную систему автоматического управления можно рассматривать как совокупность целого ряда составных частей — звеньев. Членение на звенья можно осуществлять как по функциональному признаку (измерительные, усилительно-преобразовательные звенья, приводы), так и по характеру передаточной функции САУ в разомкнутом состоянии, путем ее разложения на элементарные множители

Каждый элементарный множитель можно считать передаточной функцией некоторого передаточного звена.

Таким образом, при изучении процессов управления все многообразие САУ можно рассматривать как различные комбинации из небольшого количества стандартных элементов — элементарных звеньев.

1.Устойчивым апериодическим звеном называется звено с передаточной функцией

Свойства такого звена определяются одним параметром Т. Этот параметр называется постоянной времени и имеет размерность [сек]. По передаточной функции, которая представляет собой отношение изображения по Лапласу выходного сигнала (у) к изображению сигнала, поданного на вход звена (х), нетрудно определить дифферециальное уравнение апериодического звена:

(1)

Если входной сигнал имеет форму единичного скачка, т.е. х = 1 при

t  0 и х = 0 при t < 0 , то у = f (t) называется переходной функцией или переходным процессом (h (t)). Переходная функция устойчивого апериодического звена является решением дифференциального уравнения (1) при х = 1 и имеет вид:

(2)

График ее приведен на рис. 1. Он имеет непериодический характер, отсюда и название звена.

Как видно из формулы (2), характер переходного процесса апериодического звена полностью определяет постоянная времени. Ее величину можно определить по графику переходного процесса. При t = T получим (см. рис. 1). Если скачкообразный входной сигнал не единичный (х = с), то при t = T имеет место равенство: y = 0,632c

.

y

1

0,95y_уст

0 ,632у_уст

t

0 Т t_р 5 10

Рис. 1. График переходного процесса устойчивого апериодического звена

Хотя постоянная времени полностью определяет апериодический переходный процесс, для оценки качества процесса используется величина, характеризующая его более наглядно. Эта величина называется временем переходного процесса или временем регулирования t_р. Этот промежуток времени, по истечении которого переходный процесс практически заканчивается (h(t_р) = 0,95с). С помощью уравнения (2) нетрудно установить связь между t_р и Т.

Отсюда следует

Хотя характеристики переходного процесса апериодического звена, как и других элементарных звеньев, нетрудно определить аналитически, моделирование этих звеньев имеет большой практический интерес, т.к. является необходимым элементом моделирования систем автоматического управления.

2.Устойчивым колебательным звеном называется элементарное звено с передаточной функцией

при 0 <  < 1.

Свойства колебательного звена определяются уже двумя параметрами: Постоянной времени Т и относительным коэффициентом демпфирования .

Дифферециальное уравнение звена имеет вид

Его решение при х = 1 дает переходную функцию:

(4)

Если считать аргументом отношение , то согласно формуле (4) характер переходного процесса будет зависеть только от коэффициента . Постоянная времени изменяет лишь масштаб переходного процесса по времени.

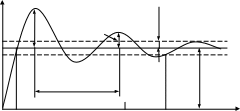
На рис. 2 приведен график переходного процесса устойчивого колебательного звена. Он имеет колебательный характер и для его оценки уже не достаточно одного времени переходного процесса.

Колебательные переходные процессы характеризуются также:

а) временем срабатывания t_c (см. рис. 2),

б) относительным перерегулированием или относительным забросом

в) показателями колебательности, которую можно оценить отношением двух смежных амплитуд или относительным изменением амплитуды (затуханием) за период .

г) временем регулирования t_р

y

A₁ A₂ 0,05у_уст

1

T_св у_уст

t

0

t_c 10 t_р

Рис. 2. График переходного процесса устойчивого колебательного звена

Из формулы (4) следует, что такие характеристики переходного процесса устойчивого колебательного звена как и оценки колебательности зависят только от одного параметра этого звена —относительного коэффициента демпфирования .