2. Неоднородности в линиях передачи. Согласование линий передачи

2.1. Описание электромагнитного процесса в линиях передачи с неоднородностями

В технике сверх- высоких частот на основе волноводов проектируются устройства различного функционального назначения: фильтры, делители мощности, ответвители и т.д. Любое устройство создается с помощью различных вида перегородок, металлических штырей, диэлектрических шайб и т.п., устанавливаемых в поперечно сечении волновода. На рис. 2.1. показаны некоторые виды металлических перегородок и штыря в прямоугольном волноводе. В электродинамике их принято называть неоднородностями. Неоднородности возникают на стыках линий передачи разных размеров поперечных сечений линий передачи.

Анализ электромагнитного процесса в линиях передачи содержащих неоднородности строится в предположении, что в них распространяется только один основной тип волны: H₁₀ в прямоугольном волноводе, H₁₁ в кругом волноводе, ТЕМ в линиях передачи. Поле основной волны в месте расположения неоднородности возбуждает поля высших типов, которые не распространяются по линии передачи, а локализуются вблизи неоднородности. Совокупное электромагнитное поле высших типов волн связано с реактивной энергией, локализующейся вблизи неоднородности. В зависимости от вида неоднородности энергия может накапливаться преимущественно в совокупном магнитном поле, либо в электрическом поле. В зависимости от этого неоднородности можно характеризовать соответствующими эквивалентными параметрами – индуктивными или емкостными. Толщина перегородок, диаметры штырей и т.д. обычно много меньше длины волны в линии передачи, поэтому в ряде случаев их можно считать бесконечно тонкими. Это в свою очередь позволяет считать, что неоднородность не занимает физического объема и, следовательно, ее индуктивную или емкостную реакцию можно соотнести с эквивалентным индуктивным или емкостным сопротивлением (проводимостью) включенным в линию передачи. Представление неоднородностей в виде эквивалентных реактивных сопротивлений неточно, потому, что всякая неоднородность поглощает электромагнитную энергию и, следовательно, имеет активную составляющую эквивалентного сопротивления, но ею можно пренебречь при упрощенном анализе.

Перейдем к описанию электромагнитного процесса в линии передачи с неоднородностью. На рис. 2.2. представлено сечение условной линии передачи в плоскости оси распространения электромагнитной волны. В сечении z=0 расположена неоднородность. Исходным условием анализа является одномодовый режим работы линии передачи. В этом случае, от генератора распространяются падающие волны напряжения и тока

, . (2.1)

Мощность падающей волны равна

,

где , - связаны через волновое сопротивление линии

.

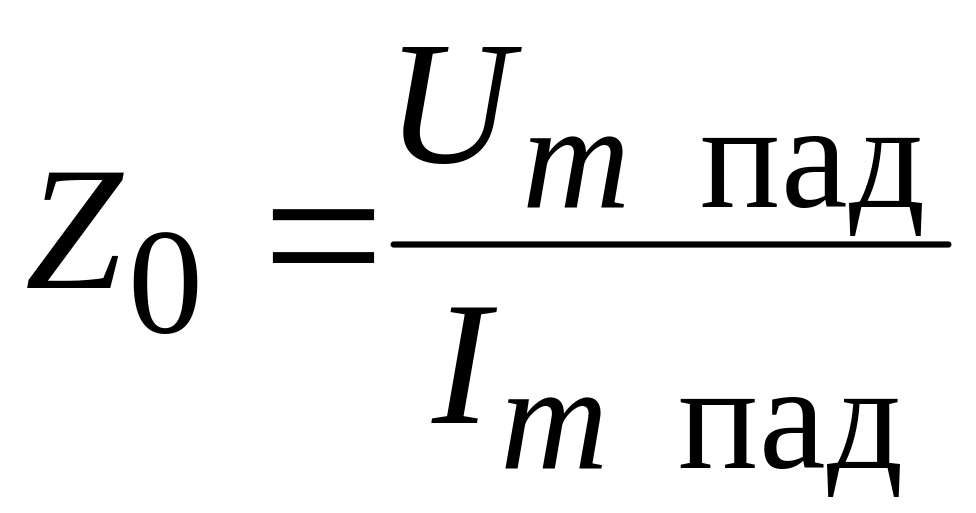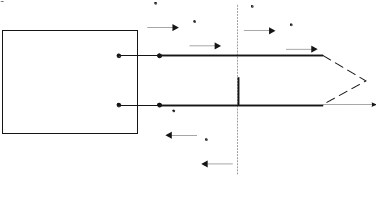
При падении волны на неоднородность возникают не только волны высших типов локализующиеся в малом объеме, но и отраженная волна основного типа, распространяющаяся в сторону генератора рис. 2.2. Отраженные волны идентичны падающим и отличаются только значениями амплитуды и фазы. Запишем отраженные волны напряжения и тока в виде

, . (2.2)

Отрицательный знак у , определен распространение волны тока в сторону отрицательного направления оси . Фазовый сдвиг в отраженной волне определяется видом неоднородности.

Свойства неоднородности удобно характеризовать коэффициентом отражения. Коэффициент отражения по напряжению в сечении неоднородности определяется как

.

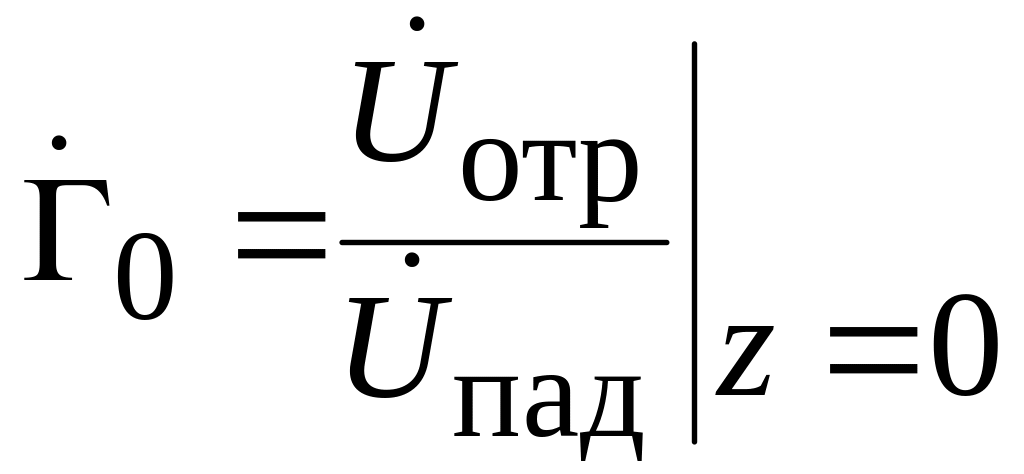Подставим сюда соотношения (2.1) и (2.2), получим

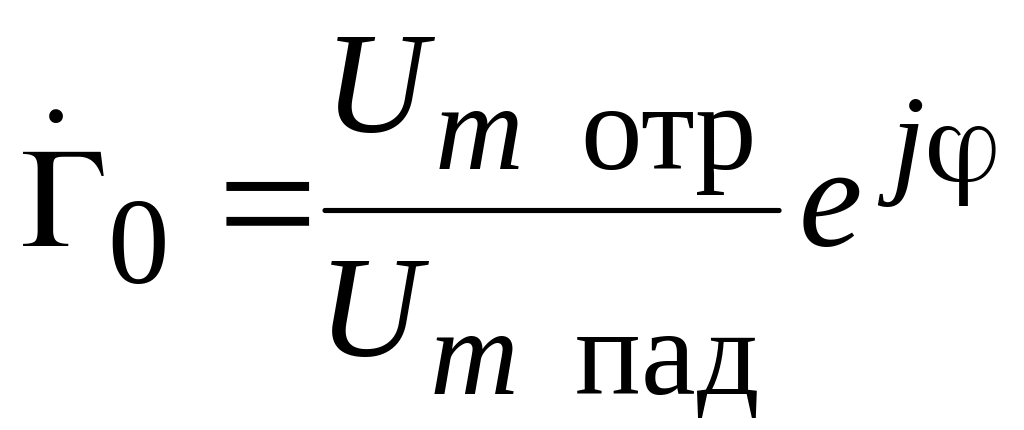. (2.3)

Коэффициент отражения в сечении неоднородности является величиной комплексной: его модуль равен отношению амплитуд напряжения отраженной и падающей волн, а фаза, равна фазе отраженной волны.

Коэффициент отражения по току определяется как

.

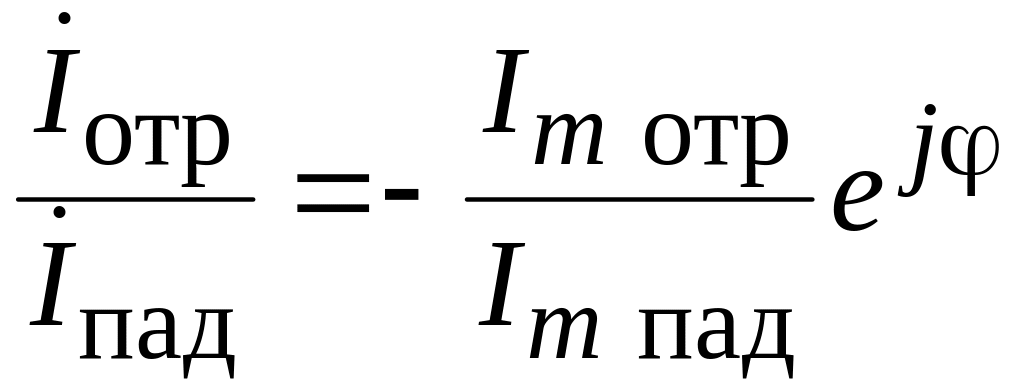Амплитуды тока в падающей и отраженной волне пропорциональны амплитудам напряжения (2.1), поэтому

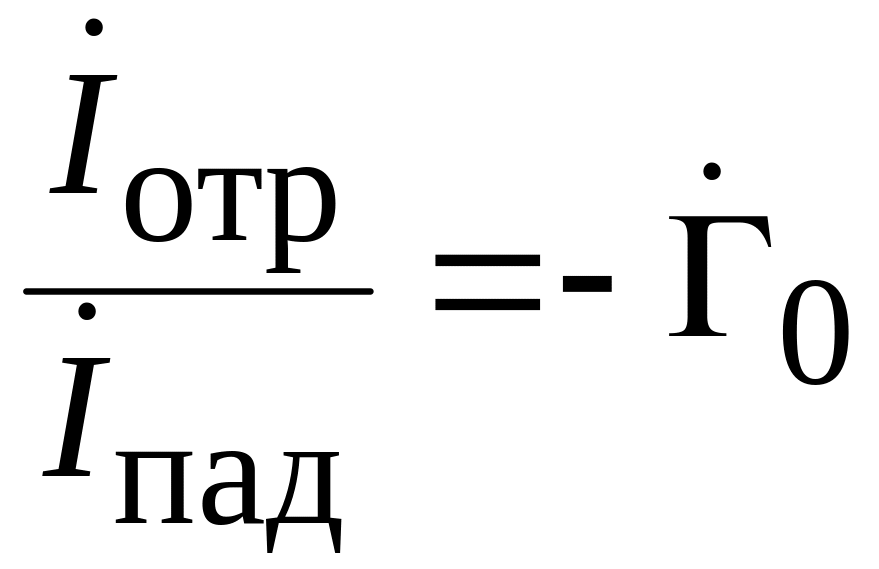. (2.4)

В пространстве между генератором и неоднородностью возникает наложение падающих и отраженных волн. В соответствии с (2.1) и (2.2), найдем их суммы

,

(2.5)

.

Используя соотношения (2.3) и (2.4) преобразуем (2.5) к виду

,

(2.6)

.

Из (2.6) следует, что в результирующих волнах амплитуды напряжения и тока изменяются в зависимости от удаления от неоднородности как

,

(2.7)

.

Такие волны называют стоячими, а величину

, (2.8)

коэффициентом отражения в плоскости z. Его модуль равен модулю , а фаза является непрерывной функцией z.

Найдем явный вид зависимости от амплитуды напряжения стоячей волны. В соответствии с (2.7) и (2.3) запишем

. (2.9)

Соотношение (2.9) можно преобразовать к виду

. (2.10)

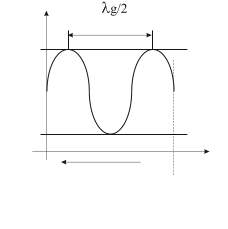Из (2.10) следует, что амплитуда стоячей волны периодически изменяется между максимальным и минимальным значениями с периодом по оси z равным половине длины волны в линии, что определяется аргументом косинуса в (2.10). На рис. 2.3, изображен график зависимости амплитуды стоячей волны от удаления от неоднородности в сторону генератора.

В инженерной практике отношение максимального значения амплитуды стоячей волны к минимальному значению называется коэффициентом стоячей волны по напряжению (КСВН)

.

Как видно КСВН изменяется в интервале в зависимости от значения .

Рассмотрим соотношения между мощностями в падающей и отраженной волне. Мощность отраженной волны равна

. (2.11)

Отрицательный знак в (2.11) определен распространением отраженной волны вдоль отрицательного направления оси . Подставим в (2.11) соотношение (2.2) получим

. (2.12)

Амплитуды отраженных и падающих волн связаны между собой модулем коэффициента отражения (2.3), (2.4). Поэтому , . Подставим эти соотношения в (2.12), найдем мощность отраженной волны

.

В соответствии с балансом мощностей найдем мощность прошедшей волны

, (2.13)

где - квадрат модуля коэффициента отражения.