1.4. Коаксиальные линии

Рис. 1.5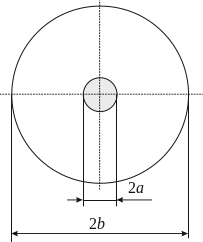

Коаксиальная линия представляет собой два соосных металлических цилиндра рис. 1.5, разделенных либо воздушным промежутком, либо диэлектриком. Этим конструкциям отвечает жесткая коаксиальная линия, либо коаксиальный кабель. В качестве диэлектрика в кабеле используются полимерные материалы с относительной диэлектрической проницаемостью . Принципиальное отличие коаксиальных линий от волноводов состоит в том, что в них основным типом волны является поперечная волна ТЕМ с f_гр=0. Очевидно, что наличие двух изолированных проводников в структуре линии, позволяет передавать постоянный ток. Верхнее значение рабочей частоты линии ограничено появлением волны ближайшего высшего типа, которой является волна Н₁₁. Ее граничная частота равна 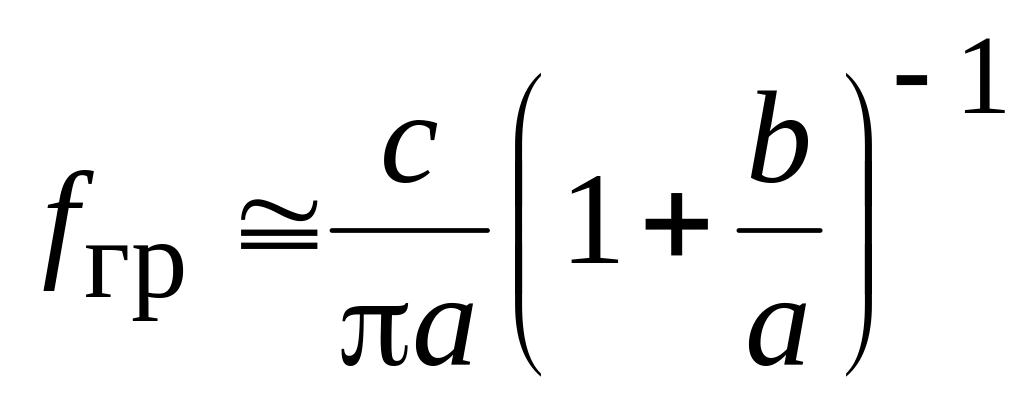, и таким образом полоса частот одномодового режима коаксиальной линии ограничена значением f_гр.

Электромагнитное поле коаксиальной линии на поперечном сечении имеет квазистатический характер. Поэтому магнитное поле коаксиальной линии идентично полю линейного постоянного тока. Обозначим - амплитуду тока в центральном проводнике коаксиальной линии и запишем магнитное поле в виде

где r – координата на поперечном сечении.

Напряженность электрического и магнитного поля в ТЕМ волне связаны между собой соотношением

,

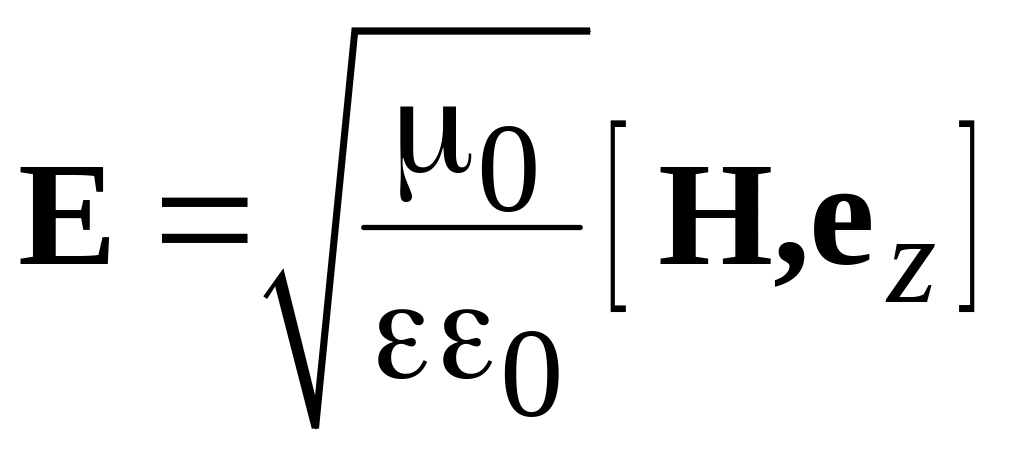откуда следует, что

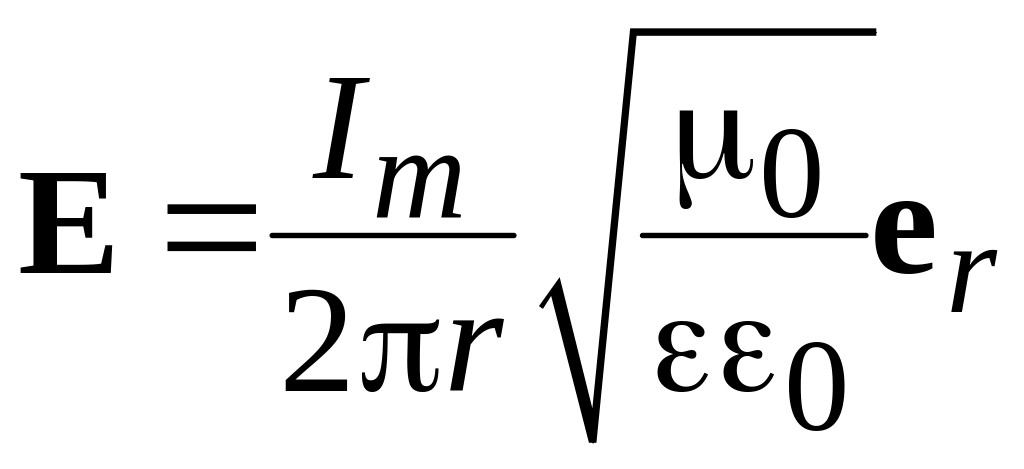. (1.12)

В силу потенциального характера поля в ТЕМ волне амплитуду напряжения между проводниками коаксиальной линии можно найти интегрированием напряженности поля (1.12) по радиусу

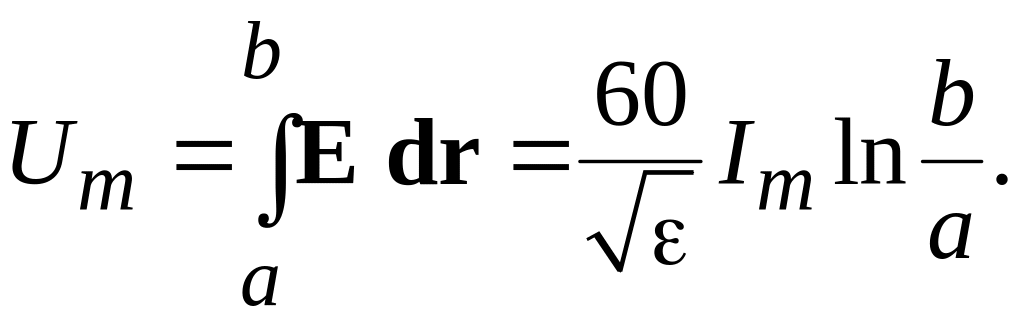(1.13)

Отношение амплитуды напряжения к амплитуде тока называется волновым сопротивлением линии

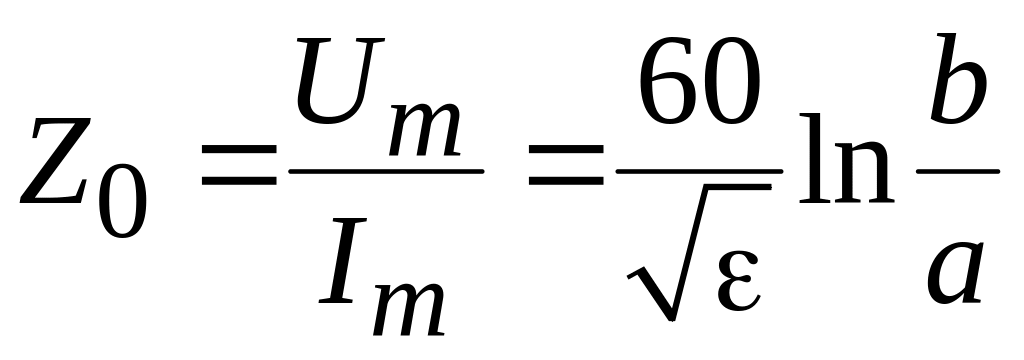. (1.14)

Для коаксиальных линий, как и волноводов, важны такие характеристики как полоса рабочих частот, максимальная передаваемая мощность и затухание.

Мощность, передаваемую по коаксиальной линии, найдем интегрированием комплексного вектора Пойнтинга по поперечному сечению

,

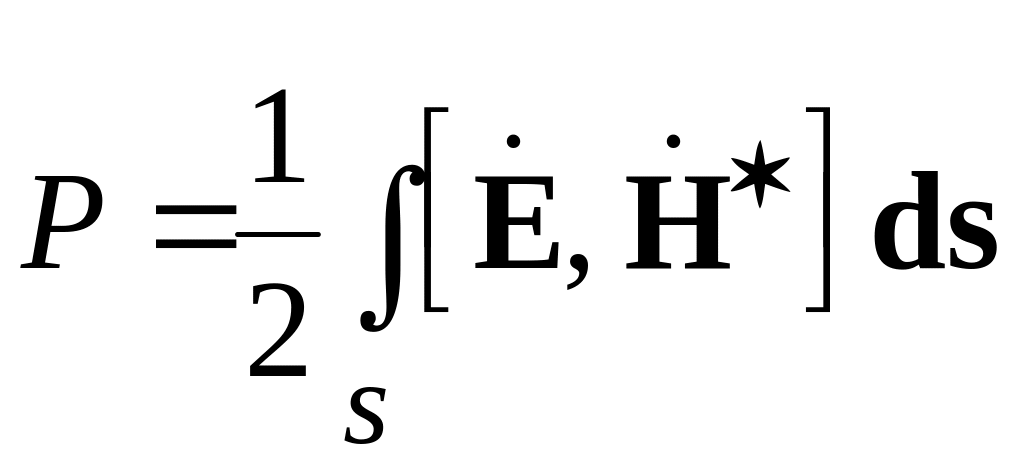где - элемент интегрирования в полярной системе координат. Подставим сюда напряженности полей, получим

.

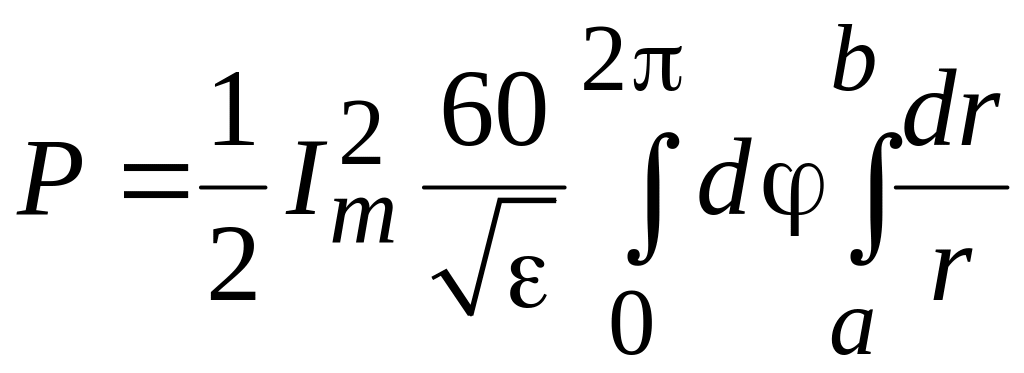Откуда следует, что

. (1.15)

На основании (1.14) и (1.15) получим

.

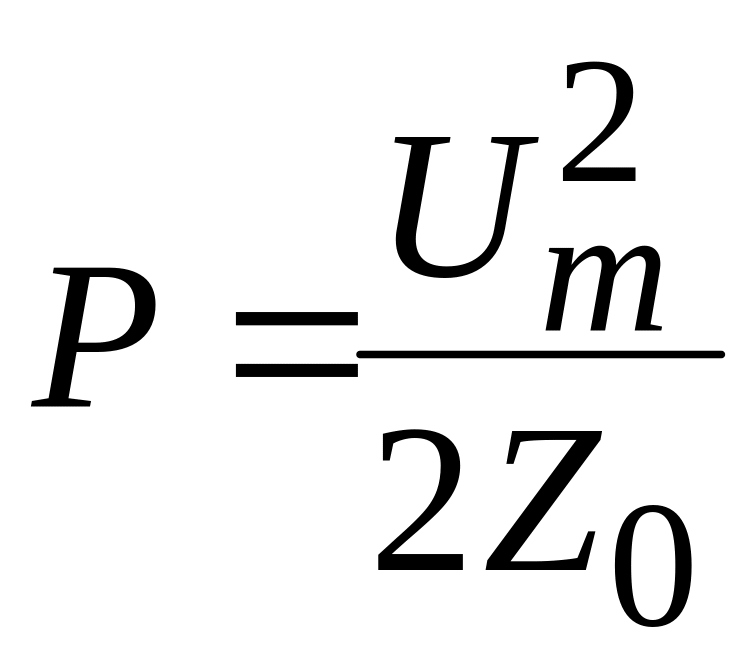Из (1.15) следует, что в соответствии с законом Джоуля-Ленца волновое сопротивление линии является нагрузкой для источника поля, подключенного к линии.

С помощью соотношение (1.13) и (1.12) можно связать значения амплитуды напряжения с напряженностью электрического поля. Из (1.12) следует, что максимальная напряженность поля возникает на поверхности внутреннего проводника, . Поэтому в соответствии с (1.15) и (1.13) найдем, максимальную мощность, передаваемую по линии

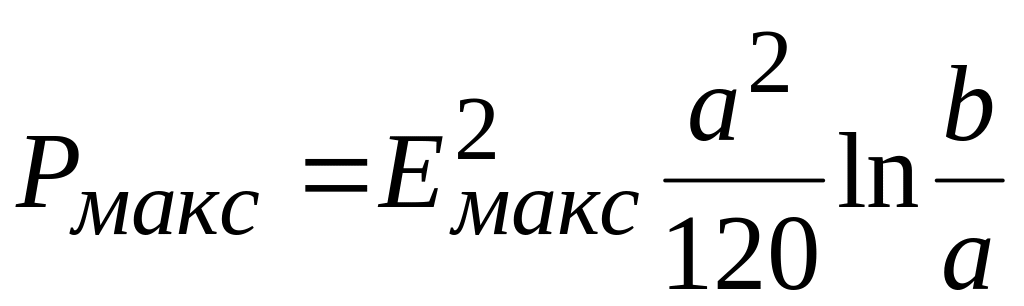. (1.16)

Из (1.16) следует, что максимальная передаваемая мощность зависит от размеров поперечного сечения. Приравняем нулю производную от передаваемой мощности (1.16) по переменной а, и при фиксированном значении b. Из уравнения найдем, что или . Это соответствует волновому сопротивлению линии равному 30 Ом. Для этого случая, принимая, что максимальное пробивное напряжение В/мм найдем оценку максимальной передаваемой мощности

при , Ом.

Коэффициент затухания электромагнитного поля в коаксиальной линии, вызванный конечной проводимостью металла, определяется соотношением

.

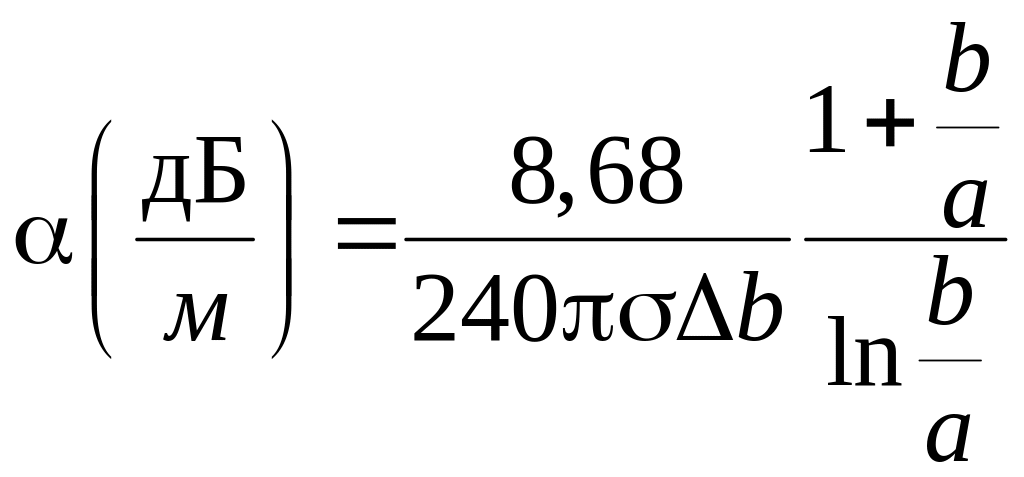Как видно, коэффициент затухания зависит от соотношения радиусов. При фиксированном значении b можно найти значение b/a, отвечающее минимуму затухания в линии. Обозначим и найдем условие минимума 

.

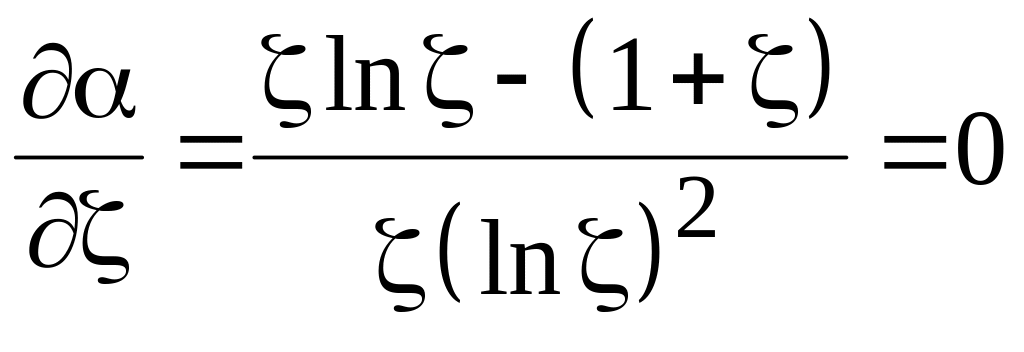Отсюда следует уравнение для

которое имеет решение . Это отношение радиусов соответствует волновому сопротивлению коаксиальной линии равному 77 Ом. Таким образом, минимальное затухание в коаксиальной линии определяется соотношениями

,

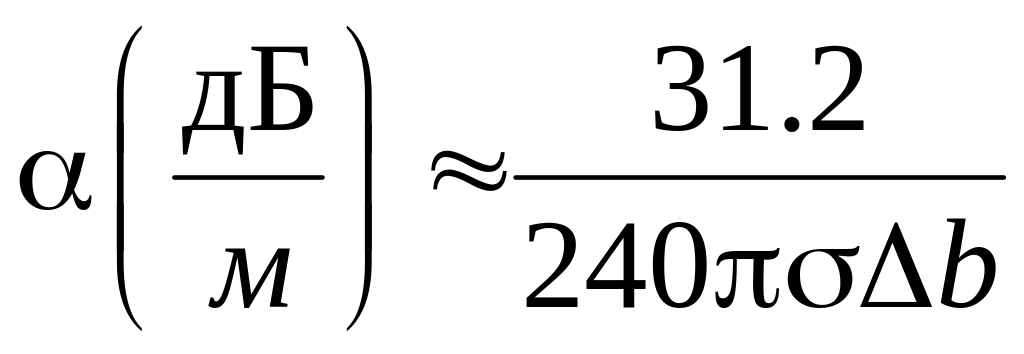при

.

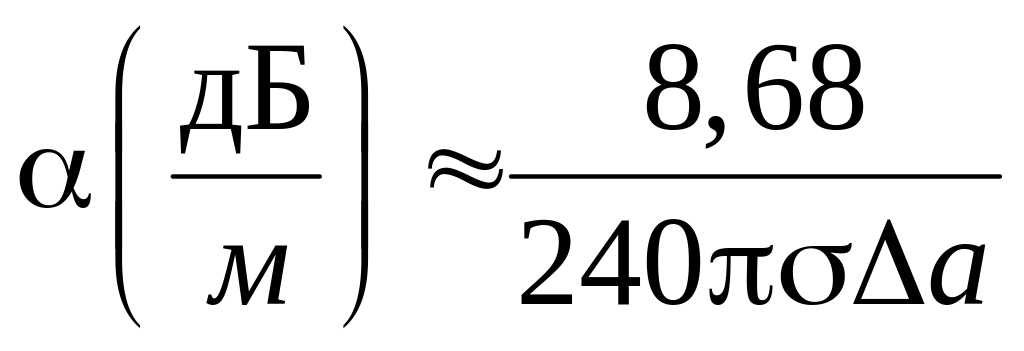С увеличением частоты затухание в коаксиальной линии монотонно возрастает и при сравнимых значениях высоты прямоугольного волновода и диаметра внутреннего цилиндра затухание в линии на частоте 10ГГц примерно в 2.5 раза выше, чем в волноводе. Размеры поперечного сечения коаксиальной линии определяются не только электродинамическими характеристиками, но и механической жесткостью конструкции.