4.2. Собственная добротность объемных резонаторов

Возможность существования электромагнитного поля на дискретных частотах возможно только при условии идеально проводящих стенок резонатора. Это в свою очередь означает, что собственное колебание, возникшее в резонаторе, будет существовать бесконечно долго. Очевидно, это противоречит закону сохранения энергии, согласно которому, энергия электромагнитного поля в замкнутом объеме должна релаксировать к нулю, обращаясь в тепловую энергию. Скорость релаксации энергии определяется собственной добротностью резонатора на резонансной частоте, определяемую как

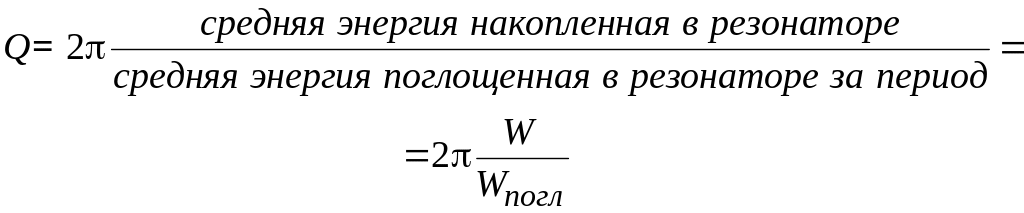. (4.9)

Множитель введен для окончательного упрощения вида формулы. Соотношение (4.9) можно преобразовать к иному виду, заменив поглощенную за период энергию, мощностью потерь через соотношение , где - период колебания на резонансной частоте . Поэтому (4.9) в эквивалентной форме есть

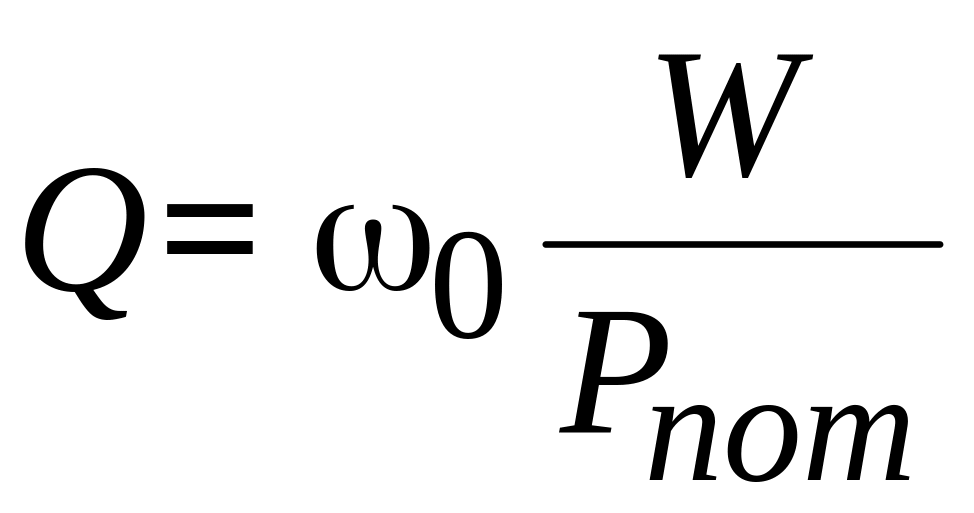. (4.10)

Согласно закону сохранения энергии, мощность потерь определяется скоростью уменьшения накопленной энергии, то есть

. (4.11)

Объединив (4.10) и (4.11) в общее соотношение, получим

.

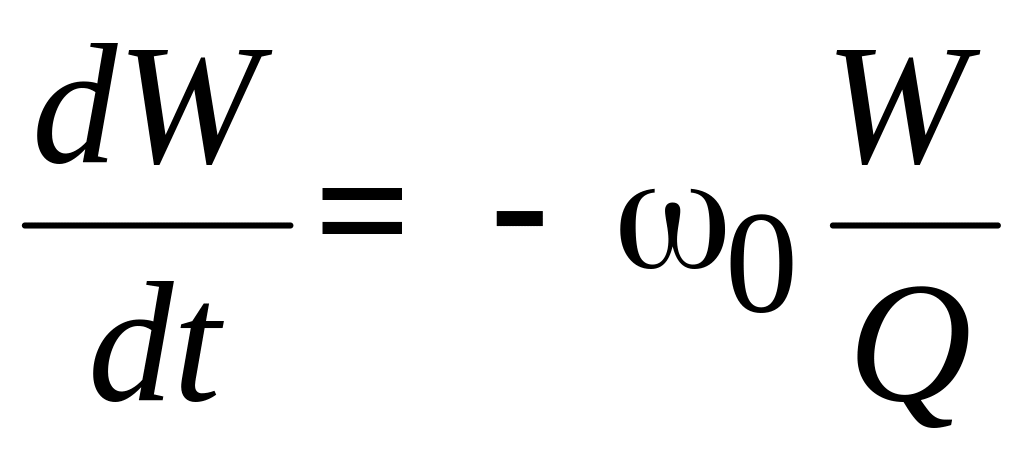Решение этого уравнения, определяет экспоненциальный спад накопленной энергии

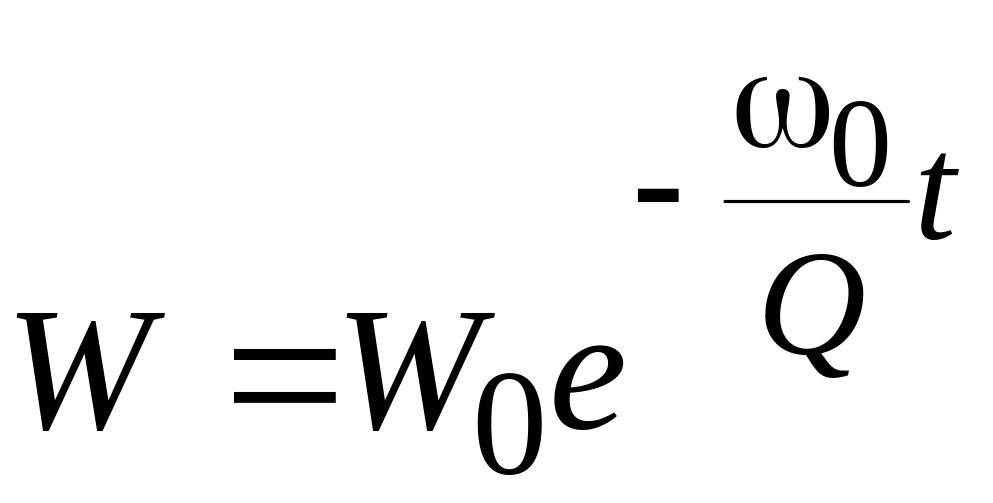. (4.12)

Электромагнитное колебание, возникшее на частоте резонанса, будет затухать по амплитуде. Квадратичная зависимость энергии от амплитуды колебания, позволяет представить напряженность электрического поля в резонаторе в соответствии с (4.12) в виде

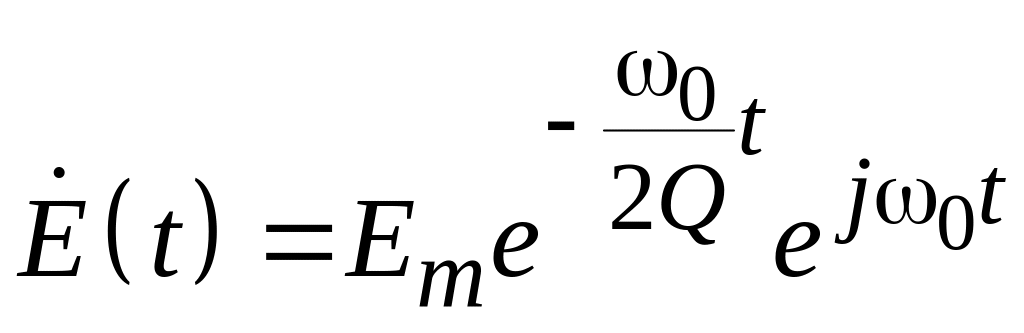. (4.13)

Колебание, непрерывно изменяющееся во времени, имеет спектральную плотность , которая вычисляется прямым преобразованием Фурье от . Таким образом

.

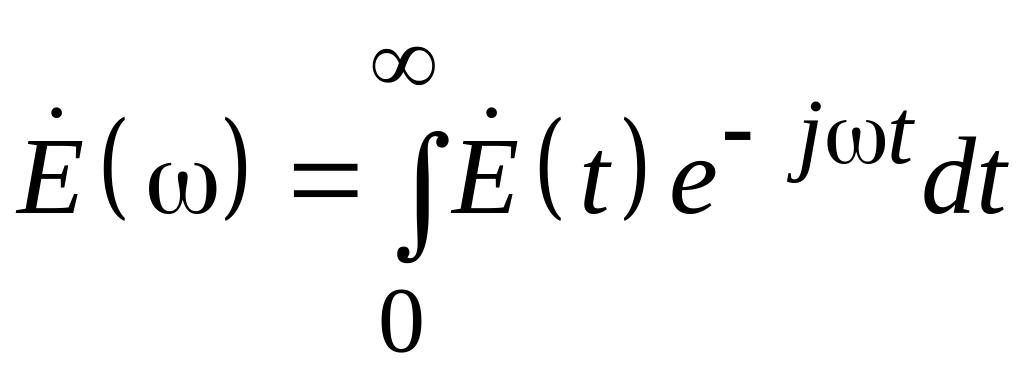Подставим в это соотношение (4.13), получим

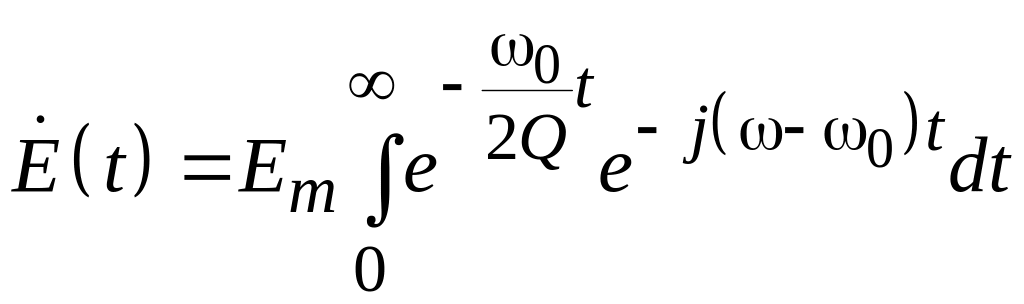. (4.14)

Интеграл в (4.14) вычисляется точно, поэтому

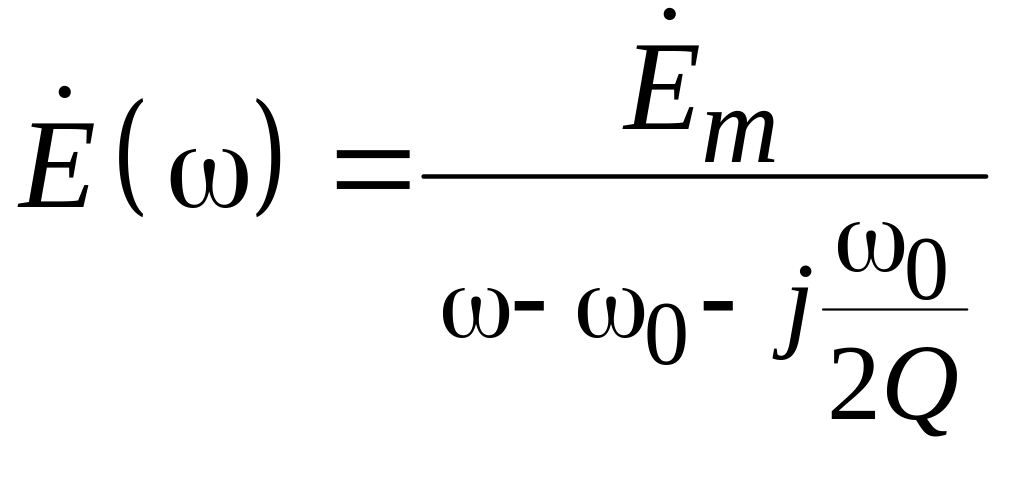. (4.15)

Следуя анализу резонансных систем, введем малую расстройку , как , где . Тогда (4.15) можно преобразовать к виду

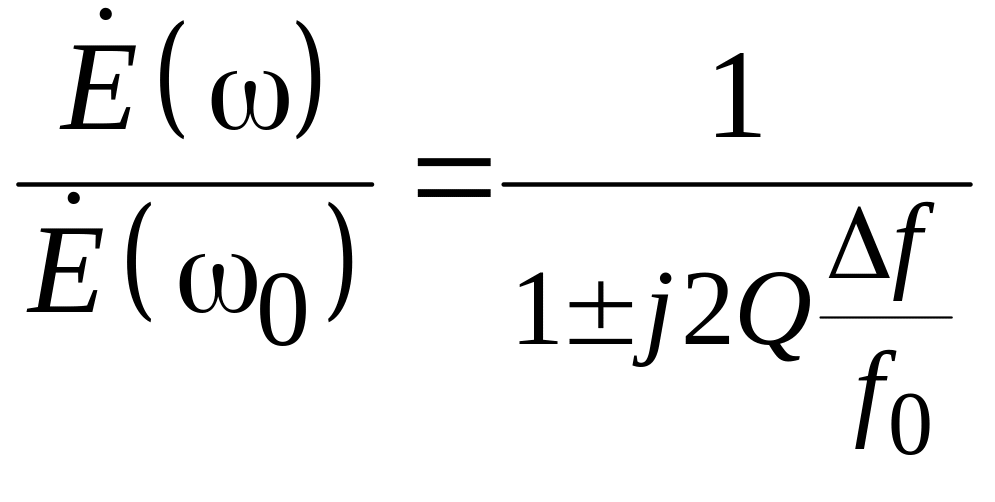, (4.16)

где 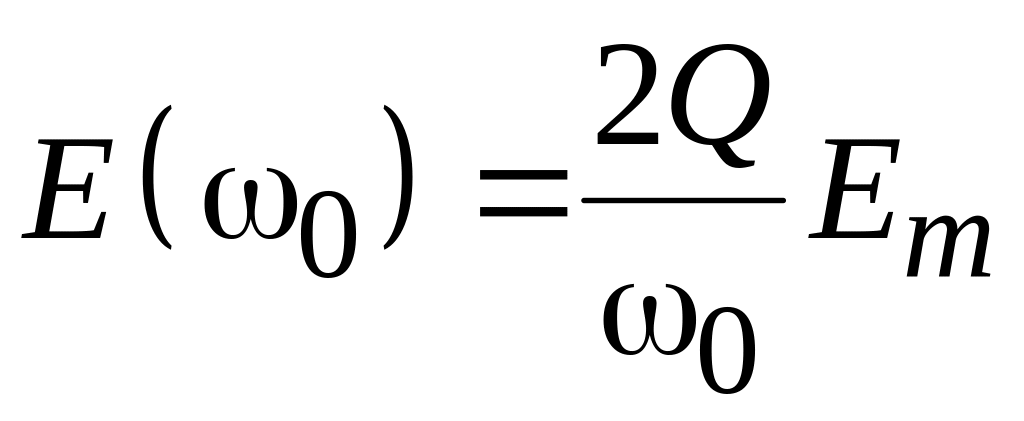- значение спектральной плотности на резонансной частоте.

Квадрат модуля соотношения (4.16) представляет нормированную частотную зависимость энергии накопленной в резонаторе. Из (4.15) найдем

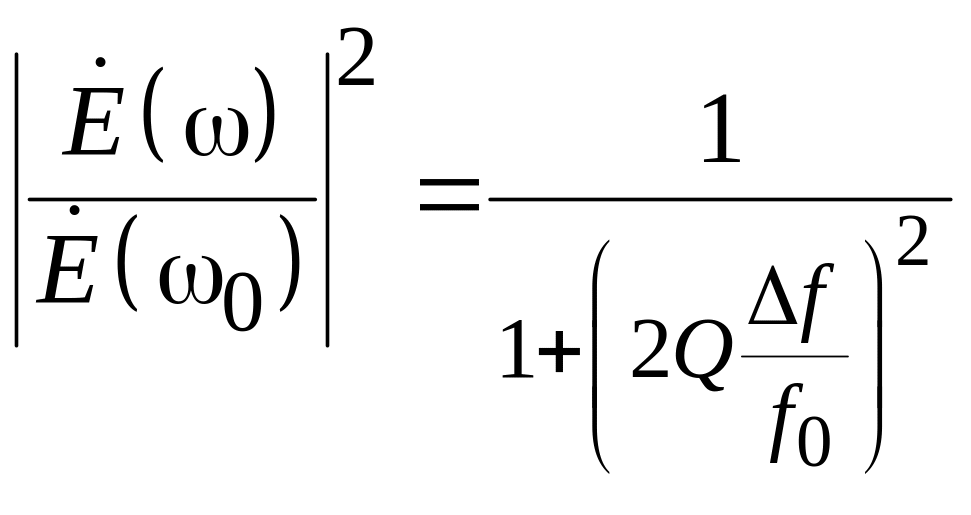. (4.17)

Соотношение (4.17) точно совпадает с частотной характеристикой LC колебательных контуров. Расстройка частоты соответствует спаду энергии до уровня равного . Полоса частот, соответствующая половинному спаду энергии равная называется полосой пропускания объемного резонатора.