3.2. Свойства матрицы рассеяния
Каждое уравнение в системе линейных уравнений (3.6) может быть представлено в виде
.
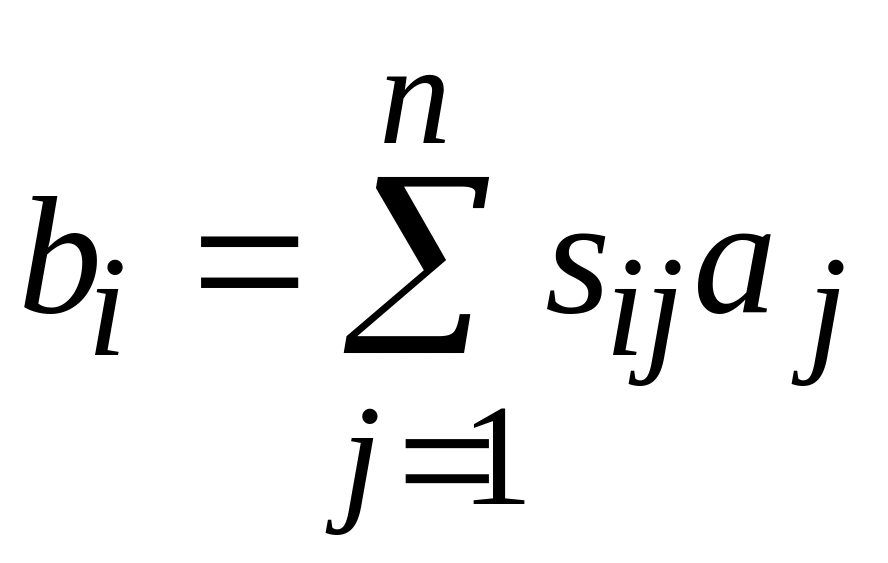(3.9)
Соотношение (3.9)
показывает, что рассеянная волна в i
– том плече многополюсника является
линейной комбинацией падающих волн.
Поэтому физический смысл элементов
матрицы рассеяния легко выявляется из
(3.9). Допустим, что источник электромагнитного
поля подключен к j
– тому плечу, а все остальные плечи
многополюсника согласованы с нагрузками.
Это означает, что
,
а во всех остальных плечах
.
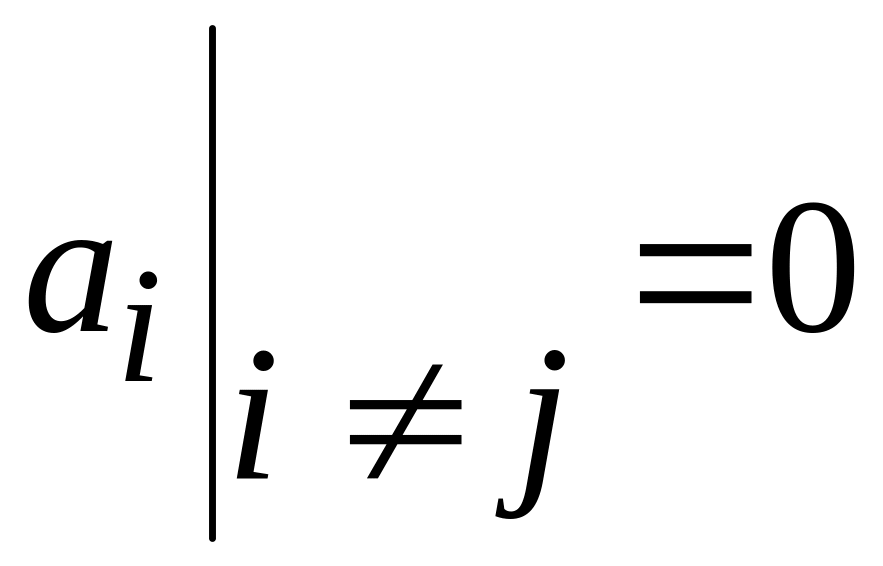Тогда из соотношения (3.9) следует, что
.
(3.10)
Отсюда очевидно, что
.
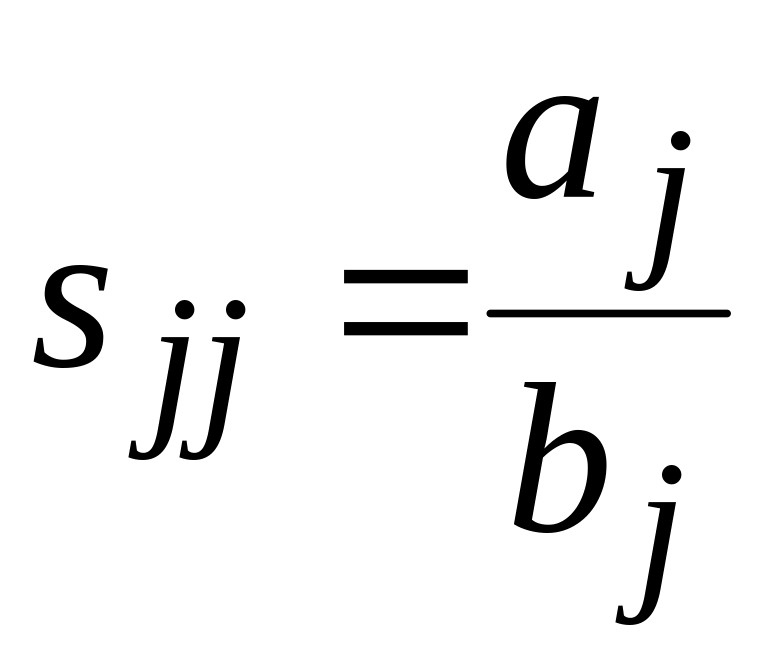(3.11)
В соответствии с
определением коэффициента отражения
из (3.11) следует, что
- коэффициент отражения по входу j
–того плеча, при условии, что остальные
плечи согласованы. Очевидно, что
в общем случае величина комплексная,
так как между падающей и рассеянной
волной возможен фазовый сдвиг. Таким
образом, на главной диагонали матрицы
рассеяния стоят коэффициенты отражения
по соответствующим плечам. Недиагональный
элементы определяют рассеянные волны
в i
– том плече при условии, что источник
поля включен в j
– тое плечо и все плечи согласованы.
При этом условии из (3.9) следует, что
.
(3.12)
Мощность рассеянной
волны в i
–том плече равна
.
В общем случае
комплексные величины. Поэтому, мощность
рассеянной волны в соответствии с (3.12)
равна
.
Квадрат модуля нормированной падающей
волны равен мощности в j
– том плече. Таким образом
определяет долю мощности, поступающей
из j
– того плеча в i
– тое плечо. Поэтому
можно считать коэффициентами связи
(передачи) между соответствующими
плечами.
Практический
интерес представляют волноводные
сочленения, обладающие пространственной
симметрией. Сочленение симметрично,
если оно переходит само в себя при
отражении от плоскости или при повороте
вокруг оси. Для симметричных сочленений
и матрица рассеяния (3.8) симметричного
2n
- полюсника
принимает вид
.
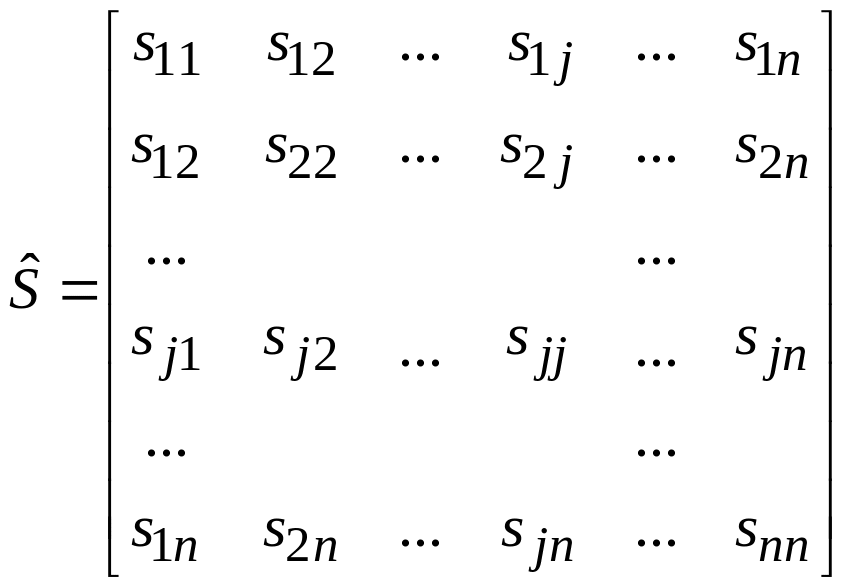(3.13)
Баланс мощностей в волноводном многополюснике при отсутствии в нем потерь, следуют из унитарности матрицы рассеяния. Матрица унитарна если
,
(3.14)
где
- единичная матрица.
Из (3.14) по правилу матричной алгебры следует, что
,
(3.15)
где i – номер строки, j – номер столбца.
Для симметричных сочленений соотношение (3.15) может быть представлено в виде:
суммы квадратов модулей элементов матрицы рассеяния по строкам (столбцам) равны единице
;
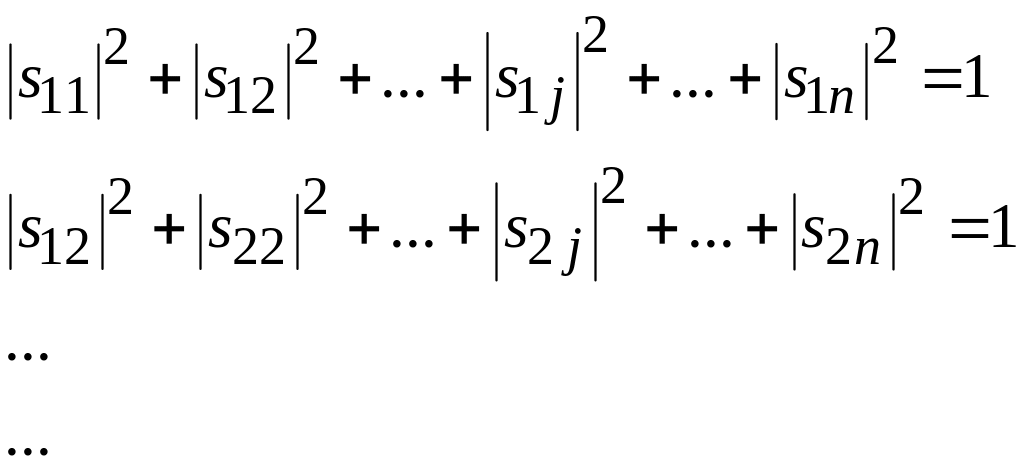(3.16)
суммы почленных
произведений строк (столбцов) элементов
матриц
и
равны
нулю
.
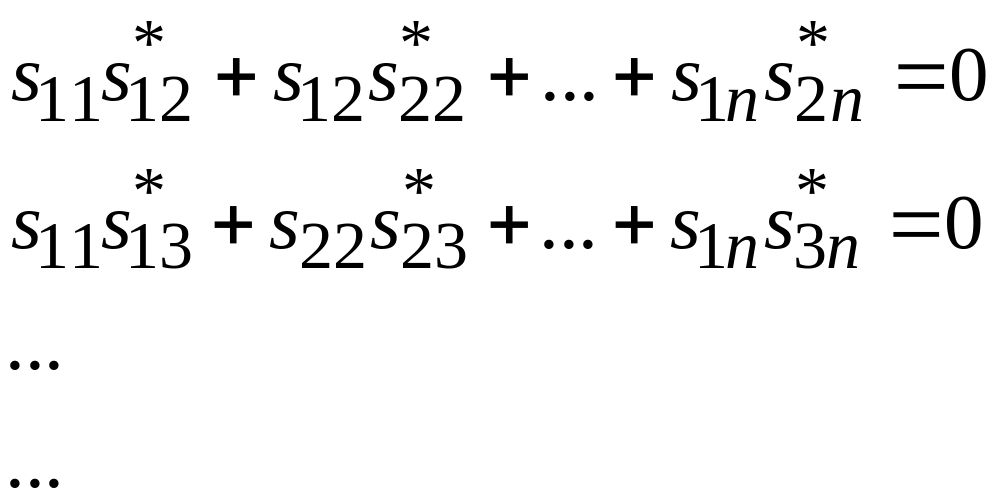(3.17)
Соотношение (3.16)
представляют собой уравнения баланса
мощности в многополюснике. При условии,
что единичная мощность поступает на
вход одного из плеч многополюсника,
мощность, прошедшая в многополюсник
делится между его плечами в соответствии
с уравнениями (3.16). Например, при
подключении источника поля к входу
первого плеча, мощность, прошедшая в
многополюсник равна
и из (3.16) следует, что
,
где слагаемые левой части пропорциональны мощностям во всех остальных плечах многополюсника.
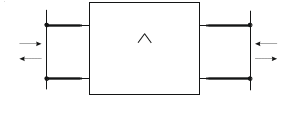В
заключении рассмотрим волновой
четырехполюсник как простейшее
многополюсное соединение. На рис. 3.2
изображен четырехполюсник с двумя
клеммными плоскостями 1, 2, одну из
которых считают входной, а другую
выходной. Падающие и рассеянные волны
в этих плоскостях обозначены
,
и
,
.
Линейная связь между ними, устанавливается
парой алгебраических уравнений, которые
в соответствии с (3.6) записываются в виде
.
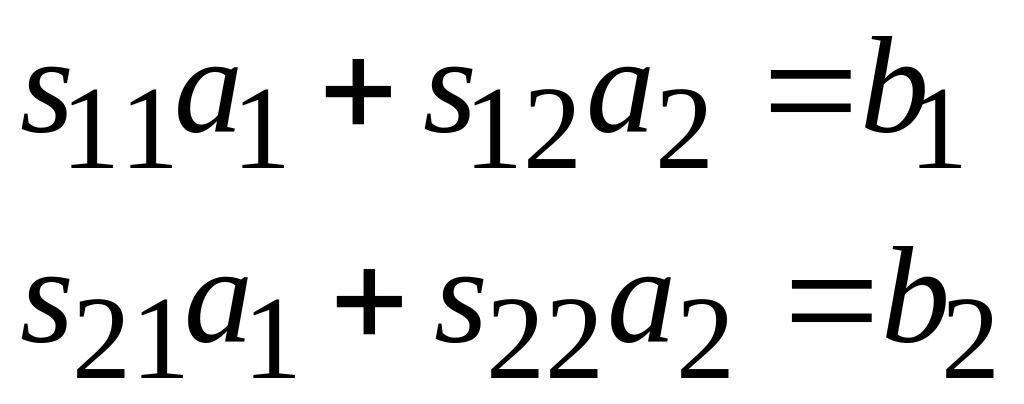(3.18)
У симметричных
четырехполюсников недиагональные
элементы равны
.
В отсутствии потерь матрица рассеяния
четырехполюсника унитарна и в соответствии
с (3.16), (3.17) элементы симметричной матрицы
рассеяния удовлетворяют уравнениям
,
.
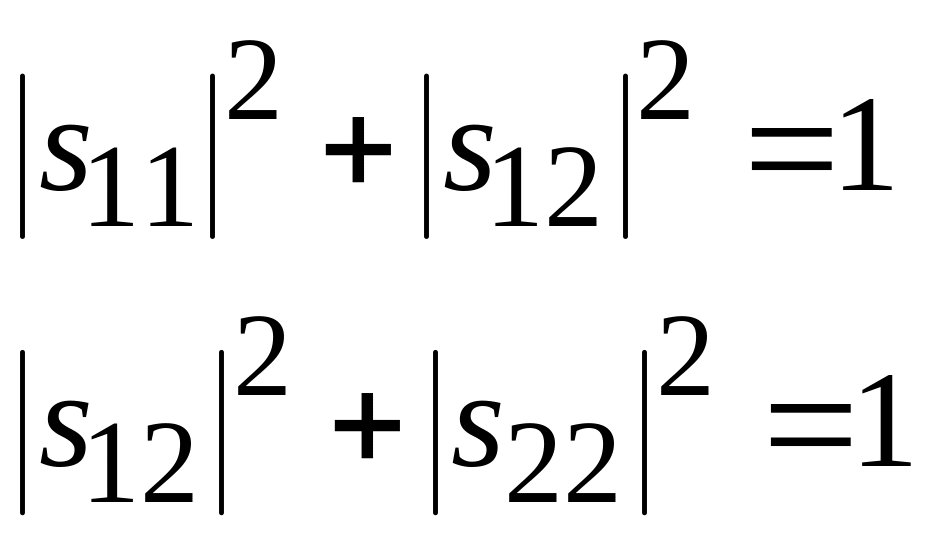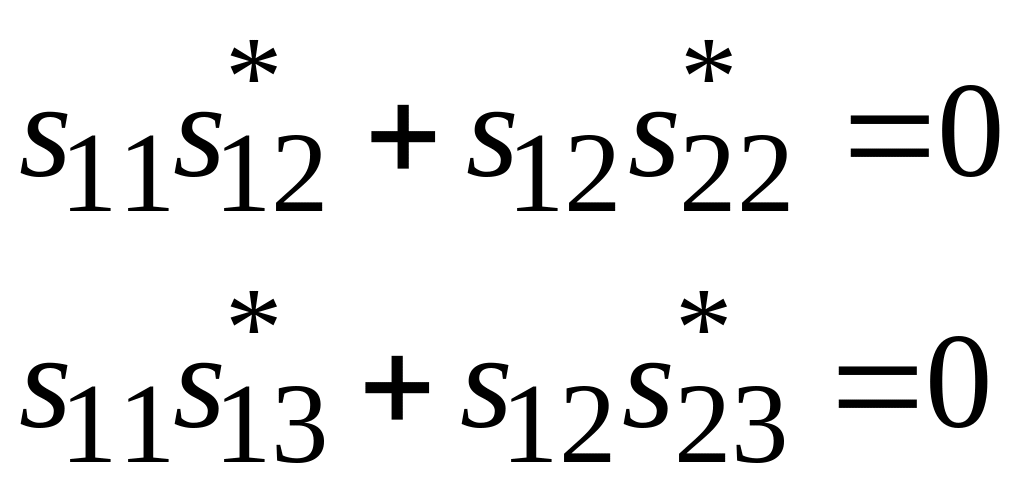(3.19)
И
з
(3.19) следует, что квадраты модулей
коэффициентов отражений в клеммных
плоскостях
.
Четырехполюсники могут соединяться каскадно. Для двух каскадно соединенных четырехполюсников рис. 3.3 входная волна второго четырехполюсника является выходной волной первого четырехполюсника. Изменив направления падающих и рассеянных волн второго четырехполюсника на противоположные, можно представить линейную связь между входными и выходными волнами в виде
.
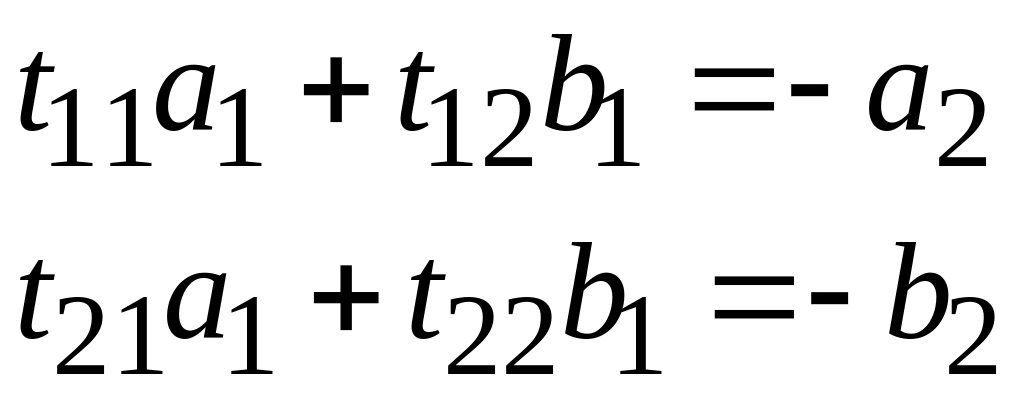(3.20)
Матрица системы уравнений (3.20) называется матрицей передачи четырехполюсника
.
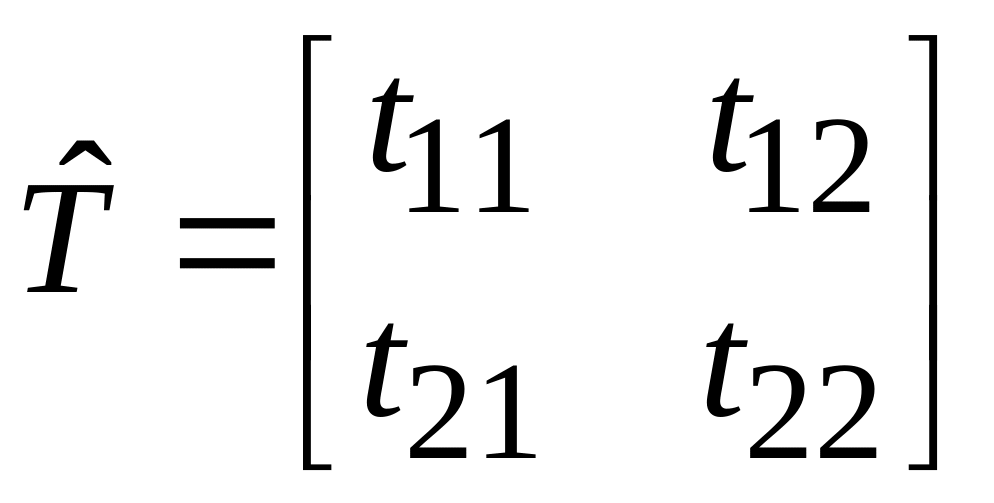Из (3.18) и (3.20) можно установить связь между элементами матриц рассеяния и передачи. Опуская подробности, запишем эти соотношения для симметричного четырехполюсника в окончательном виде
.
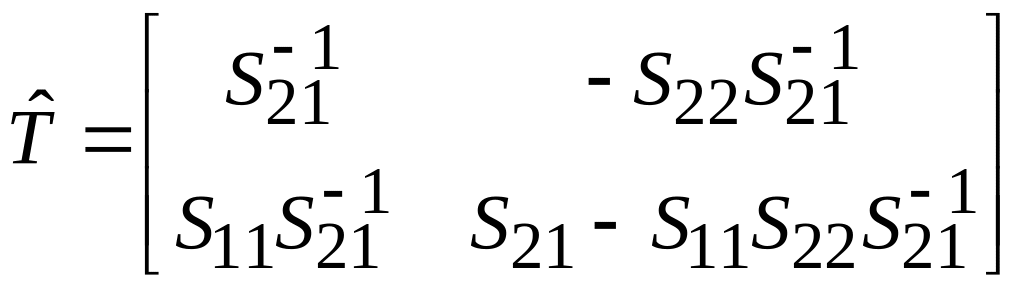Для каскадного соединения четырехполюсников, результирующая матрица передачи равна произведению матриц передачи отдельных четырехполюсников. Это имеет большое практическое значение при анализе цепей образованных каскадным включением четырехполюсников.