7.1.4 Длинная линия без искажений

Гармонический сигнал представляет собой лишь простейший вид переменных сигналов, передаваемых по линиям электропередачи. Часто оказывается, что форма передаваемого сигнала сложнее и сигнал может быть представлен суммой множества гармонических составляющих. При передаче такого сигнала вдоль длинной линии могут наблюдаться нелинейные искажения сигнала. Если амплитуда каждой из составляющих будет уменьшаться с различной интенсивностью, то возникнут так называемые амплитудные искажения, а если будут различаться временные сдвиги гармонических составляющих, то возникнут фазовые искажения.

Для того чтобы при передаче сигнала сложной формы посредством длинной линии отсутствовали нелинейные искажения достаточно, чтобы коэффициент затухания не зависел от частоты, а коэффициент фазы был бы прямо пропорционален частоте:

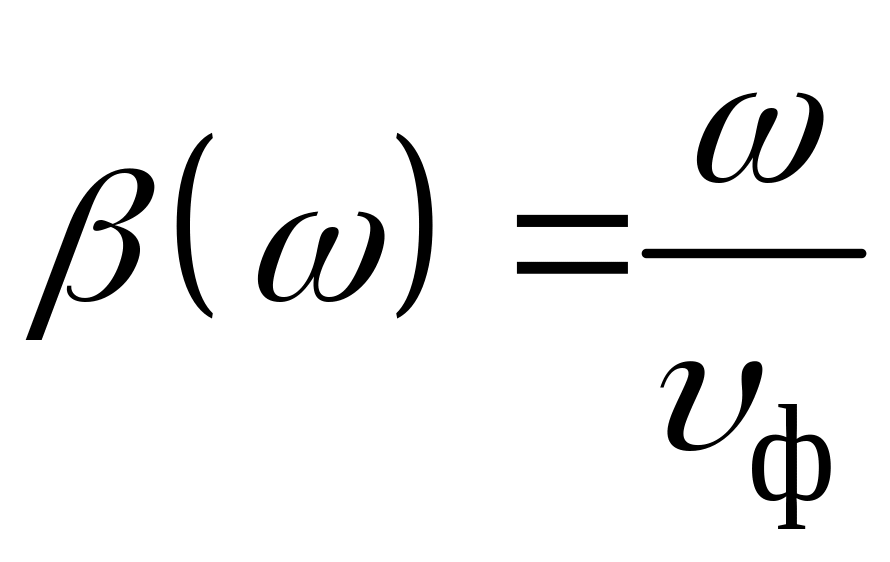, , (9)

где не зависит от частоты. Ограничения (9) представляют собой условия неискаженной передачи сигнала.

Данные условия будут автоматически выполняться, если для первичных параметров длинной линии справедливо соотношение¹:

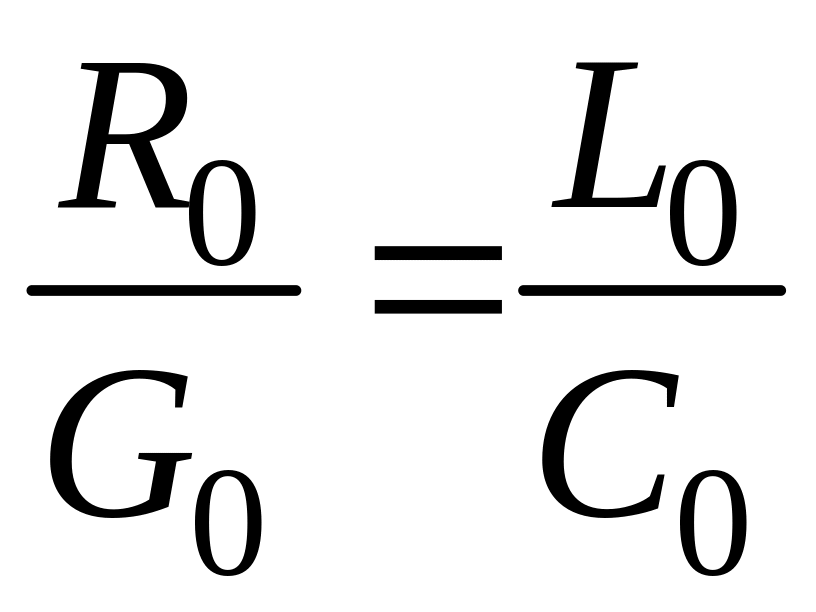. (10)

Действительно, в этом случае комплексный коэффициент распространения волны в линии:

(11)

Таким образом, коэффициент затухания равен и не зависит от частоты, а коэффициент фазы равен и прямо пропорционален частоте. Длинные линии, для которых выполняется условие (10) носят название линий без искажений.

На практике условие (10) без принятия специальных мер не выполняется и всегда:

. (12)

Для того чтобы неравенство (12) перешло в равенство (9) на практике, обычно, искусственно увеличивают параметр , включая через определенные промежутки в линию катушки индуктивности.

7.1.5 Анализ цепи, содержащей генератор гармонических колебаний, длинную линию и нагрузку

Рассмотрим задачу отыскания тока и напряжения в линии, нагруженной на конце на сопротивление нагрузки и подключенной к генератору гармонической ЭДС с внутренним сопротивлением (рис. 3).

Рис. 3 - Электрическая схема длинной линии, нагруженной с двух сторон

Обозначим через и значения напряжения и тока в сечении (сечение генератора), а через и - значения напряжения и тока в сечении (сечение нагрузки). Запишем систему уравнений, описывающих длинную линию прибавив к уже полученным ранее выражениям (4) и (5) для комплексных тока и напряжения в любом сечении линии закон Ома в комплексной форме для нагрузки и второй закон Кирхгофа в комплексной форме для цепи генератора:

(13)

Решим систему уравнений (13) относительно неизвестных констант интегрирования и , присвоив рассматриваемым сечениям координаты (для сечения генератора) и (для сечения нагрузки), где - длина линии.

Тогда из первого уравнения вытекает, что:

и .

Аналогично из второго уравнения получаем:

и .

Подстановка полученных выражений в третье и четвертое уравнение системы (13) дает:

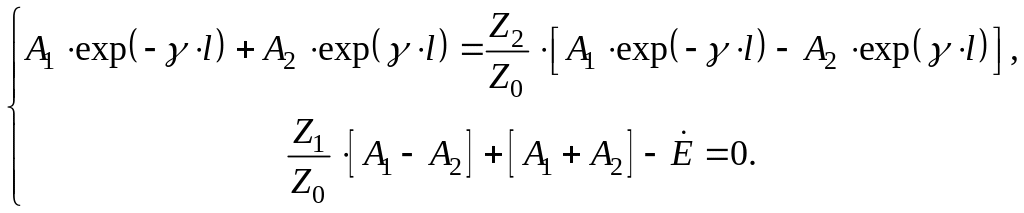(14)

Из первого уравнения системы (14) имеем:

, (15а)

а второе уравнение можно легко переписать в виде:

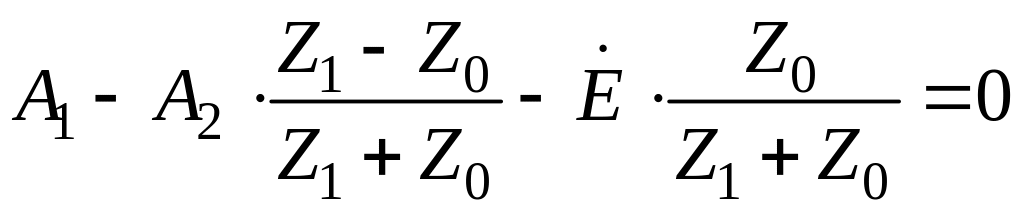. (15б)

Величина , являющаяся коэффициентом пропорциональности между комплексными амплитудами напряжения в падающей ( ) и отраженной ( ) волнах в сечении нагрузки называется комплексным коэффициентом отражения нагрузки, а величина , являющаяся коэффициентом пропорциональности между комплексными амплитудами напряжения в падающей и отраженной волнах в сечении генератора¹ носит название комплексного коэффициента отражения генератора.

Решая совместно полученные уравнения (15а) и (15б), находим, что:

, (16а)

. (16б)

Теперь выражения для тока и напряжения в любом сечении длинной линии принимают вид:

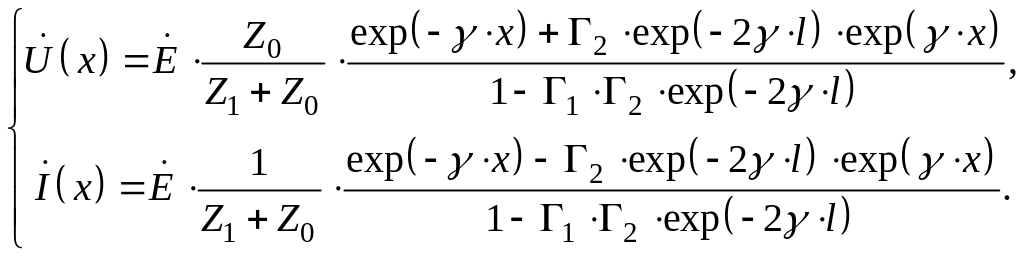(17)