
- •Вопрос 1. Что понимается под переходным процессом в электрической цепи? Какова его длительность? Чем обусловлены переходные процессы в электрических цепях? Существуют ли цепи, в которых их нет?
- •Вопрос 3. Классический метод анализа переходных процессов в эц.
- •Вопрос 4. Включение последовательной rl-цепи на постоянное напряжение
- •Определим свободную составляющую, решая оду
- •Вопрос 5. Включение последовательной rc-цепи на постоянное напряжение
- •Определим свободную составляющую:
- •Вопрос 5. Операторный метод анализа переходных процессов в эц.
- •Вопрос 6. В чем состоит преимущество операторного метода анализа электрических цепей перед классическим?
- •Вопрос 7. Прямое и обратное преобразование Лапласа и их применение для анализа электрических цепей
- •Линейность (сумма всех оригиналов есть сумма всех изображений)
- •Дифференцирование оригинала
- •Свертка
- •Предельные соотношения:
- •Вопрос 8. Характеристическое уравнение эц и метод его получения
- •Метод входного сопротивления (входной проводимости)
- •Метод главного определителя
- •Вопрос 9. Как определяется период свободных затухающих колебаний в последовательной и параллельной rlc – цепях?
- •Последовательная rlc – цепь
- •П араллельная rlc – цепь
- •Вопрос 10. Связь между операторной передаточной функции цепи и ее переходной характеристикой. Как ее получить, зная операторную передаточную функцию?
- •Вопрос 11. Анализ пп в нелинейных электрических цепях.
- •Вопрос 12. Анализ электрических цепей на основе метода переменных состояний.
- •Вопрос 13. Определить энергию мп в rl – цепи по истечении времени, длительностью в постоянную времени, принужденных ну.
- •Вопрос 14. Определить энергию эп в rc – цепи по истечении времени, длительностью в постоянную времени, принужденных ну.
Вопрос 4. Включение последовательной rl-цепи на постоянное напряжение
Этап 1.
|
Ток в индуктивности до коммутации:
|
|
Согласно I
закону коммутации:
–индуктивность заменяем разрывом.
|
Этап 2.
На основании законов Кирхгофа составим дифференциальное уравнение (этап № 2) относительно переменной тока в индуктивности по схеме после коммутации, описывающей мгновенные значения токов и напряжений.
С огласно
II з-ну Кирхгофа:
огласно
II з-ну Кирхгофа:
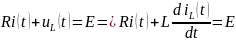 – НДУ
– НДУ
Решение в виде:

Определим свободную составляющую, решая оду
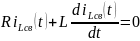
Из ОДУ получим характеристическое
уравнение (этап № 3), осуществляя
замену
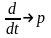 .
.
 ,
откуда
,
откуда
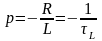 [c-1],
[c-1],
где
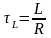 [c]
– постоянная RL-цепи.
[c]
– постоянная RL-цепи.
Знак «минус» в выражении указывает на то, что переходный процесс заканчивается и наступает установившийся режим.
Поскольку корень характеристического
уравнения отрицательный и вещественный,
то
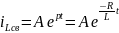 – свободная
составляющая (этап № 4) переходного
тока.
– свободная
составляющая (этап № 4) переходного
тока.
Определим принуждённую составляющую (1 способ). Поскольку внешнее воздействие является постоянным, т.е.
 ,
то решение для принуждённой составляющей
будем искать в виде:
,
то решение для принуждённой составляющей
будем искать в виде:
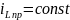
Осуществляя
подстановку последнего соотношения в
НДУ, получим:
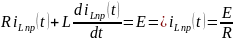
Определим принужденную составляющую тока в индуктивности
при t = ∞ (2 способ).

Индуктивность заменяем перемычкой.
На
основании закона Ома:
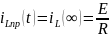 – конечное условие.
– конечное условие.
Таким образом, вид переходного тока в индуктивности определяется в виде:
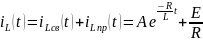
Определим const A (этап № 6), используя начальное условие
 .
.
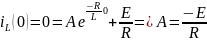
Переходные напряжения на индуктивности и резисторе:
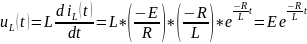
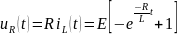

Постоянная времени последовательной
RL-цепи
графически определяется длиной
подкасательной кривой
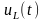 при любом значении
при любом значении
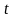 .
.
Вопрос 5. Включение последовательной rc-цепи на постоянное напряжение
|
Определим напряжение на емкости до
коммутации:
На основании II закона коммутации:
|
Составим дифференциальное уравнение цепи после коммутации:
По II закону Кирхгофа
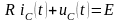 ,
отсюда
,
отсюда
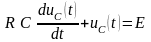 Полный вид решения:
Полный вид решения:
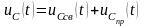 .
.Определим свободную составляющую:
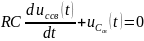
Характеристическое
уравнение
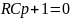 ,
=>
,
=>
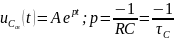
Принужденная составляющая при t = ∞
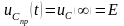 – конечное условие.
– конечное условие.
Общий
вид реакции:
 ,
где
,
где
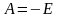 из начального условия
.
из начального условия
.
О кончательное
решение
кончательное
решение
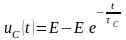 ,
,
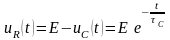 .
.
Построим графики соответствующих напряжений:
Вопрос 5. Операторный метод анализа переходных процессов в эц.
Определение постоянных интегрирования из начальных условий сильно осложняет расчёт переходных процессов классическим методом. По мере усложнения электрических схем и возрастания порядка дифференциальных уравнений трудности, связанные с нахождением постоянных интегрирования, увеличиваются. Для инженерной практики более удобным является метод решения линейных дифференциальных уравнений, при котором заданные начальные условия включаются в исходные уравнения и для нахождения искомых функций не требуется дополнительно определять постоянные интегрирования.
В прошлом столетии в
математике развивалось так называемое
символьное исчисление, построенное на
системе формальных операций над символом
«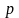 ».
Например, производная
».
Например, производная
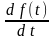 представлялась как результат действия
на функцию
представлялась как результат действия
на функцию
 символа «
».
В конце XIX
в. Английский инженер-электрик О. Хевисайд
успешно применил и развил
символический метод решения линейных
дифференциальных уравнений для расчёта
переходных процессов в электрических
цепях с сосредоточенными и распределёнными
параметрами.
символа «
».
В конце XIX
в. Английский инженер-электрик О. Хевисайд
успешно применил и развил
символический метод решения линейных
дифференциальных уравнений для расчёта
переходных процессов в электрических
цепях с сосредоточенными и распределёнными
параметрами.
В настоящее время операционное исчисление Хевисайда полностью вытеснено более общим и строгим методом – преобразованием Лапласа.
Идея этого метода заключается
в том, что из области функций действительного
переменного решение переноситься в
область функций комплексного переменного
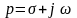 ,
где операции принимают более простой
вид, а именно: вместо исходных
дифференциальных или интегро-дифференциальных
уравнений получаются алгебраические
уравнения; затем полученный решением
алгебраических уравнений результат
«интерпретируется», т.е. производится
обратный переход в область функций
действительного переменного.
,
где операции принимают более простой
вид, а именно: вместо исходных
дифференциальных или интегро-дифференциальных
уравнений получаются алгебраические
уравнения; затем полученный решением
алгебраических уравнений результат
«интерпретируется», т.е. производится
обратный переход в область функций
действительного переменного.
Преобразованием Лапласа
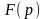 функции
является функция комплексной переменной
вида:
функции
является функция комплексной переменной
вида:
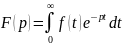
Существует обратное преобразование Лапласа:
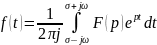
Перечислим основные свойства преобразования Лапласа:
Линейность (cумма всех оригиналов есть сумма всех изображений)
Если
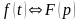 ,
то
,
то
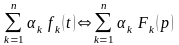 .
.
Дифференцирование оригинала
Если
,
то
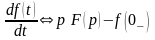 .
.
Интегрирование оригинала сводится к делению изображения на р
Если
,
то
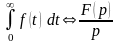 .
.
Сжатие (теорема подобия)
Если
,
то
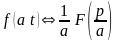 .
.
Запаздывание
Если
,
то
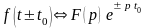 .
.
Смещение
Если
,
то
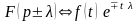 .
.
Свертка
Если
,
то
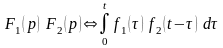 .
.
Предельные соотношения:
 .
.
Оригинал функции можно найти и с помощью теоремы разложения.
Если изображение функции представлено в виде дроби
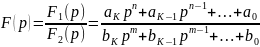 ,
,
причем многочлены (относительно р) F1(p) и F2(p) удовлетворяют следующим условиям:
степень
 ниже
степени
ниже
степени
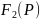 ,
,
ак и bk – вещественные числа,
то
оригинал находим по формуле
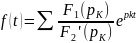 ,
где
,
где
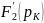 –
значение производной при р = рк,
–
значение производной при р = рк,
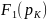 –
значение числителя при р = рк.
–
значение числителя при р = рк.
В том случае, если один из корней равен нулю, то
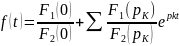
Последовательность расчета переходных процессов операторным методом заключается в следующем.
1. Находят независимые начальные условия – ток на катушке индуктивности iL(0) и напряжение на конденсаторе uC(0) в момент коммутации.
2. Составляют операторную схему замещения. Помня при этом,
операторная схема сохраняет конфигурацию послекоммутационной электрической цепи;
активные сопротивления переносятся в операторную схему без изменения;
индуктивность L заменяется элементом pL последовательно, с ним включается добавочная эдс, которая направлена по току. Величина добавочной ЭДС равна LiL(0);
емкость C заменяется элементом
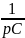 ,
после которого последовательно
включается добавочная эдс, равная
,
после которого последовательно
включается добавочная эдс, равная
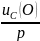 и направленная против
направления тока;
и направленная против
направления тока;Если задача имеет нулевые независимые начальные условия uС(0)=0, iL(0)=0, то добавочные ЭДС в операторную схему не включаются.

3. Используя любой известный метод расчета электрических цепей (метод непосредственного применения законов Кирхгофа, метод контурных токов и т. д.), определяют изображения токов I(p) для операторной схемы.
Законы Кирхгофа в операторной форме:
–
алгебр. сумма изображений токов в узле
равна нулю:
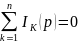
–
алгебр. сумма изображений напряжений
в замкнутом контуре равна нулю: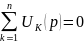
4. Изображение напряжения на любом из элементов цепи находим по закону Ома в операторной форме:
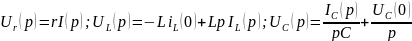
5. От изображения токов I(p) и напряжений U(p) переходим к их оригиналам i(t) и u(t).
Операторный метод удобен при расчете сложных электрических цепей.
При применении этого метода можно пользоваться всеми методами расчета электрических цепей.
При ненулевых начальных условиях, пользуясь методом наложения, можно сначала решить задачу для нулевых начальных условий, а затем на полученные результаты наложить те результаты, которые получаются только от действия дополнительных источников энергии.
Символический метод можно применять лишь к гармоническим функциям, операторный метод обладает значительно большей общностью и применим к широкому классу функций.


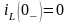 ,
поскольку ключ разомкнут.
,
поскольку ключ разомкнут.
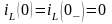


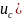
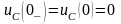 .
.