Лекции По Физике Оптике Для Дневников (Переверзев В. Г
.).pdf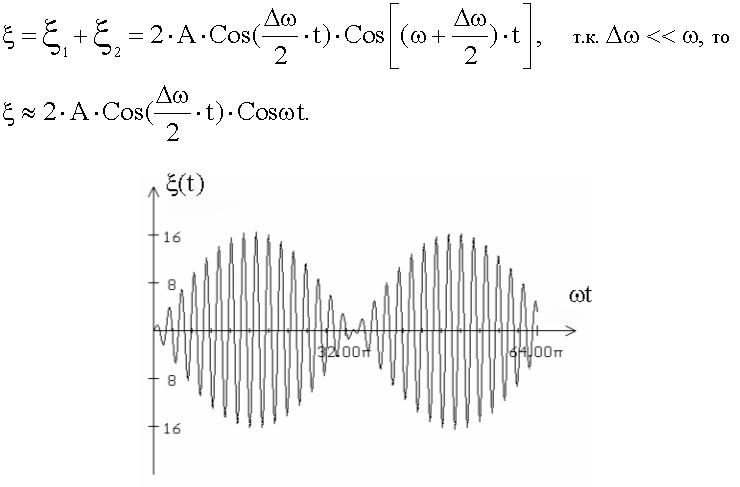
График результирующего колебания - график биений, т.е. почти гармонических колебаний частоты ω, амплитуда которых мед-
ленно меняется с частотой Δω.
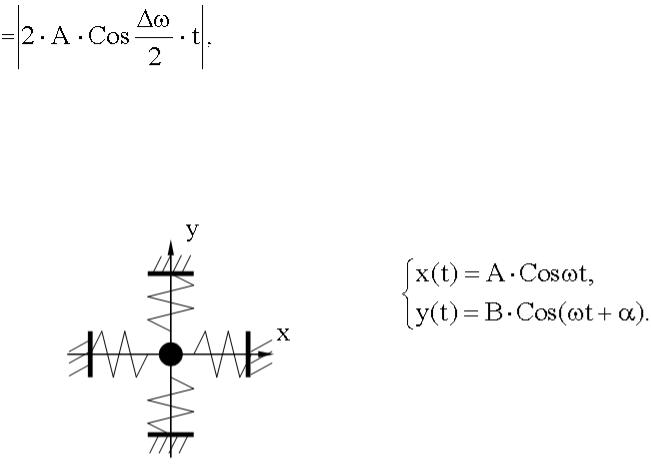
Амплитуда из-за наличия знака модуля (амплитуда всегда > 0) частота с которой изменяется амплитуда, равна не Δω / 2, а в два раза выше - Δω.
14.3.4. Сложение взаимно-перпендикулярных колебаний
Пусть маленькое тело колеблется на взаимно-перпендикулярных пружинках одинаковой жесткости. По какой траектории будет двигаться это тело?
Это уравнения траектории в параметрическом виде.
Для получения явной зависимости между координатами x
и y надо из уравнений исключить параметр t.
Из первого уравнения:
; 
.
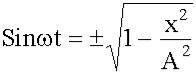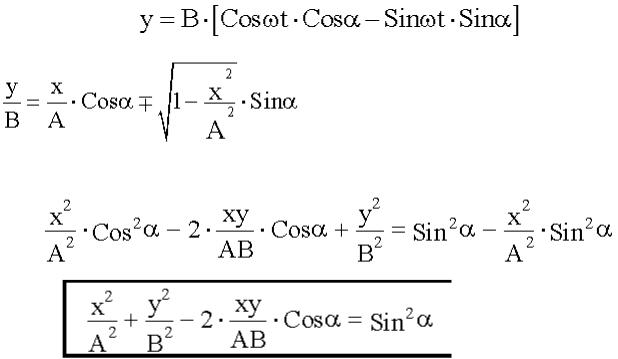
Из второго:
.
После подстановки: |
. |
Избавимся от корня: |
|
.
- это уравнение эллипса.
Частные случаи:
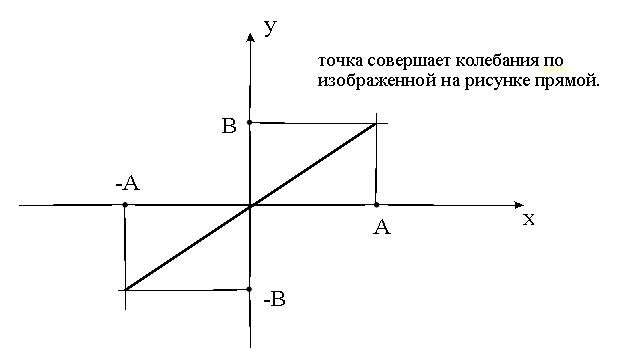
1. 
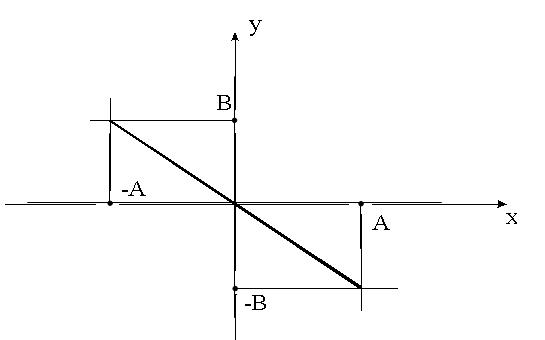
2. 
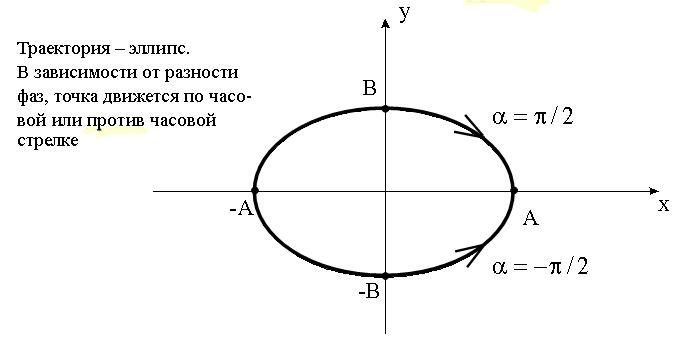
3. 
14.4. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Рассмотрим колебания, происходящие в двух системах:
а) колебания заряда в колебательном контуре L,C, имеющем активное сопротивление R;
б) колебание грузика, прикрепленного к пружинке, учтем влияние трения на движение грузика.
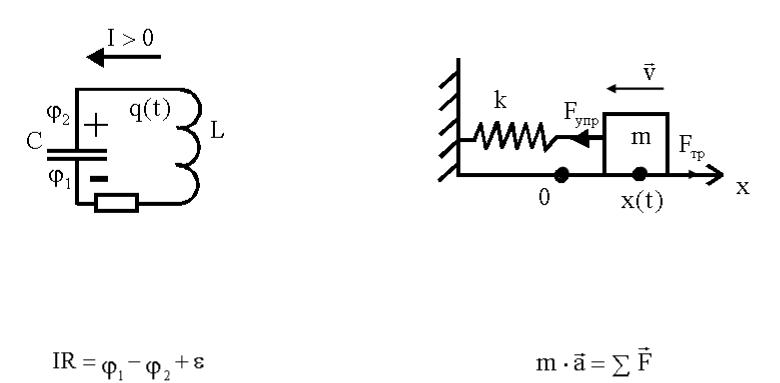
14.4.1. Колеблющиеся системы
14.4.2. Законы движения
Закон Ома для неоднородного участка цепи (10.7): |
Второй закон Ньютона (4.6): |
14.4.3. Применение законов движения, с учетом особенности наших систем
Или, используя другое обозначение производной:
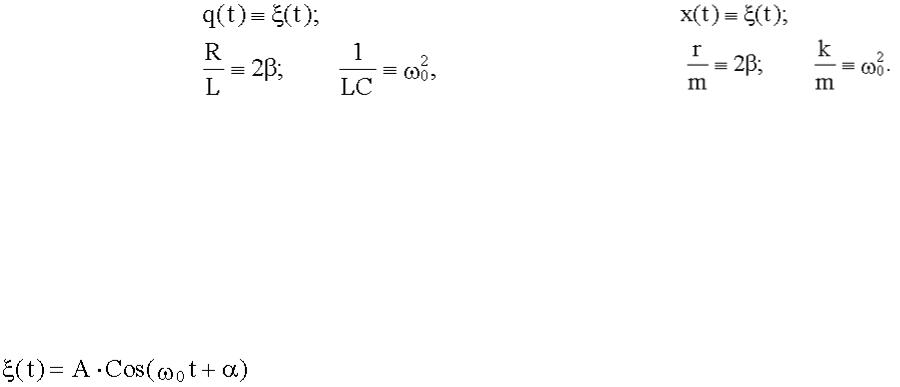
14.4.4. Введем обозначения:
14.4.5. Дифференциальное уравнение, описывающее затухающие колебания наших двух систем в этих обозначениях будет иметь один и тот же вид
.
14.4.6. Решение
Каким будет его решение? При 
(отсутствие сопротивления, трения) оно должно переходить в
(см. 14.2).
Наличие затухания, потерь энергии, переход ее из электромагнитной или механической в тепловую приведет к уменьшению амплитуды колебаний с течением времени, станет другой, меньшей чем ω0, и частота колебаний.
Предположим, что амплитуда убывает по экспоненциальному закону, т.е. A(t) = A0·e-βt(e=2,71828...),
тогда решение будем искать в виде:
.
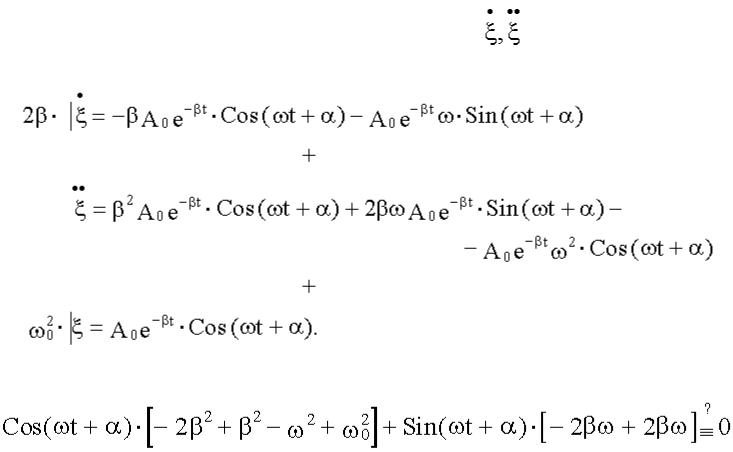
14.4.7. Проверка
Выясним, при каких условиях эта функция будет решением, для этого найдем |
и подставим в дифференциальное уравне- |
ние. |
|
Сгруппируем члены с косинусом и синусом, на A0e-βt сократим:
.
Для тождественного обращения левой части в ноль надо, что бы коэффициент при косинусе обращался в ноль (коэффициент
при синусе обратился в ноль, т.к. мы "удачно" выбрали A(t) = A0-βt). Из этого требования следует выражение для - ωчастоты затухающих колебаний.