Лекции По Физике Оптике Для Дневников (Переверзев В. Г
.).pdf
.
Таким образом, амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определен-
ной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота - ωрез - резонанс-
ной. Для определения ωрез исследуем функцию A(ω) на максимум, для этого достаточно найти минимум знаменателя у выра-
жения A(ω). Возьмем от него производную по и приравняем к нулю:
,
откуда:
.
При 2β2 > ω20 резонанс отсутствует ( ωрез - мнимое число).
14.5.6.1.2.1. Амплитуда при резонансе
Амплитуда при резонансе получается при подстановке найденного выражения ωрез в формулу для A(ω).
.
При β << ω0:
.
При ω = 0 отклонение системы от положения равновесия
.
Найдем отношение Aрез / A0при условии β << ω0:
,
здесь Q - добротность.
Добротность показывает (при β << ω0 ) во сколько раз амплитуда при резонансе больше смещения при ω = 0.
14.5.6.1.2.2. Резонансные кривые
График зависимости A(ω)при различных β носят название резонансных кривых.
β1 < β2 < β3, 2β23 > ω20, в этом случае резонанса нет.
15.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
15.1.1. Что такое упругая волна?
Упругая волна - это процесс распространения колебаний в упругой среде. Характерное свойство волны - перенос энергии без переноса вещества.
15.1.2. Описание волны
Для описания волны надо ввести функцию, в общем случае - векторную, задающую смещение от положения равновесия каждой
частицы упругой среды для любого момента времени. Обозначим эту функцию греческой буквой 
[кси]. Аргументами ее, в
соответствии с вышесказанным, будут три пространственные переменные - x, y, z, задающие положение частицы (или радиус-
вектор 
), и время t, т.е.
.
15.1.3. Скорость движения частиц упругой среды
- это частная производная от смещения по времени, т.е.
,
с такой скоростью частицы среды колеблются около своих положений равновесия.
15.1.4. Продольные и поперечные волны
Обозначим через 
скорость распространения волны. Если направление смещения 
(и скорость частицы 
) совпадают с направлением скорости волны, то волна называется продольной. Если 
и 
взаимно перпендикулярны, то волна поперечная.
15.1.5. Фронт волны
- поверхность, отделяющая часть пространства, охваченную волновым процессом, от той части, где колебания не возникли.
15.1.6. Волновая поверхность
- это геометрическое место точек, колеблющихся в одинаковой фазе.
15.1.7. Плоская и сферическая волны
Плоская волна - волновые поверхности - плоскости. Сферическая волна - волновые поверхности - сферы. В общем случае форма волновых поверхностей может быть любой.
15.1.8. Длина волны
- это расстояние, на которое распространяется волна за один период колебаний.
см. (3.9),
Так как (14.1.1.3) |
, |
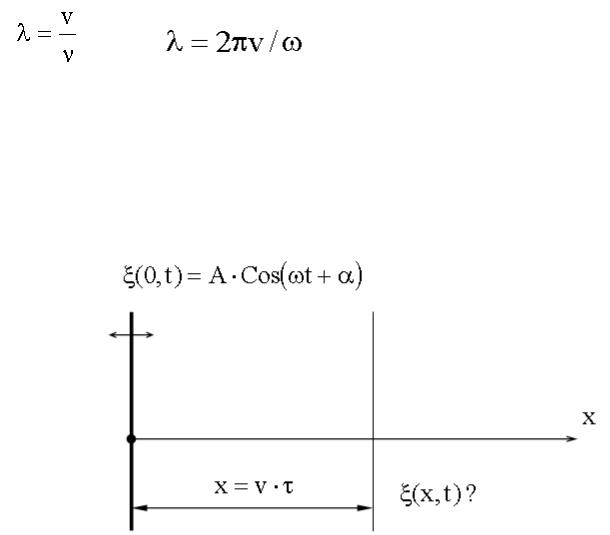
то |
или |
. |
15.2. УРАВНЕНИЕ ПЛОСКОЙ ВОЛНЫ.
Пусть в начале координат находится твердая плоскость, которая колеблется по гармоническому закону и вынуждает частицы упругой среды, находящейся рядом с ней, колебаться по этому же закону. Направим ось x перпендикулярно этой плоскости.
Тогда вдоль этой оси будет распространяться плоская гармоническая продольная волна. Наша задача - найти 
- уравне-
ние волны, если задано 
.
Колебания до волновой поверхности, удаленной от начала координат на расстояние x, дойдут через время 
, значит уравнение волны
.
15.2.1. Фаза волны
- это аргумент у косинуса в уравнении волны, т.е.
,
Фаза плоской волны зависит от двух переменных - x и t.
15.2.2. Фазовая скорость
- это скорость перемещения в пространстве поверхности, вдоль которой фаза волны (15.2.1) остается постоянной, т.е.
.
Найдем производную от этого выражения по времени:
,
откуда искомая фазовая скорость волны:
.
15.2.3. Уравнение плоской волны,
распространяющейся в направлении, противоположном оси x:
.
Из (15.2.2) для этой волны:
.
15.2.4. Волновое число, симметричная форма уравнения волны
.
Введем
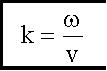- волновое число.
Тогда
.
При такой записи координата х и время tвходят в уравнение волны симметрично.
15.2.4.1. СВЯЗЬ ВОЛНОВОГО ЧИСЛА С ДЛИНОЙ ВОЛНЫ
.
15.2.5. Уравнение плоской волны, распространяющейся в произвольном направлении. Волновой вектор
,
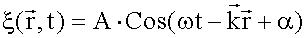здесь 
- волновой вектор,
- скалярное произведение волнового вектора и радиус-вектора.
15.3. ВОЛНОВОЕ УРАВНЕНИЕ
Применяя второй закон Ньютона (4.6) к упругой среде, можно получить дифференциальное уравнение в частных производных, решением которого будет уравнение волны. Логическая схема этого вывода такова:
15.3.1. Вывод закона Гука для бесконечно малого упругого стержня
Выделим элемент упругого стержня, длиной Δx.