Площадь поверхности вращения

Площадь поверхности, образованной вращением кривой , вокруг оси Ох находится по формуле:

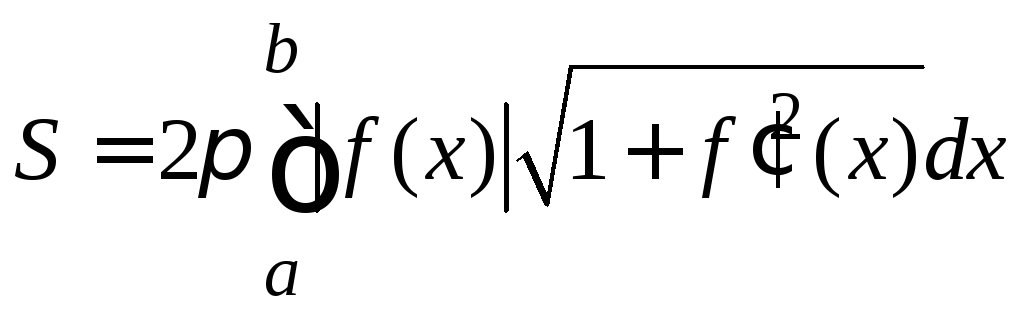
Докажем эту формулу методом дифференциала.

Пусть линия, которая является графиком непрерывно дифференцируемой на функции, вращается вокруг осиОх. Найдём площадьповерхности, образованной вращением дуги этой кривой для

Через произвольную точку , проведём плоскость перпендикулярную оси вращенияОх.Дадим аргументуприращениеЧерез точку, принадлежащую, также проведём плоскость, перпендикулярную осиОх.

Найдём дифференциал площади поверхности вращения , рассматривая поверхность между двумя сечениями, как элементарное кольцо.развернув его, получим полоску ширинойи длиной, так как- радиус кольца.

dl

Площадь этого прямоугольничка . Так как дифференциал дуги, то.

Интегрируя полученное равенство в пределах от до, приходим к нашей формуле

Площадь поверхности, образованной вращением вокруг осиОхкривой, заданной параметрически:

Так как дифференциал дуги в этом случае , то. Проинтегрировав поотдо, получаем формулу для вычисления площади поверхности вращения вокруг осиОхкривой, заданной параметрически.

29. Пример 29

Найти площадь поверхности вращения дуги синусоиды

Решение. по формуле для вычисления поверхности вращения вокруг осиОхкривой,:

Статические моменты и центр тяжести плоской кривой

Статическим моментом материальной точки, находящейся в плоскости Охy, относительно координатной оси Ох(илиОy)называется произведение массы этой точки на её ординату (соответственно абсциссу). Статическим моментом системы точек относительно координатной оси называется сумма статических моментов всех точек системы относительно этой оси.

Пусть на плоскости Охyзадана система материальных точексоответственно с массами.

Статическим моментом системы материальных точек относительно осиОхназывается сумма произведений масс этих точек на их ординаты (т.е. на расстояния этих точек от осиОх):.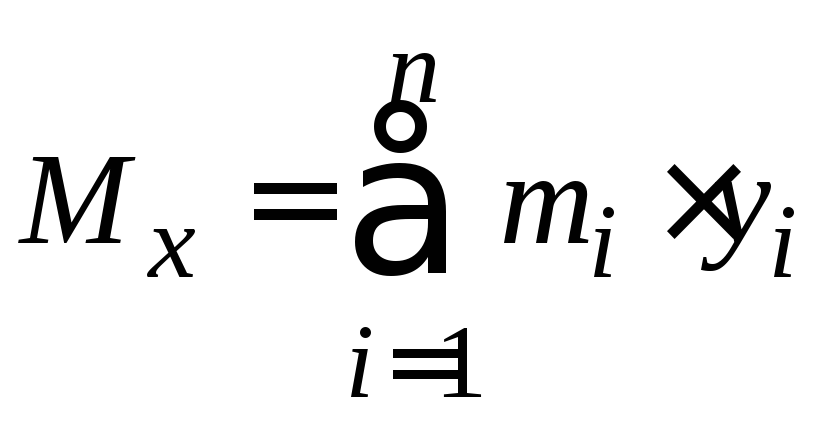

Аналогично определяется статистический моментэтой системы относительно оси:.

Пусть массы распределены непрерывным образом вдоль некоторой кривой, тогда выразим статический момент через определённый интеграл для чего используем метод дифференциала.

Пусть - это уравнение материальной кривойАВ. Будем считать её однородной с постоянной линейной плотностью.

Для произвольного на кривойАВнайдётся точка с координатами. Выделим на кривой элементарный участок длины, содержащий точку. Тогда масса этого участка равна. Сосредоточим массу дугив одной точке, отстоящей от осина расстоянии. Тогда дифференциал статического момента("элементарный момент") будет равен. т.е..

Отсюда следует, что статический момент кривойАВотносительно осиОхравен .

Аналогично находим :

.

С помощью статическихе моментов и дуги кривой определим положение её центра тяжести (центра масс).

Центром тяжести системы материальных точек с массаминазывается точкаС, обладающая тем свойством, что если в ней сосредоточить всю массу системны, то её статический момент по отношению к любой координатной оси будет равен статическому моменту системы точек относительно той же оси. Обозначим черезцентр тяжести кривой AB.

Из определения центра тяжести следуют равенства ,илии. Отсюда,

или ;.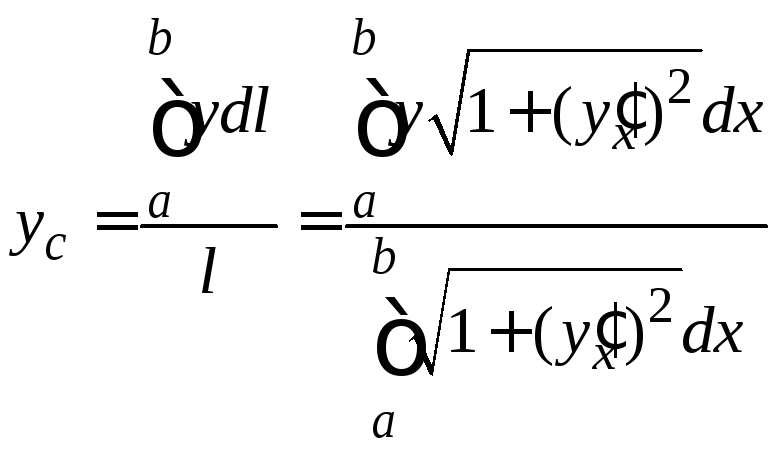