Площади плоских фигур.

Разобьём площадь трапеции на элементы (полоски) с основанием и высотой. Площадь одного такого элемента (отбрасывая бесконечно малые высшего порядка) равна

– элемент площади в прямоугольных координатах.

Интегрируя равенство в пределах от донайдём площадь криволинейной трапеции.

Если на, то

Итак, мы применили здесь метод дифференциала, сначала составив дифференциал искомой величины, а затем путём интегрирования нашли значение самой величины.

Площадь плоской фигуры, заданной условиями

находится по формуле

Для криволинейной трапеции вида

Площадь плоской фигуры, ограниченной кривой, заданной в параметрической форме:

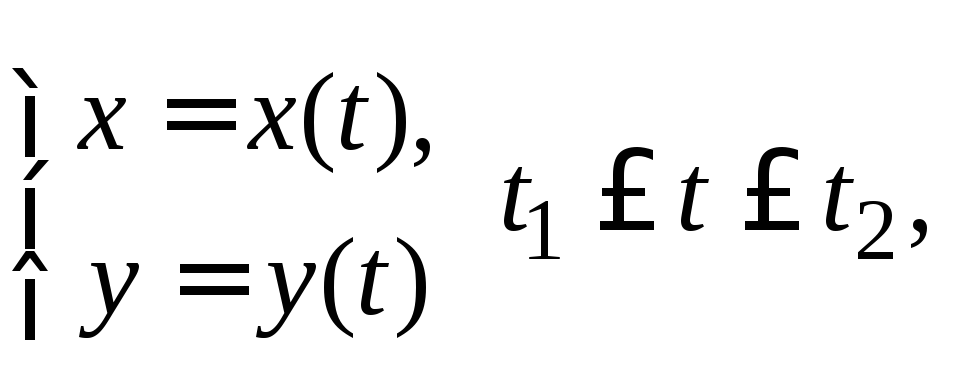
вычисляется по формуле:

ч.т.д.

Если непрерывная кривая задана в полярных координатах, то площадь криволинейного сектора

S

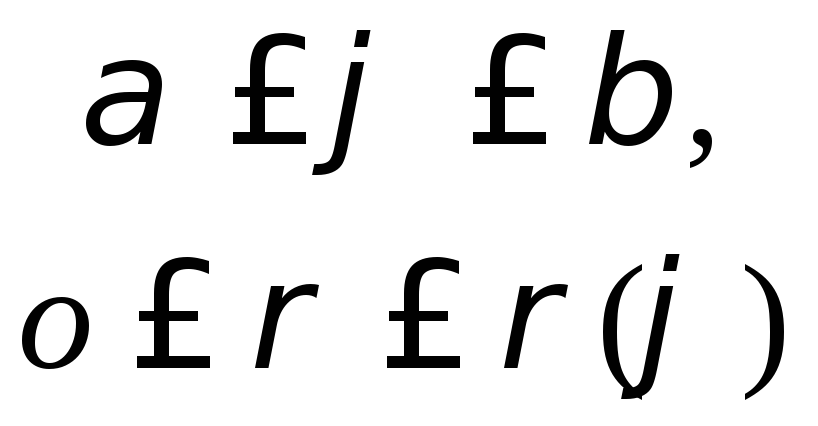
выразится интегралом

- площадь в полярных координатах

Элемент площади в полярных координатах есть главная частьприи равен площади кругового сектора:

26. Пример 26

Найти площадь фигуры, заключённой между параболой и прямой

Решение.

Найдём абсциссы точек пересечения линий, образующих фигуру:

_|

(кв.ед.)

Длина дуги кривой

Пусть - гладкая кривая (непрерывная вместе со своей производной).

Для нахождения длины дуги кривой используем метод дифференциала.

Из теоремы Пифагора для бесконечно малого треугольника:

- дифференциал дуги в прямоугольных координатах.

или .

Δy

Δl

y=f(x)

Δx

a

b

xa

x+Δx

Если кривая задана параметрически

непрерывно дифференцируемые функции

Тогда длина дуги находится по формуле

(Так как дифференциал дуги в этом случае .)

Если кривая задана уравнением в полярной системе координат, то длина дуги

(предполагая, чтоинепрерывны на сегменте.)

Эту кривую можно задать параметрически, принимая за параметр полярный угол .

Так как между полярными и декартовыми координатами существует зависимость , то, принимая во внимание, что, получим.

Таким образом, дифференциал дуги в полярных координатах:

Взяв интеграл по промежутку от до, получим длину дуги в полярных координатах

.

27. Пример 27

Найти длину кардиоиды .

0

l

2a

Решение.

Длина дуги в полярных координатах находится по формуле

Кардиоида симметрична относительно полярной оси. Изменяя полярный угол от 0 до, мы получим половину длины кардиоиды. Вся длина кардиоиды

(лин. ед.)

Лекция 5 Объём тела вращения

Если задана функция определяющая площадь поперечного сечения тела плоскостью, перпендикулярной осиОх, то объём этого тела вычисляется по формуле

- (лемма Архимеда)

Рассмотрим сначала объёмцилиндрического элемента как объём цилиндра, площадь основания которого, а высота

или

Интегрируя в пределах от до, получим объём всего тела

Объём тела, полученного вращением вокруг оси криволинейной трапецииAabB, где- длина кривой, вычисляется по формуле.

В этом случае сечение тела плоскостью есть круг с радиусом , площадь которогои.

Объём тела, полученного вращением вокруг осиОy криволинейной трапецииCcdD, гдеCD- кривая, вычисляется по формуле.

28. Пример 28

Найти объём тела, полученного вращением вокруг оси арки циклоиды,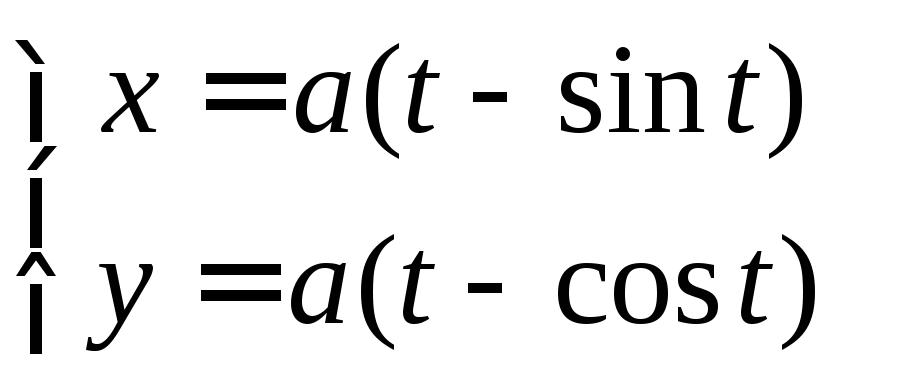

Решение.

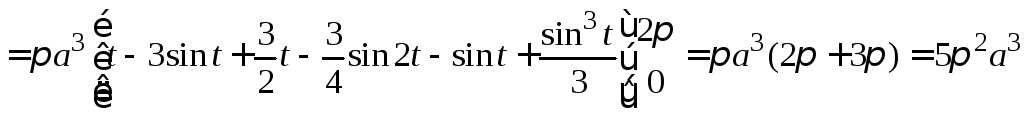(куб.ед.)