Понятие интегральной суммы и определённого интеграла.
Приведём схему построения интегральной суммы, которая применима для всех видов интегралов: определённого (на отрезке); двойного (в области на плоскости); тройного (в трёхмерной области); поверхностного (на поверхности); криволинейного (на кривой).
Пусть
непрерывна на отрезке
.
Разобьём
на
подсегментов произвольным образом
;
-
длина частичного сегмента.
Обозначим
- наибольшую из длин.
Выберемпроизвольную точку
;
Найдёмзначение функции
в точке
:
.
Составимпроизведение вида
;
Просуммируемих:
или с помощью знака
:
- интегральная сумма
на
Геометрически
представляет собой сумму площадей
прямоугольников с основанием
и высотой
.
Определение. Предел последовательности
интегральных сумм
при
(
),
не зависящий ни от способа деления
,
ни от выбора
,
называется определённым
интегралом
по промежутку
.
(5)
определённый
интеграл есть число, зависящее только
от подынтегральной функции
и пределов интегрирование
и
(нижней и верхней границы промежутка
интегрирования
) .
определённый
интеграл существует только для непрерывной
функции
на
и
называется
интегрируемой на этом отрезке.
Теорема существования определённого
интеграла (теоремаКоши): если
непрерывна
то она интегрируема
А также определённая и ограниченная
на
функция,
имеющая конечное число точек разрыва
на
интегрируема на этом промежутке; монотонная
на отрезке
функция интегрируема на
.
Геометрическиопределённый
интеграл от
на
численно равен площади криволинейной
трапеции с основанием
,
ограниченной кривой
и вертикалями
,
.
Пример 17
Найти
По определению из формулы (5), полагая
имеем
Таким образом, получим
Находить определённый интеграл с помощью интегральной суммы по определению, как вы убедились даже на простом примере, себе дороже. Тем более весома и значительна будет для нас формула Ньютона-Лейбница.
Лекция 3 Формула Ньютона-Лейбница.
Эта формула устанавливает связь между определённым и неопределённым интегралом.
Теорема.
Определённый интеграл равен приращению первообразной на промежутке интегрирования.
- формула Ньютона- Лейбница.
Доказательство.
Пусть
{
по теореме Лагранжа о конечных приращениях,
т.к. 
ч.т.д.
Пример 18
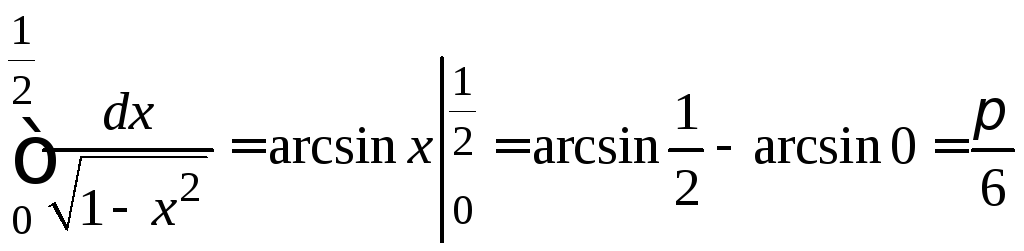
Основные свойства определённого интеграла.
Определённый интеграл не зависит от переменной интегрирования.
Интеграл с одинаковыми пределами интегрирования равен нулю.
При перемене пределов интегрирования знак интеграла меняется на противоположный.
Доказательства следуют из формулы Ньютона-Лейбница.
линейность определённого интеграла.
Теорема о среднем.
Определённый интеграл от непрерывной функции равен произведению длины промежутка интегрирования на значение функции в некоторой промежуточной точке.
Доказательство.
{по
теореме Лагранжа}
ч.т.д.
Если
знакопостоянна на
,
то
имеет тот же знак, что и функция.
Доказательство.
По теореме о среднем:
ч.т.д.
Если
.
Доказательство.
ч.т.д.
Если
и
-
наименьшее и наибольшее значение функции
на
,
то
Доказательство.
По условию
Возьмём интегралы от всех частей двойного
неравенства.используя
свойство 7 и пример 17, получим
ч.т.д.
Следствие.
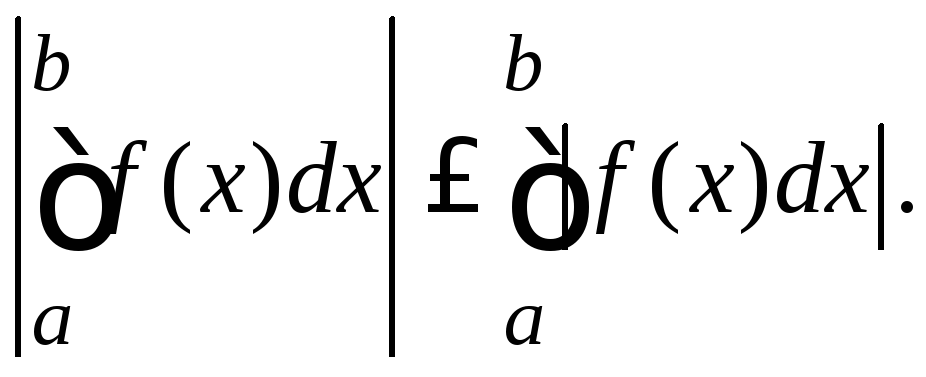
Так как
Теорема о разбиении промежутка интегрирования (свойство аддитивности).
Для любых трёх чисел
справедливо равенство
т.е. интеграл по всему отрезку равен сумме интегралов по его частям.
Доказательство.
ч.т.д.
Пример 19
.