Интегрирование иррациональных функций.

Интеграл от любой рациональной функции всегда может быть найден. И он выражается через рациональные функции, логарифм и арктангенсы, т.е. является элементарной функцией. Это замечание существенно, т.к. во многих случаях интегралы даже от очень простых функций уже не будут функциями элементарными и их невозможно привести к табличным интегралам. Поэтому очень часто при интегри­рова­нии необходимо отыскать такую замену переменной, которая приводила бы данный интеграл к интегралу от рациональной функции. О таких заменах говорят, что они рационализируют интеграл.

Рассмотрим ,

где - выражение, рациональное относительно своих аргументов (т.е. в этом выражении над величинами производятся только рациональные действия).

Пусть - общий знаменатель дробей. Данный интеграл приводится к интегралу от рациональной функции подстановкой

12. Пример 12

.

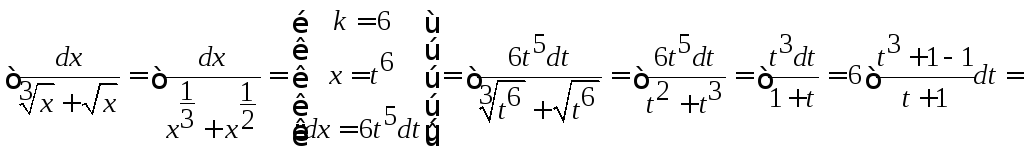
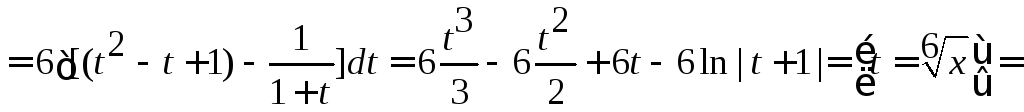
Этот интеграл сводится к интегралу от рациональной функции с помощью подстановки , где- общий знаменатель дробей.

13. Пример 13

Интегрирование тригонометрических выражений.

Рассмотрим . где - выражение, рациональное относительно своих аргументов.

преобразуем в интеграл от рациональной функции с помощью подстановки- универсальная тригонометрическая подстановка:

14. Пример 14

Наряду с универсальной тригонометрической подстановкой необходимо знать также и другие подстановки, которые быстрее приводят к цели. Так, например, если ивходят в выражение функции R только в чётных степенях, то гораздо удобнее применить подстановку.

Рассмотрим интеграл вида , гдеи- целые числа.

Если - нечётное положительное число, то применяют подстановку,:

Если - нечётное положительное число, то аналогично применяют подстановку,.

15. Пример 15

Если и- чётные положительные числа.

16. Пример 16

положим,.

,.

Возводя в степень и раскрывая скобки, получим члены, содержащие в чётных и нечётных степенях.

Если оба показателя – чётные, причём хотя бы один из них отрицателен, то применяют подстановку ;

Если оба показателя и– отрицательные и сумма их чётная, то подстановкаснова приводит интеграл к сумме интегралов от степенных функций.

Для интегралов вида

применяем формулы:

Тогда, например, будем иметь

.

Лекция 2 Определённый интеграл, как предел интегральных сумм.

Понятие возникает в работах Ферма, Декарта, Паскаля, затем Ньютона, Лейбница. Сам термин принадлежит Лапласу. Современное обозначение определённого интеграла появляется в знаменитой "Аналитической теории тепла" Фурье (1822г.).

Задачи, приводящие к понятию определённого интеграла.

Задача о площади криволинейной трапеции.

Найдём площадь криволинейной трапеции – фигуры, ограниченной дугойграфика непрерывной функциис основаниеми, в общем случае, прямыми

Алгоритм действий (с ключевыми словами).

Разобьёмотрезокточкаминачастичных отрезков,Обозначим

Выберемпроизвольную точкуи найдём

Составимпроизведение видаравное площади прямоугольника с высотойи основанием

просуммируемэти произведения:

-

есть площадь ступенчатой фигуры равной приближённо S – значению площади криволинейной трапеции. Тем более точно, чем больше число разбиений и чем меньше длины частичных сегментов.

Переходимк пределу:(1)

Задача о работе переменной силы.

Найдём работу А переменной силы (значения которой есть функция), действующей вдоль пути

Разобьёмнаучастков,ОбозначимСилу на достаточно малом отрезкеможно приближённо считать постоянной и равной значению функции, в произвольной точке

Выберемпроизвольную точкуи найдём

Составимпроизведение видаработе на участке(как работа постоянной силы).

Просуммируем:– приближённое значение работы силына всём пути.

Переходимк пределу:(2)

Задача о пройденном пути.

Пусть закон изменения мгновенной скорости есть функция времени . Требуется найти путь, пройденный за отрезок времени

Разобьёмотрезок времени начастичных промежутков Если эти промежутки времени достаточно малы, то движение на каждом участке можно считать равномерным.

Выберемпроизвольно

Составимпроизведение видапути за время.

Просуммируем:– приближённое значение путиза время отдо T тем точнее, чем меньше каждый из временных промежутков.

Переходимк пределу:(3)

Задача о количестве вещества, вступившего в реакцию.

Пусть скорость химического превращения некоторого вещества есть функция времени . Найти количествовступившего в реакцию вещества за промежуток времени отдо T.

Проделав последовательно те же операции (наш алгоритм с ключевыми словами), получим

(4)

(самостоятельно).

И, хотя все решённые нами задачи имеют различный смысл, математический аппарат для их решения один и тот же. Во всех этих задачах получаем выражения одного и того же вида (1) – (4).