Лекция12

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.

Рассмотрим линейное неоднородное дифференциальное уравнение 2-го порядка спостоянными коэффициентами и с правой частью в виде функцииопределённого вида

Из теоремы о структуре общего решения линейного неоднородного ДУ следует, что для решения неоднородного уравнения необходимо найти какое-нибудь его частное решение и общее решение соответствующего ему однородного уравнения. Сумма этих функций и даёт общее решение неоднородного уравнения .

Мы подробно рассмотрели, как находится общее решение однородного уравнения.

Подбор частного решения неоднородного уравнения в зависимости от вида функции в тех случаях, когда она представляет собой произведение многочлена на показательную функцию, многочлен или тригонометрическую функцию, показан в таблице.

Частные решения линейного неоднородного ДУ 2-го порядка в зависимости от вида функции .

	Вид функции	Корни характеристического уравнения	Вид частного решения
	-известный многочлен n-ой степени	1) 2) 3)
		1) 2)	-многочлен той же степени, что ис неизвестными коэффициентами (в общем виде)
	- известные многочлены	1) 2)	и- неизвестные многочлены степени, равной высшей из степеней многочленов
	A,B,b-заданные числа	1) 2)	L,M-неизвестные постоянные

Неизвестные коэффициенты находятся методом неопределённых коэффициентов, который разберём на примерах.

40. Пример 51

Найти частное решение уравнения

удовлетворяющее начальным условиям

Характеристическое уравнение

имеет корни . Поэтому однородное уравнение имеет общее решение

Общее решение неоднородного уравнения

Ищем частное решение неоднородного уравнения:

т.к. -многочлен 1-ой степени.

Тогда .

По таблице (случай 1.2) будем искать частное решение в виде

Находим производные

Подставляем ив неоднородное уравнение и, сокращая на, получаем тождество

_{(исправить)}

После приведения подобных членов получим

Приравниваем коэффициенты при одинаковых степенях

Таким образом,

и общее решение ДУ:

Найдём ииз начальных условий.

Продифференцируем общее решение:

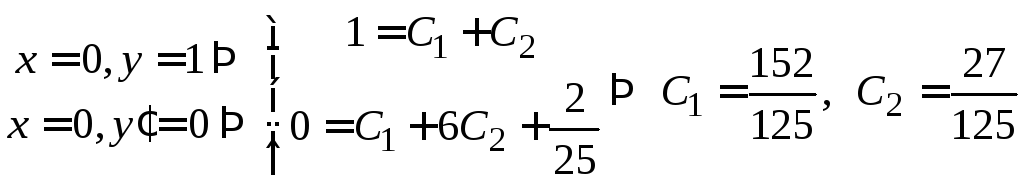
Подставляя ив общее решение неоднородного уравнения, получим его частное решение, удовлетворяющее начальным данным

.

40. Пример 52

Найти общее решение уравнения

Найдём общее решение однородного уравнения

Правая часть - многочлены нулевой степени,(случай 4.2 ).

Дифференцируем дважды

и, подставляя ив заданное уравнение, получим

_{После приведения подобных членов получим}

Приравниваем коэффициенты при и:

Таким образом, и общее решение неоднородного уравнения запишется в виде

.