Лекция11

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Пусть в уравнении

(1)

коэффициенты и- какие-либо числа (константы).

Используя подстановку Эйлера, будем искать частные решения уравнения в виде

(2)

где подлежащая определению.

Подставим в уравнение (1)

Получим

(3)

Алгебраическое уравнение (3) для определения называетсяхарактеристическим уравнением линейного ДУ (1). В зависимости от корней

находим общее решение линейного однородного ДУ.

1. Пусть - корни характеристического уравнения, действительные и различные. Тогда полученные частные решения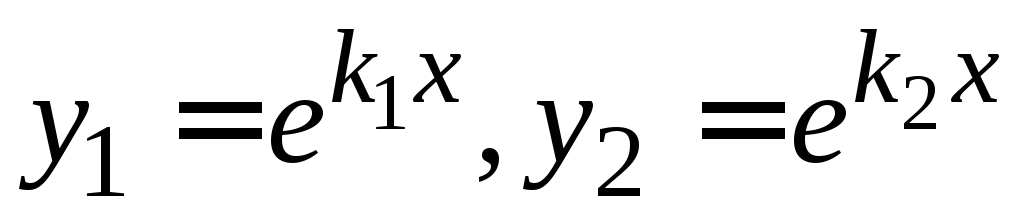образуют фундаментальную систему решений (пример 46.1). Следовательно, общее решение (по теореме о структуре общего решения линейного однородного уравнения) имеет вид(4)

2. Пусть - корни характеристического уравнения, действительные и равные. Тогдат.е.ине являются фундаментальной системой решений линейного однородного ДУ. Линейно независимой по отношению к функции является, в частности, функция

Докажем, что она удовлетворяет уравнению (1):

. Нотак какесть корень характеристического уравнения (3).

Кроме того, по теореме Виета

Поэтому Следовательно,т.е. функциядействительно является решением уравнения (1).

Таким образом, в рассматриваемом случае общее решение однородного уравнения

имеет вид:

или(5)

3. корни характеристического уравнения - комплексно-сопряжённые числа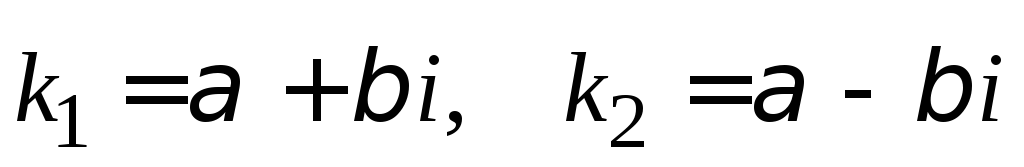. Фундаментальная система решений однородного уравнения в этом случае будет

.

Тогда общее решение имеет вид

(6)

Полученные результаты в обобщённом виде представлены в таблице.

Общее решение линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами.

	Корни характеристического уравнения	Фундаментальная система решений	Общее решение уравнения

40. Пример 47

Найти общее решение уравнения

.

Составим характеристическое уравнение.k² – 3k+ 2 = 0,k₁ = 1,k₂ =2.

Корни различные. Фундаментальная система решений имеет вид:

Тогда по формуле общее решение уравнения будет

.

40. Пример 48

Найти общее решение уравнения .

Составим характеристическое уравнение фундаментальная система решений и по формуле

-общее решение.

40. Пример 49

Найти общее решение уравнения .

Составим характеристическое уравнение

Фундаментальная система решений имеет вид:

и по формуле общим решением уравнения будет

.

Линейные однородные дифферинциальные уравненияn-го порядка с постоянными коэффициентами

(1)

Теорема о структуре общего решения линейного однородного уравнения.

Если функции является линейно независимыми решениями (фундаментальная система решений) уравнения (1), то его общее решение есть

(2)

где - произвольные постоянные.

Составим характеристическое уравнение

Находим корни характеристического уравнения. По характеру корней выписываем частные линейно независимые решения:

1. каждому действительному однократному корню соответствует частное решение;

2. каждой паре комплексно сопряжённых однократных корней 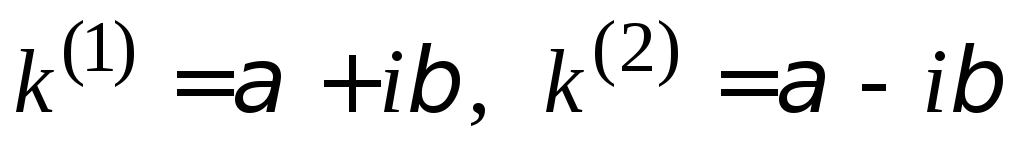соответствуют два частных решения:;

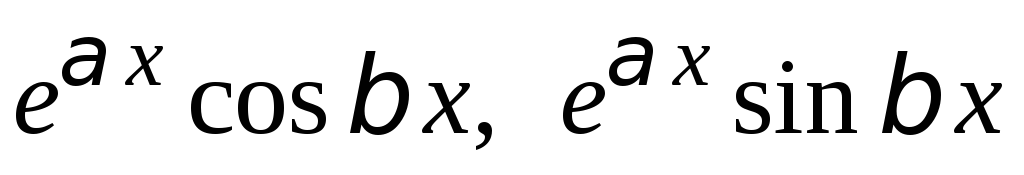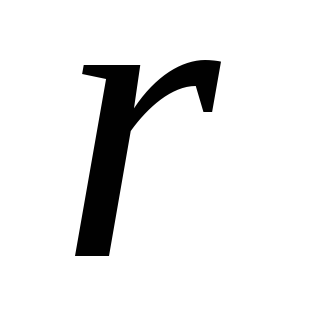3. каждому действительному корню кратностисоответствуетлинейно независимых решений;

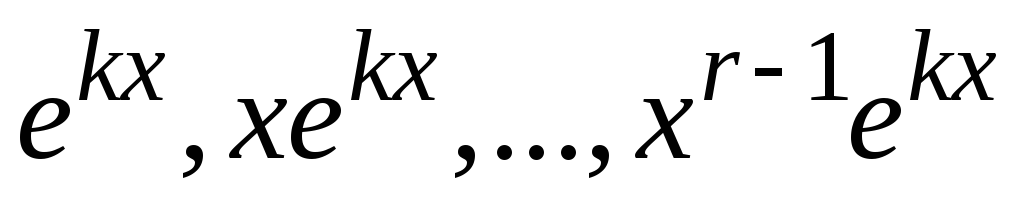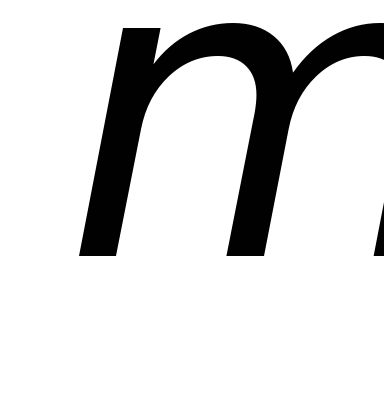4. каждой паре комплексно сопряжённых корней кратностисоответствуютчастных решений

40. Пример 50

Решить линейное однородное ДУ 3-го порядка

.

Составим характеристическое уравнение

- фундаментальная система решений.

Общее решение

- общее решение нашего ДУ 3-го порядка.

Сделать проверку!