Лекция 9 Понятие о дифференциальных уравнениях высших порядков. Задача Коши.

Дифференциальное уравнение -го порядка имеет вид

(1)

или

Общее решение содержит произвольных постоянных

Задача Коши.

Найти частное решение уравнения (1), удовлетворяющее начальным условиям

Дифференциальные уравнения второго порядка.

Уравнение 2-го порядка в общем виде может быть записано

или

Общее решение (общий интеграл) ДУ 2-го порядка

или

Задача Коши.

Найти частное решение удовлетворяющее уравнениюи заданным начальным условиям.

Теорема Коши(теорема существования и единственности).

Пусть правая часть уравненияи её частные производныеиопределены и непрерывны в некоторой области изменения переменныхи.тогда для любой точки этой области, данное уравнение имеет единственное решениеудовлетворяющее начальным условиям

Уравнения, допускающие понижение порядка.

Рассмотрим 3 типа уравнений, допускающих понижение порядка.

	Тип уравнения	Общий вид уравнения	Метод решения уравнения
	уравнение явно не содержити		Порядок понижается путём последовательного интегрирования - - общее решение
	уравнение явно не содержит функции		Подстановка: -общее решение
	уравнение явно не содержит независимой переменной		Подстановка: Подставляя в уравнение иполучим ДУ 1-го порядка относительно. - общий интеграл

40. Пример 45

Найти общее решение дифференциального уравнения второго порядка

.

Решение.

Уравнение явно не содержит . Сделаем подстановку.

Подставляя в уравнение получим:- уравнение с разделяющимися переменными относительнои:

так кактоили

- общий интеграл нашего дифференциального уравнения.

Лекция10

Линейные дифференциальные уравнения второго порядка.

Определение.

Уравнение вида (1)

называется линейным неоднородным дифференциальным уравнением 2-го порядка.

Если , то уравнение называется однородным:

. (2)

и- заданные функции отили константы – коэффициенты уравнения.

Общее решение однородного уравнения складывается из линейно независимых частных решений.

Функции иназываются линейно независимыми на интервале, если равенство

(*)

где , выполняется тогда и только тогда, когда.

Если хотя бы одно из чисел илиотлично от нуля и выполняется равенство (*), то функциииназываются линейно зависимыми на интервале.

Очевидно, что функции илинейно зависимы тогда и только тогда, когда они пропорциональны, т.е. для всехвыполняется равенство, или,.

Cпомощью определителя Вронского - вронскиана (Ю.Вронский – польский математик) также устанавливается линейная независимость системы функций.

Для двух дифференцируемых функций ивронскиан имеет вид

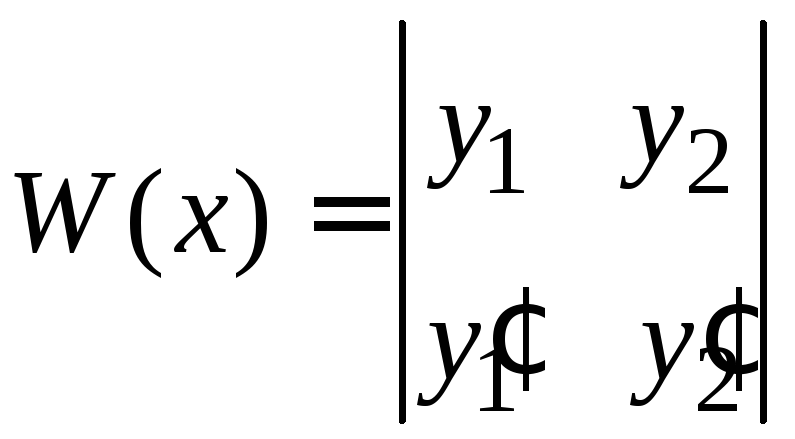
Теорема.

Если дифференцируемые функции илинейно зависимы на, то определитель Вронского на этом интервале тождественно равен нулю.

Так как функции илинейно зависимы, то в равенстве (*) значениеилиотлично от нуля. Пусть, тогда. Поэтому для любого

для линейно независимых функций вронскиан отличен от нуля.

40. Пример 46

Исследовать на линейную зависимость функции:

1) и.

Так как то функции линейно независимы.

или составим вронскиан:

функции линейно независимы.

2) и- линейно зависимые функции, т.к. они пропорциональны..

Для них вронскиан .

Определение.

Два линейно независимых частных решения линейного однородного уравнения образуют фундаментальную систему решений.

Теорема. (О структуре общего решения линейного однородного уравнения).

Если иесть фундаментальная система решений линейного однородного уравнения, то его общее решениеравно

, (3)

гдеи- произвольные постоянные.

Доказательство.Подставимив уравнение (2).

_.

(Так как и- частные решения, удовлетворяющие уравнению (2) по условию теоремы).

Остаётся доказать, что это решение общее, т.е. что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям

где .

Подставив начальные условия в решение (3) получим систему уравнений

где , с неизвестнымии.

Определитель этой системы

равен значению вронскиана при.

Так как решения иобразуют фундаментальную систему решений наито,. Поэтому система уравнений имеет единственное решение

.

Решение является частным решением уравнения (2), удовлетворяющим начальным условиям. Ч.т.д.

Теорема. (О структуре общего решения линейного неоднородного ДУ).

Общее решение неоднородного уравнения является суммойобщего решения , соответствующего ему однородного уравнения и частного решениянеоднородного уравнения.

Доказательство. Покажем, что решениеудовлетворяет уравнению

т.е. получено тождество

так какудовлетворяет однородному уравнению иесть частное решение неоднородного уравнения ( по условию теоремы)

Линейные однородные дифференциальные уравнения n-го порядка

Обобщим полученные результаты для линейных однородных дифференциальных уравнений -го порядка:

(4)

Функции называютсялинейно независимыминаесли равенствовыполняется лишь в случае, когда все числа. В противном случае (если хотя бы одно из чиселне равно нулю) функции-линейно зависимы.

Определитель Вронского

для линейно независимых функций отличен от нуля и равен нулю для линейно зависимых функций.

линейно независимые частные решениялинейного однородного уравнения (4) образуютфундаментальную систему решений.

Общее решение линейного однородного ДУ -го порядка имеет вид

,

где - произвольные постоянные,- частные решения, образующие фундаментальную систему.