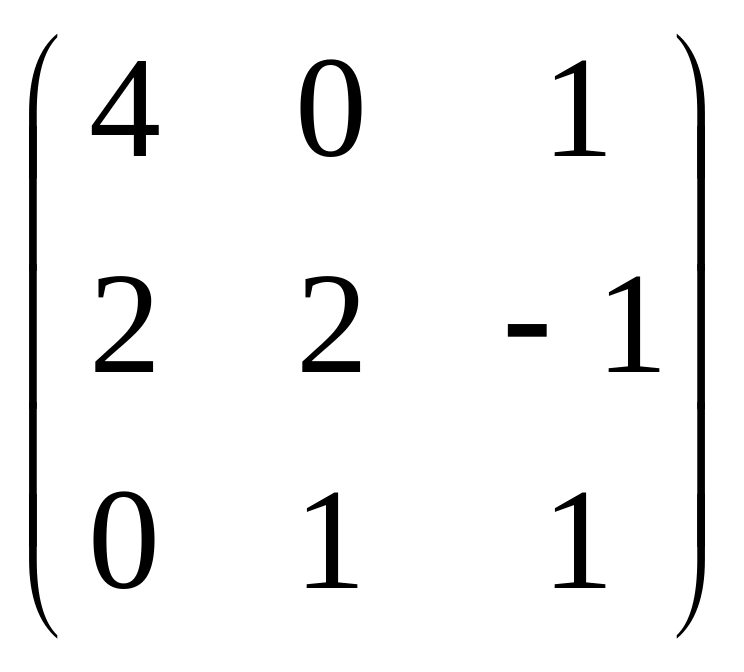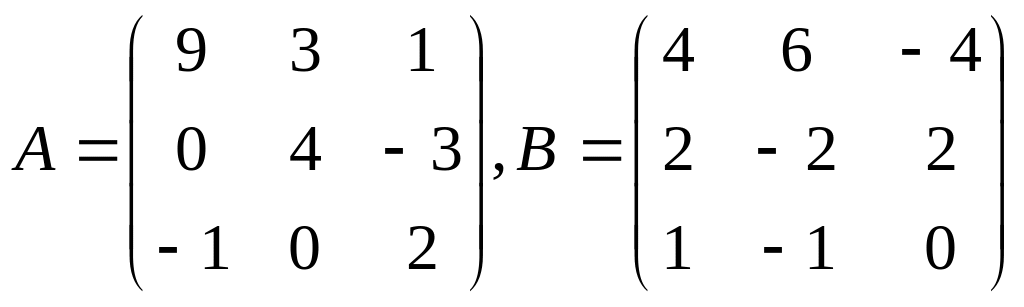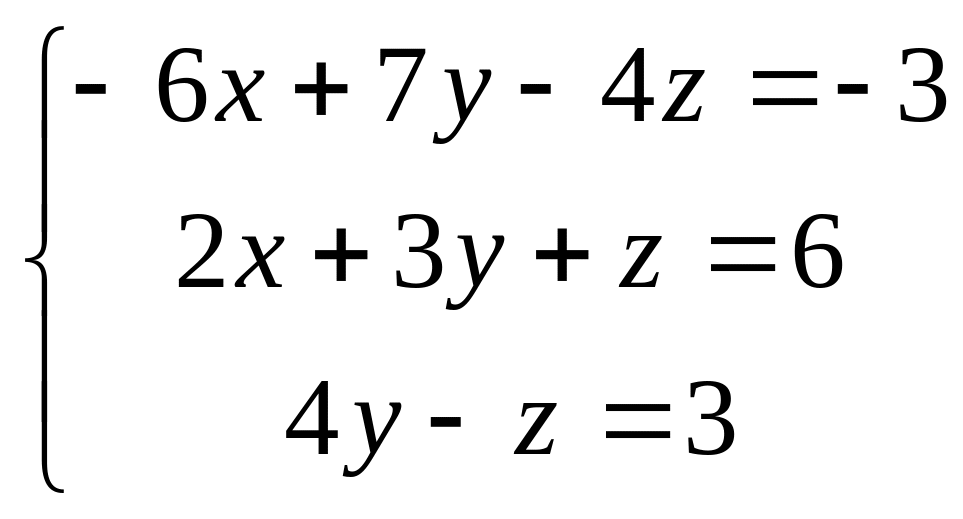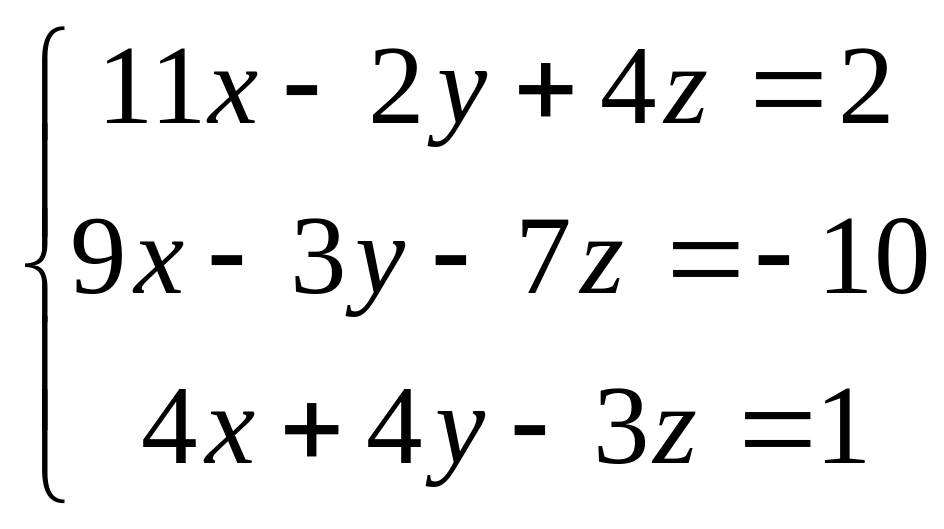Вопросы
по дисциплине
Вопросы
по дисциплине
«Математика»
Понятие вектора.
Умножение и сложение векторов.
Матрицы: определитель, обратная матрица, транспонированная матрица, сложение, умножение матриц.
Решение системы алгебраических уравнений методом Крамера.
Решение системы алгебраических уравнений методом обратной матрицы.
Общее уравнение прямой.
Уравнение прямой в отрезках.
Уравнение прямой с угловым коэффициентом.
Уравнение прямой проходящей через две заданные точки.
Расстояние от точки до прямой.
Общее уравнение плоскости.
Основные виды задач на прямую и плоскость.
Линии второго порядка: окружность её уравнения и основные характеристики.
Линии второго порядка: эллипс его уравнение и основные характеристики.
Линии второго порядка: гипербола её уравнение и основные характеристики.
Линии второго порядка: парабола её уравнения и основные характеристики.
Механический смысл производной
Геометрический смысл производной
Производная обратной функции
Производная сложной функции
Дифференциал
Исследование функций и построение их графиков
Исследование функции на монотонность и экстремумы
Необходимое условие экстремума
Критические точки: определение и способы нахождения
Контрольная работа п о дисциплине «Математика»
ЗАДАНИЕ №1
Вычислить определитель каждой квадратной матрицы:
а)
 б)
б)
 в)
в)
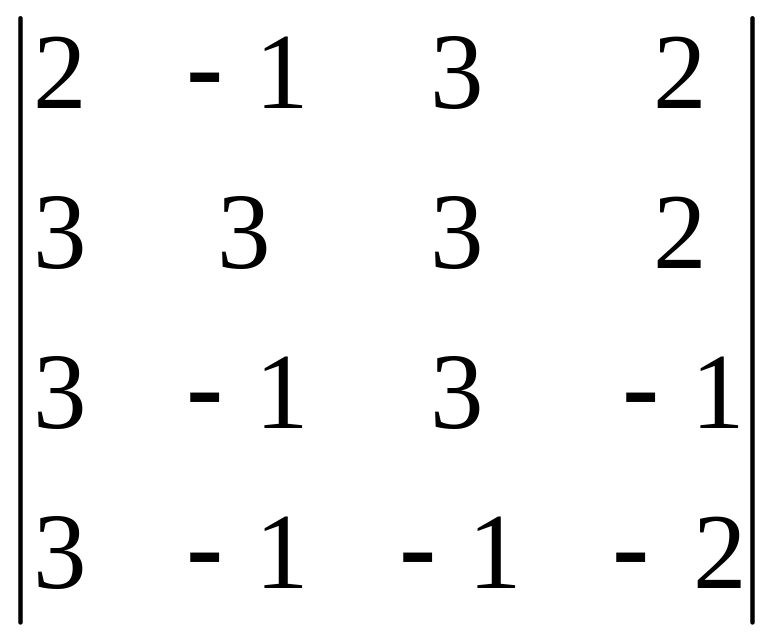
а)
 ,
б)
,
б)
 ,
в)
,
в)

а)
 б)
б)
 в)
в)

а)
 б)
б)
 в)
в)

а)
 б)
б)
 в)
в)

а)
 ,
б)
,
б)
 ,
в)
,
в)

а)
 ,
б)
,
б)
 ,
в)
,
в)

а)
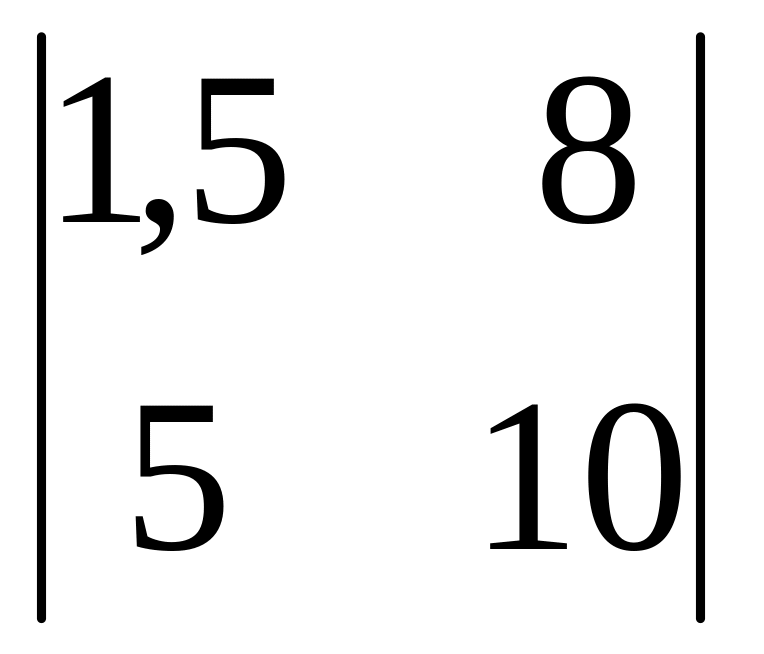 ,
б)
,
б)
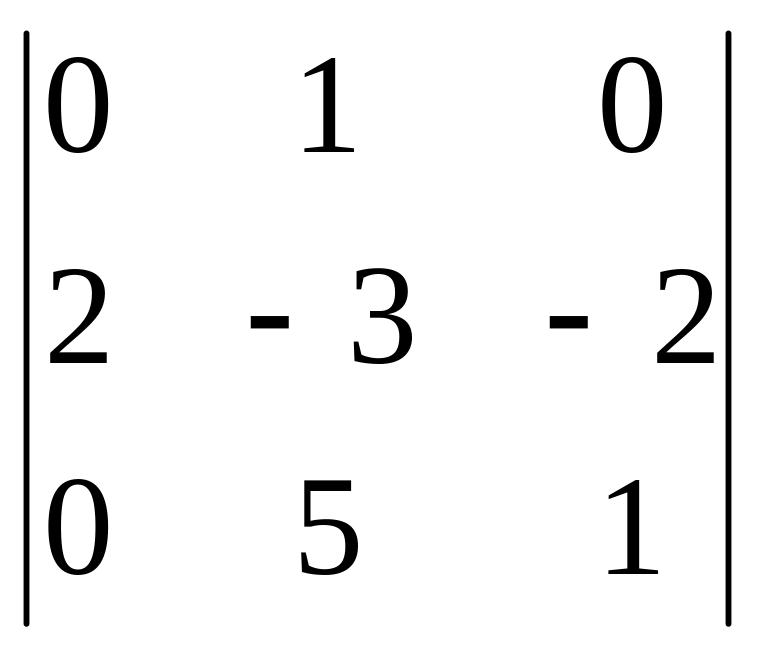 ,
в)
,
в)

а)
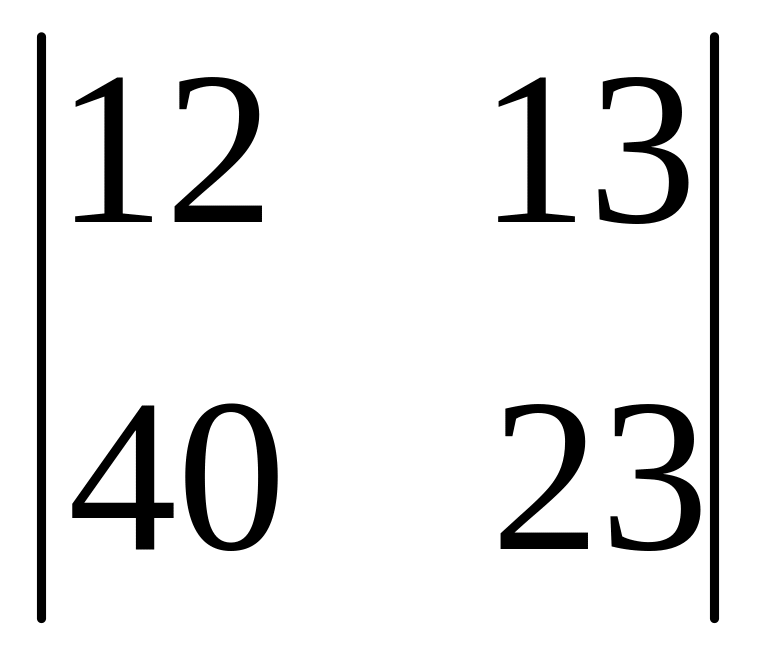 ,
б)
,
б)
 ,
в)
,
в)

а)
 ,
б)
,
б)
 ,
в)
,
в)

ЗАДАНИЕ №2
Для данной матрицы вычислить обратную матрицу:
ЗАДАНИЕ №3
Даны матрицы А и В. Вычислить:
а) 2А+3В;
б) АВ-ВА.
ЗАДАНИЕ №4
Задать векторы
![]() произвольной
длины и направления (задание одинаково
для всех вариантов).
произвольной
длины и направления (задание одинаково
для всех вариантов).
Построить:
а)
![]()
б)![]()
в)![]()
ЗАДАНИЕ №5
Найдите скалярное
и векторное произведение векторов
![]() и
и
![]() :
:
а)

б)![]()
а)

б)![]()
а)

б)![]()
а)

б)![]()
а)

б)![]()
а)
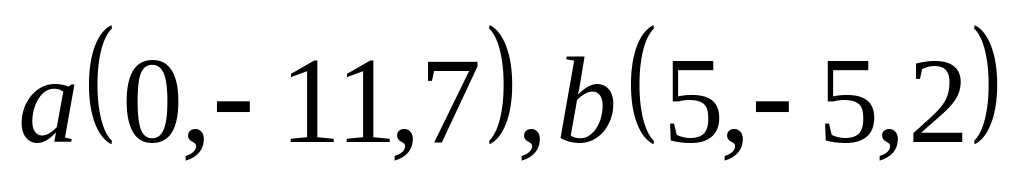
б)![]()
а)

б)![]()
а)

б)![]()
а)

б)![]()
а)

б)![]()
ЗАДАНИЕ №6
Найти скалярное произведение векторов (ab) и (ac), если:
 ,
,
 .
.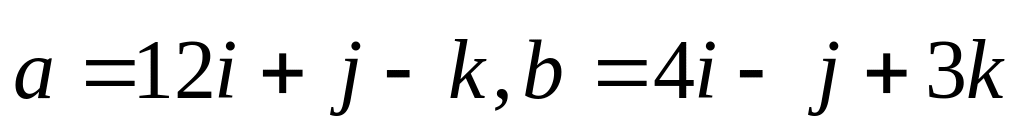 ,
,
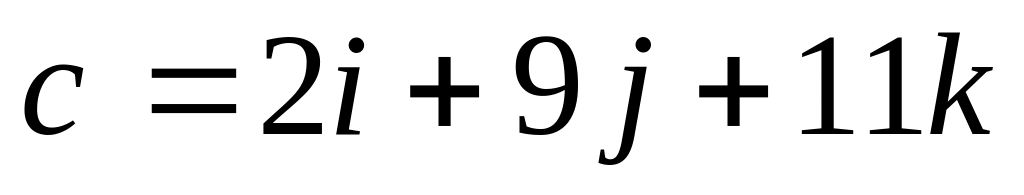 .
. ,
,
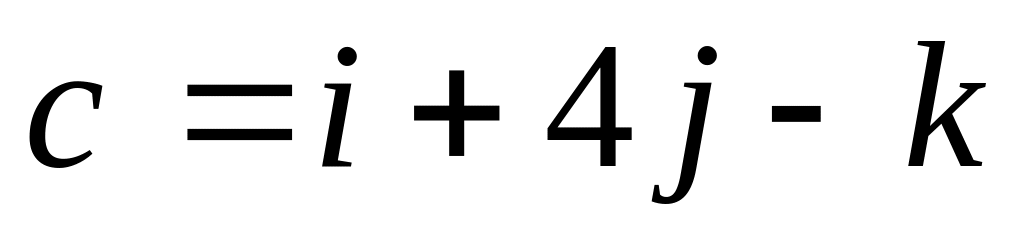 .
. ,
,
 .
. ,
,
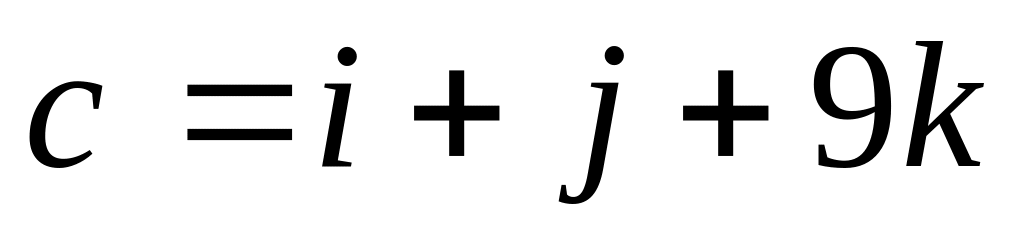 .
. ,
,
 .
. ,
,
 .
. ,
,
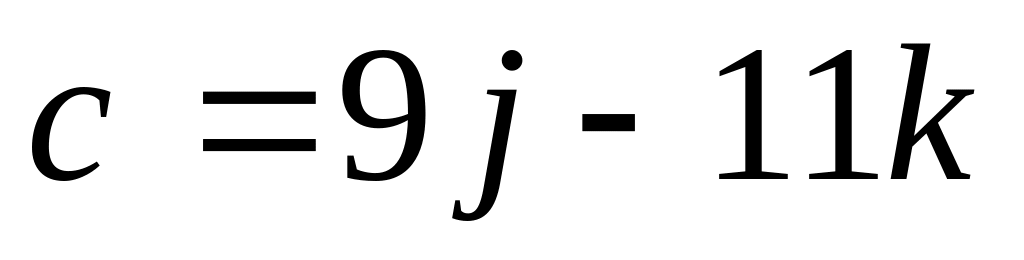 .
. ,
,
 .
. ,
,
 .
.
ЗАДАНИЕ №7
Решить систему алгебраических уравнений:
а) методом Крамера,
б) методом обратной матрицы,
в) методом Гаусса.
ЗАДАНИЕ №8
Линии первого порядка
Найти точку пересечения двух прямых:
![]()
Найти угол, образованный прямыми:
![]()
Составить уравнение прямой, проходящей через точки:
![]()
Найти расстояние от точки М(-1,1) до прямой 4x-3y+6=0.
Составить уравнение прямой и построить прямую на чертеже, если ее угловой коэффициент равен (-1/3) и прямая отсекает отрезок на оси Оу равный 2/3.
Составить уравнение прямой проходящей через начало координат, перпендикулярно прямой y=-x+4.
Составить уравнение прямой проходящей через начало координат, параллельно прямой y=-x+4.
Составить уравнение прямой, проходящей через точки:
![]()
Составить уравнение прямой проходящей через точку Р(3,-6), параллельно прямой y=-x+4.
Составить уравнение прямой, проходящей через точку Р(3,-6), перпендикулярно прямой y=-x+4.
ЗАДАНИЕ №9
Линии второго порядка
Фокусное расстояние эллипса равно 8 см, малая ось равна 6см. Найти большую ось и эксцентриситет.
Фокусное расстояние гиперболы равно 10 см, мнимая ось равна 6см. Найти действительную ось, эксцентриситет и асимптоты.
Найти координаты центра и радиус окружности
![]()
Написать каноническое уравнение параболы с фокусным расстоянием, равным 3.
Составить уравнение окружности, если ее центр совпадает с началом координат и прямая 3x-4y+20=0 является касательной к окружности.
Установить, как расположена точка А (1,-2) относительно окружности
 .
.Составить уравнение эллипса, если известны его эксцентриситет е=1/2, фокус F(3,0) и уравнение соответствующей директрисы x+y-1=0.
Определить полуоси каждого из следующих эллипсов:
а)
![]()
б)
![]() ;
;
в)
![]()
Определить полуоси каждой из следующих гипербол:
а)
![]()
б)
![]()
в)
![]()
Определить точки гиперболы
 ,
расстояния от которых до правого фокуса
равно 4,5.
,
расстояния от которых до правого фокуса
равно 4,5.
Требования к написанию