2. Построение таблицы покрытий

Таблица 5

Таблица покрытий

3. Нахождение существенных импликант (ядра покрытия)

Из таблицы 5 видно, что для искомой функции простая импликанта «-10-» является существенной импликантой и образует ядро покрытия функции. Удаляем из таблицы 5 строку, соответствующую найденной существенной импликанте, и столбцы, которые ею покрываются (табл. 6).

Таблица 6

Таблица покрытий

4. Выбор минимального покрытия максимальными интервалами. Для рассматриваемой функции выбираем покрытие из простых импликант «0-11» и «10-1», так как они покрывают в таблице 2 все оставшиеся после пункта 3 столбцы.

Минимальная ДНФ для заданной функции имеет вид:

.

1.7. Метод Квайна–Мак-Класки для минимизации не полностью определенных функций

Для минимизации не полностью определенных функций строятся две вспомогательные функции: функция нулевого доопределения и функция единичного доопределения . Функция нулевого доопределения получается заменой неопределенностей на «0», а функция единичного доопределения – заменой неопределенностей на «1». После этого задача сводится к нахождению минимального покрытия конституент единицы функции нулевого доопределения простыми импликантами функции единичного доопределения.

Пусть задана функция:

.

В начале определяются функции нулевого и единичного доопределения данной функции:

1. Функция нулевого доопределения равна тем наборам, на которых функция принимает истинные значения:

;

Функция единичного доопределения равна тем наборам, на которых функция принимает истинные значения и наборам, на которых функция не определена ( ):

.

2. Определим простые импликанты функции. Для этого разобьем на непересекающиеся подгруппы, в соответствии с количеством единиц в номере, функцию единичного доопределения и произведем операцию склеивания между этими группами:

Простые импликанты выделены овалом. Зачеркнуты одинаковые минитермы.

Строим таблицу покрытий, причем она по структуре совпадает с таблицей покрытий из метода Квайна–Мак-Класки для полностью определенных случаев, за исключением того, что в столбцах таблицы покрытий располагают минитермы ранга n, входящие в функцию нулевого доопределения.

Таблица 7

Таблица покрытий

Из таблицы 7 видно, что для искомой функции простые импликанты «-01-» и «-100» являются существенными импликантами и образуют ядро покрытия функции. Удаляем из таблицы 3 строки, соответствующие найденным существенным импликантам, и столбцы, которые ими покрываются (табл. 8).

Таблица 8

Таблица покрытий

Для рассматриваемой функции выбираем покрытие из одной простой импликанты «--11», покрывающей в таблице 8 оставшийся столбец.

Минимальная ДНФ для заданной функции имеет вид:

.

1.8. Разложение Шеннона по k переменным

Любая функция представима в виде разложения Шеннона:

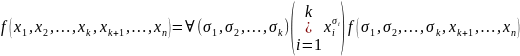
где,

Дана функция: .

Разложение Шеннона для заданной функции осуществим по переменным :

.

В соответствии с вышепредставленным выражением осуществим подстановку указанных значений переменных в заданную функцию. Получаем следующее разложение Шеннона для функции :

.

Предельное разложение Шеннона (k = n) функции , не равной 0, имеет вид:

(9)

Предельное разложение Шеннона функции алгебры логики является ее совершенной дизъюнктивной нормальной формой (предельное разложение осуществляется по всем переменным одновременно).

Дана функция: .

Предельное разложение Шеннона для представленной функции выглядит следующим образом:

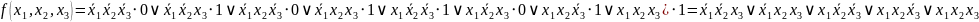. (10)