
- •Хасцаев б. Д.
- •Содержание
- •Введение
- •1. Основные теоретические положения
- •1.1. Основные положения алгебры логики
- •1.2. Основные тождества (законы и правила) алгебры логики
- •1.3. Нормальные формы функций алгебры логики
- •1.4. Минимизация функций алгебры логики в классе днф
- •Соответствие десятичных эквивалентов двоичным наборам
- •1.5. Метод неопределенных коэффициентов
- •1.6. Метод Квайна–Мак-Класки для минимизации полностью определенных функций
- •2. Построение таблицы покрытий
- •3. Нахождение существенных импликант (ядра покрытия)
- •1.7. Метод Квайна–Мак-Класки для минимизации не полностью определенных функций
- •1. Функция нулевого доопределения равна тем наборам, на которых функция принимает истинные значения:
- •Функция единичного доопределения равна тем наборам, на которых функция принимает истинные значения и наборам, на которых функция не определена ( ):
- •1.8. Разложение Шеннона по k переменным
- •1.9. Дифференцирование функций алгебры логики
- •1.10. Метод каскадов
- •Определение веса производной
- •Определение веса производной
- •Определение веса производной
- •Определение веса производной
- •Определение веса производной
- •2. Структура курсового проекта
- •Литература
- •3. Синтез логической схемы
- •Образец оформления списка литературы
- •4. Литература
1.2. Основные тождества (законы и правила) алгебры логики
1) Закон коммутативности для дизъюнкции и конъюнкции:
 ;
;
 =
= .
.
2) Закон ассоциативности для дизъюнкции и конъюнкции:


3) Первый и второй законы дистрибутивности:


4) Законы идемпотентности для дизъюнкции и конъюнкции:
 ;
;
 .
.
5) Правила операций с константами:
 ;
;

 ;
;

6) Правила де Моргана:


7) Законы инверсии для дизъюнкции и конъюнкции:


8) Первый и второй законы склеивания:


9) Первый и второй законы поглощения:


10) Правило двойной инверсии:

1.3. Нормальные формы функций алгебры логики
Элементарной
конъюнкцией
называется конъюнкция, в которую каждая
переменная входит только один раз либо
с отрицанием, либо без него ( ). Число переменных конъюнкции называется
рангом
элементарной конъюнкции.
). Число переменных конъюнкции называется
рангом
элементарной конъюнкции.
Дизъюнктивной
нормальной формой (ДНФ)
называется дизъюнкция элементарных
конъюнкций ( ;
;
 и т. д.). Число элементарных конъюнкций,
образующих ДНФ, называется ее длиной.
и т. д.). Число элементарных конъюнкций,
образующих ДНФ, называется ее длиной.
Конституентой
называется
элементарная конъюнкция ранга n,
включающая все переменные функции
алгебры логики
 .
Общее число таких конституент равно
2n,
т. е. числу наборов n-переменных.
.
Общее число таких конституент равно
2n,
т. е. числу наборов n-переменных.
Конституентой единицы называется конституента, на которой функция алгебры логики обращается в единицу.
Любая функция алгебры логики, кроме нуля, может быть представлена в следующей форме:

где,
 ;
;
 – степень переменной
– степень переменной
 (если она равна 1, то переменная
записывается без отрицания (
(если она равна 1, то переменная
записывается без отрицания ( ),
а если равна 0, то переменная
записывается в инверсной форме (
),
а если равна 0, то переменная
записывается в инверсной форме (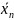 ).
).
При этом дизъюнкция в правой части (1) берется по тем наборам переменных, на которых функция, заданная таблицей истинности, обращается в единицу, т. е. берутся только конституенты единицы.
Представление функции алгебры логики в виде (1) называется дизъюнктивной совершенной нормальной формой (ДСНФ).
В итоге ДСНФ это ДНФ, все конъюнкции которой имеют один и тот же ранг, равный числу переменных функции.
Любая функция алгебры логики имеет единственную ДСНФ. Для получения ДСНФ функции алгебры логики удобно пользоваться следующими правилами:
1. По заданной функции алгебры логики построить таблицу истинности (таблица, в которой каждому набору значений переменных сопоставляется значение выходного сигнала, называется таблицей истинности функции).
2. Выписать все конституенты единицы, соединив их между собой знаком дизъюнкции.
Пусть дана функция
 .
Построим для нее таблицу истинности.
Для удобства определения ДСНФ функции
осуществим вычисления по действиям:
.
Построим для нее таблицу истинности.
Для удобства определения ДСНФ функции
осуществим вычисления по действиям:

х1 х2 х3 |
a
=
|
b
=
|
c
= |
d
=
a |
e = d/c |
000 |
1 |
1 |
0 |
1 |
1 |
001 |
1 |
0 |
0 |
0 |
1 |
010 |
1 |
0 |
0 |
0 |
1 |
011 |
1 |
1 |
0 |
1 |
1 |
100 |
1 |
1 |
1 |
1 |
0 |
101 |
0 |
0 |
1 |
1 |
0 |
110 |
1 |
0 |
0 |
0 |
1 |
111 |
0 |
1 |
0 |
0 |
1 |
ДСНФ функции
 .
.
Каждой функции алгебры логики можно поставить в соответствие комбинационную схему, её реализующую. Комбинационная схема состоит из базисных элементов, которые являются технической реализацией функций алгебры логики. Базисные элементы графически изображаются в виде прямоугольников, в которых инверсные входы и выход изображают в виде незаштрихованных кружков, в верхнем правом углу ставят 1, если этот элемент реализует функцию дизъюнкции, и & – если элемент реализует функцию конъюнкции, за исключением сложения по модулю 2 и эквивалентности (тогда сверху ставят = 1) (рис. 2а).
Более сложные элементы графически изображают в виде композиции перечисленных базисных элементов (рис. 2б).
Полученная ранее
ДСНФ функции, должна состоять из
инверторов, конъюнкторов и дизъюнктора,
реализующих отрицание, конъюнкцию и
дизъюнкцию соответственно. Количество
инверторов определяется числом различных
переменных, входящих в функцию со знаком
отрицания. В рассматриваемом примере
все три переменные
 входят в ДСНФ с отрицанием и, следовательно,
схема должна содержать три инвертора.
Количество конъюнкторов в схеме
определяется числом конституент единицы,
входящих в ДСНФ. В нашем примере их
шесть.
входят в ДСНФ с отрицанием и, следовательно,
схема должна содержать три инвертора.
Количество конъюнкторов в схеме
определяется числом конституент единицы,
входящих в ДСНФ. В нашем примере их
шесть.

Рис. 2. Графические изображения базисных элементов
Комбинационная схема, реализующая ДСНФ рассмотренной функции алгебры логики, показана на рисунке 3.
Элементарной
дизъюнкцией
называется дизъюнкция, в которую каждая
переменная входит только один раз, либо
с отрицанием, либо без него ( ). Число переменных дизъюнкции называется
рангом
элементарной дизъюнкции.
). Число переменных дизъюнкции называется
рангом
элементарной дизъюнкции.
Конъюнктивной
нормальной формой (КНФ)
называется конъюнкция элементарных
дизъюнкций (( ;
;
 и т. д.).
и т. д.).
Конституентой нуля называется конституента, на которой функция алгебры логики обращается в ноль.
Любая функция алгебры логики, кроме единицы, может быть представлена в следующей форме:

где
 ;
;
– степень переменной (если она равна 0, то переменная записывается в инверсной форме ( ), а если равна 1, то переменная записывается без отрицания ( )).

Рис. 3. Комбинационная схема, реализующая ДСНФ
заданной
функции

При этом конъюнкция в правой части (1) берется по тем наборам переменных, на которых функция, заданная таблицей истинности, обращается в ноль, т. е. берутся только конституенты нуля.
Представление функции алгебры логики в виде (1) называется конъюнктивной совершенной нормальной формой (КСНФ).
В итоге КСНФ – это КНФ, все дизъюнкции которой имеют один и тот же ранг, равный числу переменных функции.
Любая функция алгебры логики имеет единственную КСНФ. Для получения КСНФ функции алгебры логики удобно пользоваться следующими правилами:
1. По заданной функции алгебры логики построить таблицу истинности.
2. Выписать все конституенты нуля, соединив их между собой знаком конъюнкции.
Пусть дана функция . Построим для нее таблицу истинности. Для удобства определения КСНФ функции осуществим вычисления по действиям:
х1 х2 х3 |
a= |
b= |
c= |
d=a b |
e=d/c |
000 |
1 |
1 |
0 |
1 |
1 |
001 |
1 |
0 |
0 |
0 |
1 |
010 |
1 |
0 |
0 |
0 |
1 |
011 |
1 |
1 |
0 |
1 |
1 |
100 |
1 |
1 |
1 |
1 |
0 |
101 |
0 |
0 |
1 |
1 |
0 |
110 |
1 |
0 |
0 |
0 |
1 |
111 |
0 |
1 |
0 |
0 |
1 |
КСНФ функции
 .
.
Комбинационная схема, реализующая КСНФ рассмотренной функции алгебры логики, показана на рисунке 4.
Выбор той или иной формы записи функции алгебры логики (ДСНФ или КСНФ) определяется ее таблицей истинности. Если в таблице истинности заданной функции получилось больше конституент нуля, то выгодно записывать ДСНФ функции, в противном случае (если больше конституент единицы) – КСНФ.

Рис. 4. Комбинационная схема, реализующая КСНФ
заданной функции

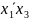


 b
b