МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Волгоградский государственный технический университет»

Кафедра «Вычислительная техника»

Методические указания

к выполнению семестрового задания по курсу

«Математическая логика и теория алгоритмов»

для студентов очной, очно-заочной, заочной форм обучения по направлениям «Информатика и вычислительная техника», «Приборостроение»

Волгоград

2018

УДК 510.6 (075)

Рецензент

канд. техн. наук доцент Андреев А.Е.

Издается по решению редакционно-издательского совета

Волгоградского государственного технического университета

Методические указания к выполнению семестрового задания по курсу

«Математическая логика и теория алгоритмов» для студентов очной, очно-заочной, заочной форм обучения по направлениям «Информатика и вычислительная техника», «Приборостроение» / сост. О. А. Авдеюк. ­–Волгоград: ИУНЛ ВолгГТУ, 2018. – 32 с.

Методические указания содержат варианты заданий для выполнения самостоятельной работы студентов. Набор задач охватывает основные разделы алгебры логики. Приведен пример оформления и решения работы.

Сборник предназначен для студентов всех форм обучения по направлениям подготовки бакалавров «Информатика и вычислительная техника», «Приборостроение», а также всех направление, изучающих курсы “Дискретная математика», «Математическая логика и теория алгоритмов».

© Волгоградский государственный

технический университет, 2018.

© О. А. Авдеюк, 2018.

1.МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Контрольная (семестровая) работа предполагает закрепление студентом полученных знаний по разделу “ Математическая логика» и содержит 30 вариантов заданий по 10 задач в каждом, тем самым предусматривается индивидуальная работа студента. Номер варианта для студентов безотрывных форм обучения равен сумме трех последних цифр зачетной книжки; для студентов очной формы – порядковому номеру в журнале группы.

В результате выполнения работ оформляется протоколы в тонкой ученической тетради (12 или 18 листов) по правилу, рассмотренному в нижеследующих примерах. Варианты заданий определяются преподавателем.

Пример оформления титульного листа

Тетрадь для выполнения контрольной (семестровой) работы по курсу «Математическая логика и теория алгоритмов». Вариант 31 Выполнил: студент ФЭВТ ВолгГТУ группы ИИТ-373 Петров В.А. Дата сдачи работы: 10.12.20__ г. Проверил: Баллы:

2. СБОРНИК ЗАДАНИЙ

2.1. Пример решения и оформления

1. Используя таблицу истинности, установить эквивалентность функций в формуле:

Решение:

Обозначим: f₁ = X₁  X₂

f₂ = f₃ = f₄ =

Составим таблицу истинности для правой и левой части функции:

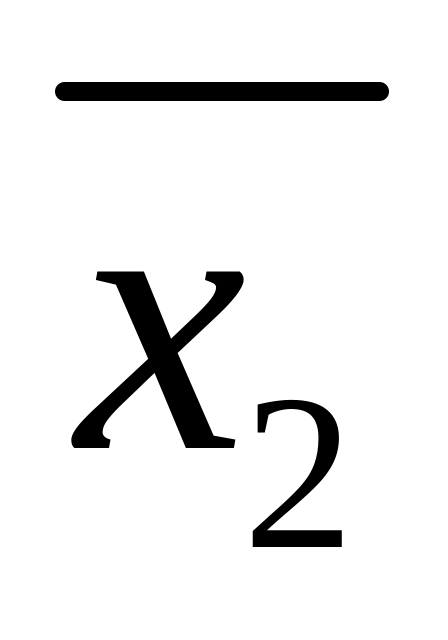х1 х2 f1	f2 f3 f4
0 0 0 0 1 1 1 0 1 1 1 0	1 1 1 1 0 1 1 0 0 1 0 0 1 1 1 0 1 0 1 0

Ответ: Как видно из таблицы, значения правой и левой части равенства действительно совпадают, значит, функции в данной формуле эквивалентны.

Ответ: х₁,х₂,х₃ – существенные переменные.

2. Используя основные законы и соотношения алгебры логики, необходимо установить справедливость следующей формулы:

Решение:

Рекомендация: Заданное соотношение необязательно эквивалентно, поэтому необходимо перед выполнением задания проверить истинность согласно задаче № 1.

1. Проверка справедливости заданного соотношения по таблице истинности.

Если равенство неверно, основная часть задачи далее не выполняется.

Иначе

2. Необходимо левую часть равенства привести к правой части равенства.

2.1.

2.2..х₁ \/ х₁х₂ = х₁ / по формуле склеивания /.

2.3. х₁ \/ = х₁ / по формуле поглощения /.

2.4. В результате в левой части равенства имеем: х₁ \/ ,что и требовалось доказать.

Ответ: соотношение в данной формуле справедливо.

3. Определить к каким классам (константы нуля, константы единицы, самодвойственных функций, монотонных функций, линейных функций, симметрических функций) относится функция следующего вида:

f(x₁,x₂,x₃) = x₁x₂ \/ .

Решение:

1. Составим таблицу истинности:

х1 х2 х3 x1&x2 x3&x2 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 0 1 1 0 1 0 1 0 0 0 0 1 1 0 1 0 0 1 1 1 0 1 0 1 1 1 1 1 1 0

f(x1,x2,x3) 1 1 1 0 1 1 1 1

2. Т. к. f(0,0,0)  0, значит, данная функция не относится к классу константы 0.

3. Т. к. f (1,1,1) = 1, значит, данная функция относится к классу константы 1.

4. Т. к. f(0,1,1) < f (0,1,0) и f(1,0,0) > f(0,1,1), значит, данная функция не относится к классу монотонных функций.

5. Т. к., например, f(0,0,0) = f(1,1,1) или f(0,0,1) = f(1,1,0), то данная функция не относится к классу самодвойственных функций.

6. Т. к. не выполняется условие f(0,1,1) = f(1,0,1) = f(1,1,0) / значения соответственно равны 0,1,1/, то данная функция не относится к классу симметрических функций.

7. Проверим принадлежность функции к классу линейных функций.

Для этого запишем ее в таком виде:

f₁(x₁,x₂,x₃) = C₀  C₁&X₁  C₂&X₂  C₃&X₃.

Найдем коэффициенты C_i :

f (0,0,0) = 1 / из таблицы истинности /

С₀  С₁&0  C₂&0 C₃&0 = 1 , т.о., С₀ = 1.

f(1,0,0 )=1 / из таблицы истинности /

1  C₁&1  C₂&0  C₃&0 = 1, т.о., С₁ = 0.

f(0,1,0) = 1/ из таблицы истинности /

1  C₁&0  C₂&1  C₃&0 = 1, т.о., С₂ = 0.

f(0,0,1) = 1 / из таблицы истинности /

1  C₁&0  C₂&0  C₃&1 = 1 ,т.о., С₃ = 0.

Тогда f₁(x₁,x₂,x₃) = 1.

Сравним значения функций f и f₁ по таблице истинности:

№ х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1

f(x1,x2,x3) 1 1 1 0 1 1 1 1

f1(x1,x2,x3) 1 1 1 1 1 1 1 1

Т. к. значения функций различны для одинаковых наборов, то данная функция не относится к классу линейных функций.

Ответ: данная функция относится к классу константы 1.

4. Необходимо для данной ФАЛ f(x₁,x₂,x₃) найти ее ДСНФ,КСНФ,ПСНФ,ЭСНФ,ИСНФ, принимающей значение 1 на следующих наборах: 0 , 4, 6, 7.

Решение:

1. Составим таблицу истинности:

№ х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1

f(x1,x2,x3) 1 0 0 0 1 0 1 1

2. Для получения ДСНФ, ПСНФ используем термы для 1 значений функции:

ДСНФ: f(x₁,x₂,x₃ ) =

ПСНФ: f(x₁,x₂,x₃)= .

3.Для получения КСНФ, ЭСНФ используем термы для 0 значений функции:

КСНФ: f(x₁,x₂,x₃) =

ЭСНФ: f(x₁,x₂,x₃) =

4. ИСНФ:

1. Для получения первой формы ИСНФ 1 используем термы для 1 значений функции:

f(x₁,x₂,x₃) = .

2. Для получения второй формы ИСНФ 0 используем термы для 0 значений функций:

f(x₁,x₂,x₃) =

4. Используя метод неопределенных коэффициентов, необходимо найти МДНФ функции f(x1,x2,x3), принимающей значение 1 на наборах:

0 , 5 , 7.

Решение:

1. Составим таблицу истинности:

№ х1 х2 х3 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 1 6 1 1 0 7 1 1 1

f(x1,x2,x3) 1 0 0 0 0 1 0 1

2.

К₁⁰ \/ К₂⁰ \/ К₃⁰ \/ К₁₂⁰⁰ \/ К₁₃⁰⁰ \/ К₂₃⁰⁰ \/ К₁₂₃⁰⁰⁰ = 1

К₁⁰ \/ К₂⁰ \/ К₃¹ \/ К₁₂⁰⁰ \/ К₁₃⁰¹ \/ К₂₃⁰¹ \/ К₁₂₃⁰⁰¹ = 0

К₁⁰ \/ К₂¹ \/ К₃⁰ \/ К₁₂⁰¹ \/ К₁₃⁰⁰ \/ К₂₃¹⁰ \/ К₁₂₃⁰¹⁰ = 0

К₁⁰ \/ К₂¹ \/ К₃¹ \/ К₁₂⁰¹ \/ К₁₃⁰¹ \/ К₂₃¹¹ \/ К₁₂₃⁰¹¹ = 0

К₁¹ \/ К₂⁰ \/ К₃⁰ \/ К₁₂¹⁰ \/ К₁₃¹⁰ \/ К₂₃⁰⁰ \/ К₁₂₃¹⁰⁰ = 0

К₁¹ \/ К₂⁰ \/ К₃¹ \/ К₁₂¹⁰ \/ К₁₃¹¹ \/ К₂₃⁰¹ \/ К₁₂₃¹⁰¹ = 1

К₁¹ \/ К₂¹ \/ К₃⁰ \/ К₁₂¹¹ \/ К₁₃¹⁰ \/ К₂₃¹⁰ \/ К₁₂₃¹¹⁰ = 0

К₁¹ \/ К₂¹ \/ К₃¹ \/ К₁₂¹¹ \/ К₁₃¹¹ \/ К₂₃¹¹ \/ К₁₂₃¹¹¹ = 1

3. Приравняем 0 все коэффициенты при 0 значениях функции:

К₁⁰ = К₂⁰ = К₃¹ = К₁₂⁰⁰ = К₁₃⁰¹ = К₂₃⁰¹ = К₁₂₃⁰⁰¹ = 0

К₁⁰ = К₂¹ = К₃⁰ = К₁₂⁰¹ = К₁₃⁰⁰ = К₂₃¹⁰ = К₁₂₃⁰¹⁰ = 0

К₁⁰ = К₂¹ = К₃¹ = К₁₂⁰¹ = К₁₃⁰¹ = К₂₃¹¹ = К₁₂₃⁰¹¹ = 0

К₁¹ = К₂⁰ = К₃⁰ = К₁₂¹⁰ = К₁₃¹⁰ = К₂₃⁰⁰ = К₁₂₃¹⁰⁰ = 0

К₁¹ = К₂¹ = К₃⁰ = К₁₂¹¹ = К₁₃¹⁰ = К₂₃¹⁰ = К₁₂₃¹¹⁰ = 0.

4. Вычеркнем 0 коэффициенты из коэффициентов при 1 значениях функции:

К₁₂₃⁰⁰⁰ = 1

К₁₃¹¹ \/ К₁₂₃¹⁰¹ = 1

К₁₂¹¹ \/ К₁₃¹¹ \/ К₁₂₃¹¹¹ = 1

5. Найдем минимальное покрытие: К₁₂₃⁰⁰⁰ и К₁₃¹¹ ,т. е.

f₁(x₁,x₂,x₃) =