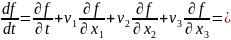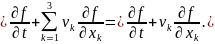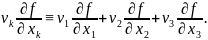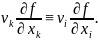- •6.2 Механические свойства горных пород 50
- •1 Предмет и методы механики сплошных сред. Некоторые сведения о векторном анализе
- •Основные гипотезы механики сплошных сред
- •Некоторые сведения о векторном анализе
- •Компоненты векторов в декартовой системе координат. Индексные обозначения
- •Градиент
- •Поток вектора
- •Дивергенция
- •Циркуляция
- •2 Два подхода к описанию движения сплошной среды
- •2.1 Пространственные и материальные координаты
- •2.2 Закон движения сплошной среды
- •2.3 Лагранжев и Эйлеров подходы к описанию движения сплошной среды
- •Переход от лагранжева описания к эйлерову
- •Переход от эйлерова описания к лагранжеву
- •2.4 Материальная (индивидуальная, полная) производная по времени
- •2.5 Линии тока и траектории
- •2.6 Установившееся и неустановившееся движение
- •Силы в сплошной среде. Тензор напряжения
- •3.1 Силы, действующие на сплошную среду. Вектор напряжения
- •4.2 Тензор напряжений
- •4 Элементы теории деформаций
- •4.1 Тензор деформаций
- •3.2 Механический смысл компонент тензора деформаций
- •3.3 Выражение тензора деформаций через вектор перемещений
- •3.4 Тензор скоростей деформаций. Вектор вихря
- •5 Законы сохранения и универсальные уравнения механики сплошных сред
- •5.1 Закон сохранения массы и уравнение неразрывности
- •Уравнение неразрывности для несжимаемой среды
- •5.2 Понятие математической модели среды. Универсальные уравнения и определяющие соотношения
- •5.3 Модель идеальной жидкости/газа
- •5.4 Полная система уравнений идеальной жидкости
- •Граничное условие на поверхности твердых тел для идеальной жидкости
- •5.4 Несжимаемая идеальная жидкость. Полная система уравнений
- •5.5 Модель вязкой жидкости
- •6 Механические свойства горных пород
- •6.1 Механические свойства твердых тел и их показатели
- •6.2 Механические свойства горных пород
- •6.3 Классификация горных пород по механическим свойствам
- •6.4 Естественное напряженное состояние горных пород и его изменение вблизи горных выработок
- •6.5 Деформация горных пород вблизи скважины Упругая деформация
- •Пластическая деформация
- •7 Взаимодействие горных пород и насыщающих их жидкостей
- •7.1 Основные представления о механическом взаимодействии горных пород и насыщающих их жидкостей
- •7.2 Деформация горных пород в результате механического взаимодействия горных пород и насыщающих их жидкостей
- •Упругая деформация
- •Пластическая деформация
- •7.3 Механическое взаимодействие горных пород и фильтрующейся жидкости при упругом режиме пластов
- •8.1 Вертикальные трещины Вертикальные трещины с линейным распределением давления
- •Вертикальные трещины с параболическим распределением давления
- •8.2 Осесимметричные горизонтальные трещины Горизонтальные трещины с линейным распределением давления
- •Горизонтальные трещины с параболическим распределением давления
- •8.3 Закачка нефильтрующейся жидкости Образование горизонтальной трещины в результате закачки нефильтрующейся жидкости
- •Образование вертикальной трещины в результате закачки нефильтрующейся жидкости
- •8.4 Закачка фильтрующейся жидкости
2.4 Материальная (индивидуальная, полная) производная по времени
Материальная
или индивидуальная производная по
времени
от величины
 описывает,
как меняется со временем величина
в индивидуальной точке среды. Обычно в
механике сплошных сред индивидуальная
производная функции
обозначается
описывает,
как меняется со временем величина
в индивидуальной точке среды. Обычно в
механике сплошных сред индивидуальная
производная функции
обозначается
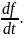
Как
вычисляется индивидуальная производная
по
,
если
задана по способу Лагранжа, то есть
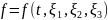 ?
Так как для индивидуальной точки
?
Так как для индивидуальной точки
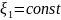 ,
,
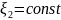 ,
,
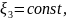 то очевидно, индивидуальная производная
то очевидно, индивидуальная производная
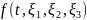 есть просто частная производная по
времени
:
есть просто частная производная по
времени
:
|
|
(2.7) |
Здесь
символом
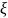 обозначен набор
.
обозначен набор
.
Какие
надо проводить измерения, чтобы найти
индивидуальную производную
по
?
Надо иметь прибор, который следит за
индивидуальной частицей, например,
движется вместе с ней и измеряет
в этой частице (рисунки 2.1 и 2.2). Для
измерения величины индивидуальной
производной в данной точке А
в момент времени
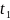 в той частице, которая находится в этот
момент в точке А,
затем в близкий момент
в той частице, которая находится в этот
момент в точке А,
затем в близкий момент
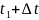 измерить
в той же самой индивидуальной частице
(которая в этот момент находится уже не
в точке А,
а в точке В!)
и разность полученных значений разделить
на
измерить
в той же самой индивидуальной частице
(которая в этот момент находится уже не
в точке А,
а в точке В!)
и разность полученных значений разделить
на
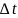 :
:
|
|
(2.8) |

Рисунок 2.2 – Измерение значения индивидуальной производной в материальной точке
Как
вычисляется индивидуальная производная
по
,
если
задана по способу Эйлера, то есть
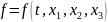 ?
Вычислим сначала частную производную
по
при постоянных
,
то есть величину
?
Вычислим сначала частную производную
по
при постоянных
,
то есть величину
 .
Что она описывает? Она описывает изменение
со временем в фиксированной точке
пространства; поэтому
называется локальной производной
по времени. Если среда движется, то в
рассматриваемой точке пространства в
разные моменты времени находятся разные
индивидуальные точки среды. Приближенное
значение
в точке А
измеряется
так (рис. 2.3):
.
Что она описывает? Она описывает изменение
со временем в фиксированной точке
пространства; поэтому
называется локальной производной
по времени. Если среда движется, то в
рассматриваемой точке пространства в
разные моменты времени находятся разные
индивидуальные точки среды. Приближенное
значение
в точке А
измеряется
так (рис. 2.3):
|
|
(2.9) |

Рисунок 2.3 – Измерение значения локальной производной в точке А в момент времени
Поэтому для индивидуальной точки является сложной функцией времени: зависит от , и , а зависят от и , и индивидуальная производная вычисляется как производная сложной функции
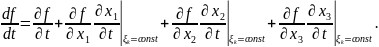
Далее, производные по времени от координат при постоянных есть компоненты скорости частицы
|
|
(2.10) |
Поэтому выражение для индивидуальной производной при эйлеровом описании таково
|
|
(2.11) |
В последнем выражении использовано следующее соглашение о суммировании (правило Эйнштейна): если в одночлене какой-то индекс повторяется дважды, то по этому индексу производится суммирование от 1 до 3, а знак суммы не пишется, то есть
|
|
(2.12) |
Отметим, что обозначение индекса суммирования при этом не существенно,
|
|
(2.13) |
2.5 Линии тока и траектории
Понятие линий тока используется при эйлеровом описании движения среды, в основном при описании движения жидкостей и газов.
Линия тока - это линия, которая определяется для фиксированного момента времени и обладает тем свойством, что в каждой ее точке направление касательной совпадает с направлением вектора скорости среды. Отметим, что в рассматриваемый момент времени в разных точках линии тока находятся разные частицы.
Понятие траектории связано с лагранжевым подходом к описанию движения.
Траектория – это путь индивидуальной частицы; в каждой точке траектории направление касательной к траектории совпадает с направлением вектора скорости. Но здесь имеется в виду скорости одной и той же частицы в разные моменты времени, в то время как, говоря о линии тока, мы рассматриваем скорости разных частиц в один и тот же момент времени.

Рисунок 2.5 –
Сплошная линия – линия тока в момент
времени
 пунктир – траектория точки А
пунктир – траектория точки А

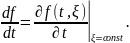
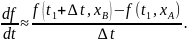
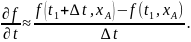
 .
.