Некоторые сведения о векторном анализе
Все физические величины можно разделить на три группы: скаляры, векторы и тензоры.
Скаляр – это величина, каждое значение которой может быть выражено одним числом.
Векторной величиной называется величина, представляющая собой одновременно и число, и направление (скорость, ускорение).
Тензор – это объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются скаляры (тензор нулевого ранга), векторы (тензор первого ранга), матрицы (тензор второго ранга) и т.п.
Компоненты векторов в декартовой системе координат. Индексные обозначения
В
декартовой системе координат компоненты
вектора – это величины проекций вектора
на координатные оси. Обычно координаты
обозначаются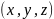
,
а единичные векторы, направленные вдоль
осей координат (векторы базиса), –
.
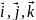Тогда, компоненты вектора
будем обозначать как
.
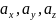Следовательно, справедлива запись:
.
Часто
имеют место так называемые индексные
обозначения. Координаты обозначаются
как
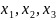(предполагается, что
,
,
).
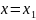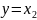Векторы базиса при этом обозначаются
,
а компоненты вектора
-
.
Тогда вектор
можно записать в виде:
.
Существует
удобное правило для краткой записи сумм
такого вида, называемое правилом
Эйнштейна: если в одночленном выражении
с буквенными индексами два индекса
совпадают, то считается, что по этим
индексам производится суммирование, а
знак
опускается. Таким образом, вместо
,
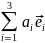используется запись
.
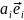Скалярным
произведением
двух векторов
и
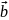называется число, обозначаемое
и равное произведению длин векторов
,
и косинуса угла
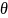между ними:
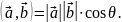
Примечание: В декартовой ортогональной системе координат скалярное произведение двух векторов равно сумме произведений их соответствующих компонент:
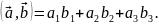
Длина вектора определяется по формуле:
Величина
проекции
вектора
на направление, задаваемое единичным
вектором
,
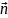равна скалярному произведению
:
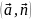Векторным
произведением
двух векторов
и
называется вектор, обозначаемый
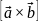и
перпендикулярный
векторам
и
и направленный так, что с его конца
переход от
к
происходит против часовой стрелки.
Длина
этого вектора равна площади параллелограмма,
построенного на векторах
и
.
Для векторов базиса ортогональной
декартовой системы координат имеем:
,
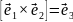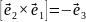и т.д. Поэтому векторное произведение
в декартовой системе координат
представляется в виде следующего
определителя:
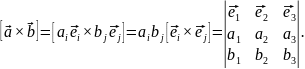
Если некоторая величина задана во всех точках рассматриваемой области, то можно говорить о поле этой величины. Например, поле скорости – это совокупность скоростей всех точек среды в рассматриваемой области.
Предположим,
что в каждой точке
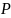некоторой области
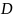нами задано значение скалярной физической
величины
,
т.е. такой величины, которая полностью
характеризуется своим числовым значением.
Например, это
может быть температура точек неравномерно
нагретого тела, плотность распределения
электрических зарядов в изолированном
теле, потенциал электрического поля
и т.д. При этом
называется скалярной
функцией
точки; записывается это так:
.
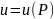Если
в области
задана скалярная функция точки
,
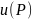то говорят, что в этой области задано
скалярное
поле.
Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении.
Производной
функции
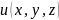по направлению
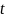в точке
называется предел:
