2. Проекции отрезка прямой линии. Прямые общего и частного положения

Из геометрии известно, что однозначно положение прямой в пространстве определяют две точки. Предположим, что даны горизонтальные, фронтальные и профильные проекции точек А и В. Проведя через них одноименные проекции линии, получим горизонтальную А'В', фронтальную А"В" и профильную А"'В"' проекции прямой АВ (рис.6).

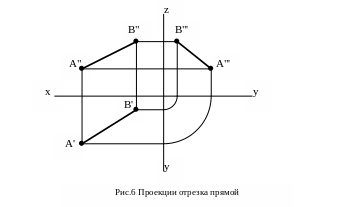
Можно ли утверждать, что этот чертеж выражает именно отрезок прямой? Если через А'В' и А"В" провести проецирующие плоскости ₁ и ₂ соответственно, то в их пересечении получается прямая и её отрезок АВ (рис.7).

Рис.7 Отрезок прямой АВ и его проекции

Точки А и В находятся на разных расстояниях от плоскостей ₁, ₂ и ₃. Таким образом очевидно, что прямая АВ не параллельна ни одной из плоскостей проекций. При этом её проекции не параллельны и не перпендикулярны ни одной из осей. Такая прямая называется прямой общего положения.

1. Прямые частного положения

Наряду с прямыми общего положения существуют прямые, расположенные особым образом относительно плоскостей проекций. Их называют прямыми частного положения и подразделяют на следующие виды:

Прямые, параллельные одной из плоскостей проекций:

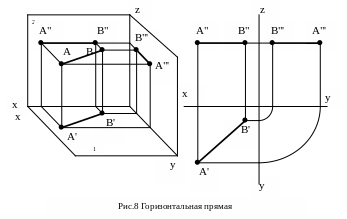
Горизонтальная прямая (рис.8) – это прямая, параллельная горизонтальной плоскости проекций ₁. Её фронтальная проекция всегда параллельна оси ОХ, а горизонтальная представляет собой натуральную величину отрезка.

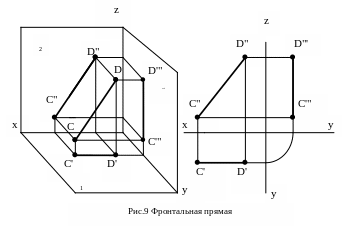
Фронтальная прямая (рис.9) – это прямая, параллельная фронтальной плоскости проекций. Её горизонтальная проекция всегда параллельна оси ОХ, а фронтальная равна натуральной величине заданного отрезка.

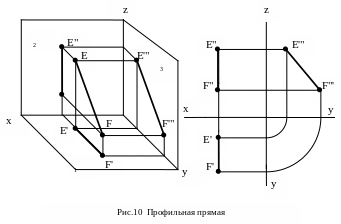
Профильная прямая (рис.10) – это прямая, параллельная профильной плоскости проекций. Её профильная проекция представляет собой натуральную величину, а горизонтальная и фронтальная всегда перпендикулярны оси ОХ.

Прямые, параллельные двум плоскостям проекций:

Горизонтально-проецирующая прямая (рис.11) – это прямая, параллельная фронтальной ₂ и профильной ₃ плоскостям проекций и перпендикулярная горизонтальной плоскости проекций. При этом на плоскость ₁ она проецируется в точку. Фронтальная и профильная проекции прямой являются натуральной величиной отрезка прямой.

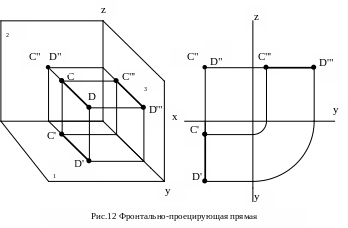
Фронтально-проецирующей прямой (рис.12) называется прямая, параллельная горизонтальной ₁ и профильной ₃ плоскостям проекций и перпендикулярная фронтальной плоскости проекций ₂. При этом её горизонтальная и профильная проекции представляют собой натуральную величину отрезка, а фронтальная является точкой.

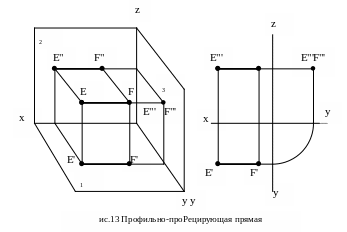
Профильно-проецирующая прямая (рис.13) – это прямая, перпендикулярная профильной плоскости проекций ₃ и параллельная горизонтальной ₁ и фронтальной ₂ плоскостям проекций. При этом на профильную плоскость проекций она проецируется в точку, а на две другие – в свою натуральную величину.