
- •Оглавление
- •Введение
- •§1. Метрические пространства. Примеры
- •§2. Сходимость в метрическом пространстве
- •§3. Полнота, неполнота, пополнение (пространств)
- •§4. Функции. Принцип сжимающихся отображений
- •§5. Дифференцируемость
- •§6. Градиент. Производная по направлению. Необходимые условия локального экстремума
- •§7. Производная сложной функции
- •§8. Дифференциал. Касательная плоскость. Нормаль поверхности.
- •§9. Условие Коши-Римана
- •§10. Достаточные условия дифференцируемости
- •§11. Производные и дифференциалы высших порядков
- •§12. Теорема о конечном приращении
- •§13. Ряд и формула Тейлора
- •§14. Экстремум функций многих переменных
- •§15. Условный экстремум
- •Вопросы к коллоквиуму
- •Литература
§11. Производные и дифференциалы высших порядков
Рассмотрим
отображение
 .
Если оно дифференцируемо, то
.
Если оно дифференцируемо, то
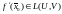 .
Будем считать, что производная задана
не в отдельной точки, а на всём
или в некоторой его подобласти. Учитывая
изменение производной от точки к точке,
получаем отображение
.
Будем считать, что производная задана
не в отдельной точки, а на всём
или в некоторой его подобласти. Учитывая
изменение производной от точки к точке,
получаем отображение
 .
Данное отображение, в свою очередь, тоже
может быть дифференцируемым, его
производная называется второй производной
исходного отображения, при этом
.
Данное отображение, в свою очередь, тоже
может быть дифференцируемым, его
производная называется второй производной
исходного отображения, при этом
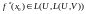 .
Такую процедуру можно продолжить и
получить
.
Такую процедуру можно продолжить и
получить
 .
.
Рассмотрим случай
скалярной функции нескольких переменных
 .
Условие дифференцируемости её производной
запишется виде
.
Условие дифференцируемости её производной
запишется виде
 ,
при этом второе слагаемое называется
вторым дифференциалом
,
при этом второе слагаемое называется
вторым дифференциалом
 .
Он является величиной
более высокого порядка малости, чем
первое
.
Он является величиной
более высокого порядка малости, чем
первое
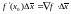 ,
если оно не обращается в ноль.
,
если оно не обращается в ноль.
Вспомним, что
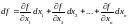 ,
тогда
,
тогда
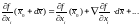 ,
,
где вектор
 имеет координаты
имеет координаты
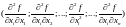 ,
таким образом,
,
таким образом,
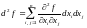 .
Как мы далее увидим, при достаточно
естественных предположениях, эта
квадратичная форма является симметричной.
.
Как мы далее увидим, при достаточно
естественных предположениях, эта
квадратичная форма является симметричной.
Теорема. Если в некоторой точке существуют непрерывные смешанные производные, то они не зависят от порядка дифференцирования.
Доказательство.
Проведём
доказательство для второй производной
функции двух переменных
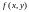 .
В дальнейших выкладках использован тот
факт, что существование вторых производных
влечёт непрерывность первых в некоторой
окрестности рассматриваемой точки.
.
В дальнейших выкладках использован тот
факт, что существование вторых производных
влечёт непрерывность первых в некоторой
окрестности рассматриваемой точки.
Пусть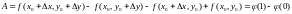 ,
,
где
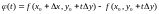 .
.
Тогда, по теореме Лагранжа,
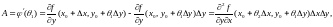
где
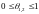 .
В то же время,
.
В то же время,
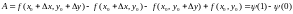 ,
,
где
 .
Тогда, по теореме Лагранжа,
.
Тогда, по теореме Лагранжа,
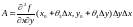 ,
где
.
,
где
.
Так как число – одинаковое в обоих случаях, мы получаем равенство
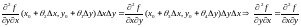 .
.
Случай производных произвольного порядка вытекает из приведённых выше рассуждений и определения производных высших порядков.
§12. Теорема о конечном приращении
Для дальнейшего,
хотелось бы получить аналог формулы
Лагранжа ,
но его в многомерном случае получить
не удаётся. Однако удаётся получить
обобщение его следствия.
,
но его в многомерном случае получить
не удаётся. Однако удаётся получить
обобщение его следствия.
Теорема о конечном
приращении.
Пусть во всех точках отрезка
 в банаховом пространстве задано
дифференцируемое отображение
в банаховом пространстве задано
дифференцируемое отображение
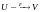 ,
причём во всех точках данного отрезка
выполняется неравенство
,
причём во всех точках данного отрезка
выполняется неравенство
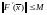 ,
тогда
,
тогда
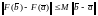 .
.
Доказательство.
Пусть
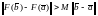 ,
тогда, для достаточно малого
,
будет выполняться неравенство
,
тогда, для достаточно малого
,
будет выполняться неравенство
 .
.
Разделим отрезок
пополам. Так как
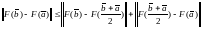 ,
найдётся такая половина отрезка, для
которой
,
найдётся такая половина отрезка, для
которой
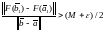 ,
т.е.
,
т.е.
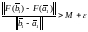 .
.
Продолжая эту
процедуру, получаем последовательность
вложенных друг в друга отрезков
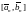 ,
для которых
,
для которых
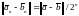 и выполняется
и выполняется
неравенство
 .
.
Расстояние между
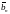 и
и
 – стремится к нулю, следовательно, в
силу
– стремится к нулю, следовательно, в
силу
замкнутости
отрезка
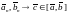 .
.
В силу дифференцируемости
отображения в точке
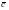 ,
можем записать
,
можем записать
 ,
,
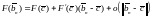 ,
откуда
,
откуда
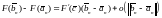 ,
так как
,
так как
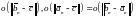 в силу того, что
в силу того, что
 .
.
Таким образом, должно выполняться неравенство:
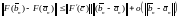 ,
откуда
,
откуда
 для достаточно
больших
.
Получилось противоречие, из которого
и следует требуемое утверждение.
для достаточно
больших
.
Получилось противоречие, из которого
и следует требуемое утверждение.
Теорема доказана.
§13. Ряд и формула Тейлора
Ряд Тейлора для функции одной переменной имеет вид:
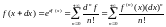 .
.
Для многомерного случая эта формула записывается аналогично:

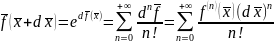
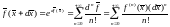 ,
,
где использовано
обозначение
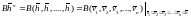 .
.
Формула Тейлора,
по аналогии с одномерным случаем,
запишется в виде:
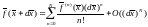 .
.
Введём обозначение
 ,
тогда последнюю формулу можно записать
в виде
,
тогда последнюю формулу можно записать
в виде
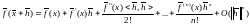 .
.
Вычислим производную
оператора
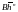 :
:
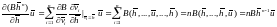 .
Здесь мы воспользовались симметричностью
оператора производной, которая следует
из независимости частных производных
от порядка
.
Здесь мы воспользовались симметричностью
оператора производной, которая следует
из независимости частных производных
от порядка
дифференцирования.
Для доказательства
формулы Тейлора надо доказать, что
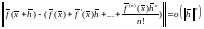 .
Доказательство проведём по методу
математической индукции. База индукции
следует из непрерывности отображения
.
Пусть
.
Доказательство проведём по методу
математической индукции. База индукции
следует из непрерывности отображения
.
Пусть
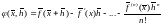 ,
тогда норма, которую нужно оценить,
равна
,
тогда норма, которую нужно оценить,
равна
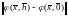 .
Но
.
Но
 по индуктивному предположению. Применяем
его к
по индуктивному предположению. Применяем
его к
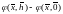 ,
используя теорему о конечном приращении
и приведённую выше формулу для
,
используя теорему о конечном приращении
и приведённую выше формулу для
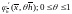 ,
получаем требуемую оценку.
,
получаем требуемую оценку.
