
- •Оглавление
- •Введение
- •§1. Метрические пространства. Примеры
- •§2. Сходимость в метрическом пространстве
- •§3. Полнота, неполнота, пополнение (пространств)
- •§4. Функции. Принцип сжимающихся отображений
- •§5. Дифференцируемость
- •§6. Градиент. Производная по направлению. Необходимые условия локального экстремума
- •§7. Производная сложной функции
- •§8. Дифференциал. Касательная плоскость. Нормаль поверхности.
- •§9. Условие Коши-Римана
- •§10. Достаточные условия дифференцируемости
- •§11. Производные и дифференциалы высших порядков
- •§12. Теорема о конечном приращении
- •§13. Ряд и формула Тейлора
- •§14. Экстремум функций многих переменных
- •§15. Условный экстремум
- •Вопросы к коллоквиуму
- •Литература
§4. Функции. Принцип сжимающихся отображений
Рассмотрим функции
(однозначные отображения) из одного
метрического пространства в другое:
 ,
т.е. ставящие в соответствие каждому
элементу из
,
т.е. ставящие в соответствие каждому
элементу из
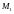 единственный элемент из
единственный элемент из
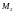 .
.
Замечание. Подмножество метрического пространства является метрическим пространством относительно той же метрики, при этом замкнутое подмножество полного метрического пространства является полным.
Можно ввести понятие предела функции.
Определение.
Говорят, что
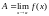 ,
когда для
,
когда для
 такое,
что если
такое,
что если
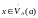 то
то
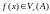 .
.
Напомним, что
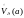 (проколотая
окрестность точки
)
это
(проколотая
окрестность точки
)
это
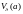 без самой точки
.
без самой точки
.
Упражнение. Чем это определение отличается от одномерного случая?
Определение.
Отображение
функции называется непрерывным,
если
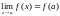 .
.
Упражнение. Какие результаты из одномерной теории пределов функций и теории непрерывных функций переносятся на случай отображений метрических пространств?
Для решения уравнений в метрических пространствах и для других разделов, например, для теории дифференциальных уравнений, важной является теорема о сжимающем отображении.
Определение.
Отображение
из одного метрического пространства в
другое называется сжимающим,
если существует такое число
 ,
что для любых
,
что для любых
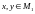 выполняется неравенство
выполняется неравенство
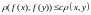 .
.
Определение.
Неподвижная
точка отображения
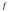 множества в себя это точка
множества в себя это точка
 ,
для которой выполнено равенство
,
для которой выполнено равенство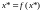 .
.
Теорема. Сжимающее отображение полного метрического
пространства в себя имеет единственную неподвижную точку.
Доказательство.
Пусть
– полное
метрическое пространство,
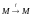 – сжимающее
отображение. Возьмём
– сжимающее
отображение. Возьмём
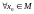 .
Построим
последовательность
.
Построим
последовательность
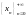 в
с
помощью рекуррентного соотношения
в
с
помощью рекуррентного соотношения
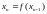 ,
т.е.
,
т.е.

Надо доказать, что данная последовательность будет сходящейся и что её предел будет неподвижной точкой отображения .
Существование
предела докажем, опираясь на полноту
пространства, т.е. нужно доказать, что
последовательность является
фундаментальной. Оценим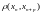 .
По неравенству треугольника можно
записать:
.
По неравенству треугольника можно
записать:
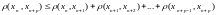
Воспользуемся тем, что отображение сжимающее.
 ,
,
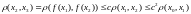 ,
,
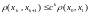 ,…,
,…,
откуда
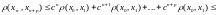
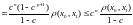 .
.
Таким образом, для
любого
существует
такое
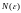 ,
что для всех
,
что для всех
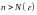 выполняется
неравенство
выполняется
неравенство
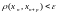 ,
т.е. последовательность
фундаментальна, поэтому должна сходится
к некоторой точке
,
т.е. последовательность
фундаментальна, поэтому должна сходится
к некоторой точке
 .
.
Докажем, что это
неподвижная точка. Используем неравенство
треугольника
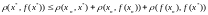 .
Первое слагаемое в правой части
неравенства стремится к нулю, так как
– предел последовательности
,
второе – так как
.
Первое слагаемое в правой части
неравенства стремится к нулю, так как
– предел последовательности
,
второе – так как
 ,
а для последнего имеем неравенство
,
а для последнего имеем неравенство
 ,
поэтому оно тоже стремиться к нулю.
,
поэтому оно тоже стремиться к нулю.
Таким образом,
число
 должно стремиться к 0 при
должно стремиться к 0 при
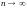 ,
но оно не зависит от
,
поэтому должно равняться нулю, откуда
,
т.е.
– неподвижная точка.
,
но оно не зависит от
,
поэтому должно равняться нулю, откуда
,
т.е.
– неподвижная точка.
Докажем, что эта
точка единственная. Предположим, что
существуют две неподвижные точки: x
и y.
Из свойства сжимаемости мы имеем
 ,
но
,
но
 ,
,
 ,
так как эти точки – неподвижные, поэтому
должно выполняться неравенство
,
так как эти точки – неподвижные, поэтому
должно выполняться неравенство
 ,
откуда
,
откуда
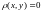 ,
т.е.
,
т.е.
 .
.
Теорема доказана.
Неподвижная точка
в практических применениях даёт решение
уравнения
.
Например, если идёт речь о дифференцируемой
функции одного переменного, то можно
записать равенство
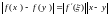 .
.
Таким образом,
если на некотором промежутке выполняется
неравенство
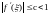 ,
и если
,
и если
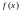 отображает
этот промежуток в себя, то существует
неподвижная точка y
этого отображения, при этом она
единственная и может быть найдена
методом последовательных приближений.
отображает
этот промежуток в себя, то существует
неподвижная точка y
этого отображения, при этом она
единственная и может быть найдена
методом последовательных приближений.
Пример:
Рассмотрим функцию
 на промежутке
на промежутке
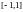 .
Легко видеть, что данная функция
отображает промежуток в себя и на нём
.
Легко видеть, что данная функция
отображает промежуток в себя и на нём
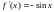 ,
откуда следует, что отображение сжимающее
с
,
откуда следует, что отображение сжимающее
с
 .
Следовательно, применима теорема, т.е.
на данном промежутке существует
единственное решение уравнения решения
.
Следовательно, применима теорема, т.е.
на данном промежутке существует
единственное решение уравнения решения
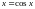 ,
которое может быть сколь угодно приближено
с помощью последовательных приближений
,
которое может быть сколь угодно приближено
с помощью последовательных приближений
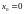 ,
,
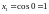 ,
,
 ,
,
 и т.д.
и т.д.
Упражнение. Оценить точность - го приближения.
