_{Министерство образования и науки Российской Федерации}

САНКТ – ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Д.А. Тархов, А.М. Никулин, Т.А. Шемякина

МАТЕМАТИКА

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

Учебное пособие

Санкт-Петербург

Издательство СПбГПУ

2013

Д.А. Тархов, А.М. Никулин, Т.А. Шемякина. Математика. Дифференциальное исчисление функций многих переменных: учебное пособие/ Д.А. Тархов, А.М. Никулин, Т.А. Шемякина. − СПб.: – Изд-во Политехн. ун-та, 2013. − 34 с.

Учебное пособие соответствует содержанию Федерального Государственного образовательного стандарта высшего профессионального образования дисциплины «Высшая математика» направления подготовки и переподготовки бакалавров по специальности 280700.62 «Техносферная безопасность».

В пособии кратко изложены теоретические основы дифференциального исчисления функций многих переменных по курсу "Высшая математика". Приведены многочисленные примеры с методическими рекомендациями по их решению.

Предназначено для студентов высших учебных заведений технических и экономических направлений, изучающих дисциплину «Высшая математика». Пособие может быть использовано при подготовке бакалавров, магистров, аспирантов и в системе дополнительного профессионального образования, а также оно будет полезно для преподавателей дневных, вечерних и заочных отделений вузов и технических университетов.

Библиогр.: 5 назв.

Печатается по решению редакционно-издательского совета факультета «Комплексная безопасность» Санкт-Петербургского государственного политехнического университета.

© Санкт- Петербургский государственный

политехнический университет, 2013

Оглавление

ВВЕДЕНИЕ………….…………………………….………………………..4

§1. Метрические пространства. Примеры……….………………………..5

§2. Сходимость в метрическом пространстве……..………………….…6

§3. Полнота, неполнота, пополнение (пространств)……..…………….....8

§4. Функции. Принцип сжимающихся отображений…………….……..14

§5. Дифференцируемость……………………………...……………………16

§6. Градиент. Производная по направлению. Необходимые условия…

локального экстремума…………………….………………….………….19

§7. Производная сложной функции……………………………………….21

§8. Дифференциал Касательная плоскость. Нормаль поверхности…22

§9. Условие Коши-Римана…………………….………………….……….23

§10. Достаточное условие дифференцируемости……………….……….24

§11. Производные и дифференциалы высших порядков…….……….25

§12. Теорема о конечном приращении…….……………………………27

§13. Ряд и формула Тейлора…….………………………………………..28

§14. Экстремум функций многих переменных….……………………..29

§15. Условный экстремум…….…………………………………………..32

Вопросы к коллоквиуму………………………………………….……...33

ЛИТЕРАТУРА……………….………………………………………….....34

Введение

Математический анализ составляет важнейшую часть основы высшей математики. Данное учебное пособие посвящено системному изучению начальных понятий математического анализа.

Целью данного пособия является помощь в усвоении математики, развитие навыков и умения в решении студентами задач математического анализа по указанным в нем темам в объеме действующих программ курса высшей математики.

В пособии кратко изложены теоретические основы дифференциального исчисления функций многих переменных по курсу «Математический анализ». При изложении теории приведены многочисленные примеры с методическими рекомендациями по их решению.

В пособии содержатся теоретические вопросы для подготовки к коллоквиуму по разделу «Дифференциальное исчисление функций многих переменных».

§1. Метрические пространства. Примеры

Дифференциальное исчисление опирается на теорию пределов, а теория пределов – на понятие ε - окресности, а понятие ε - окресности – на расстояние между точками. В связи с этим, прежде чем обобщать эти понятия, рассмотрим самое общее определение расстояния или метрики.

Определение. Метрическим пространством называется множество 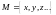, на котором введена неотрицательная функция двух переменных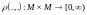 , которая удовлетворяет следующим свойствам:

1. .

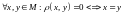2. Симметричность .

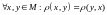3. Неравенство треугольника: ,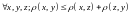

где 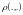называется метрикой (расстоянием).

Примеры:

1⁰. Если 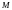– множество вещественных чисел 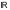, то в качестве метрики можно взять или _.

2⁰. Для 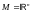, 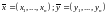обычно применяют одну из трёх основных метрик:

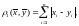
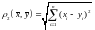и .

Заметим, что – евклидова метрика (обычное расстояние). Данное пространство является основным примером для дальнейших рассмотрений.

3⁰. 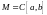– (множество функций, непрерывных на отрезке [a,b]). На этом множестве обычно вводят одну из следующих трёх метрик для :

.

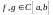Замечание. Определение подходит как для вещественнозначных, так и для комплекснозначных функций.

Упражнение. Проверить выполнение свойств метрики 1⁰ – 3⁰.