2.4. Компьютерные технологии начальной статистической обработки
ИСПОЛЬЗОВАНИЕ ВСТРОЕНЫХ СТАТИСТИЧЕСКИХ ФУНКЦИЙ И ПАКЕТА АНАЛИЗА Microsoft Excel.. В программе Microsoft Excel представлено большое число встроенных статистических функций. С их помощью можно рассчитать все обычно используемые на практике статистические характеристики. Для вызова нужной встроенной статистической функции используется команда Вставка ® Функция … или кнопка Вставка функции и появившемся окне Мастер функций
выбрать категорию «статистические» и указать нужную функцию в подокне выберете функцию. После выбора и щелчка по кнопке OK появляется окно Аргументы функции, с помощью которого осуществляется ввод адресов ячеек таблицы со значениями обрабатываемого массива и, при необходимости, других требуемых величин (например, степеней свободы).
Для построения гистограммы используется команда Сервис ® Анализ данных, после чего в появившемся окне Анализ данных
выбирается инструмент анализа – Гистограмма. В окне Гистограмма
задаются входной интервал, где указываются адреса ячеек с исходными данными, и интервал карманов, где указываются адреса ячеек со значениями границ интервалов. Также задаются желаемые параметры вывода щелкается кнопка OK.
Пример 2.4.1.. Рассчитать статистические характеристики и построить гистограмму по исходным данным, приведенным в таблице 2.2.1.
Решение с помощью Microsoft Excel. Для расчета основных статистических характеристик: среднего арифметического , медианы, моды, эмпирической дисперсии s2 и размаха, введем в ячейки таблицы исходные данные и используем встроенные статистические функции. Результаты расчета сведены в таблицу 2.5.1.
Tаблица 2.5.1
СРЗНАЧ |
МЕДИАНА |
МОДА |
ДИСП |
МИН |
МАКС |
916,4847 |
923,34109 |
944,78 |
9261,165 |
666,5183 |
1114,73 |
Для построения гистограммы используем команду Сервис ® Анализ ® Гистограмма. В окне Гистограмма задаем входной интервал, где указываем адреса ячеек с исходными данными, и интервал карманов, где указываем адреса ячеек со значениями границ интервалов. Выводятся таблица частот и гистограмма (рис. 2.5.1).
Карман |
Частота |
650 |
0 |
700 |
3 |
750 |
2 |
800 |
6 |
850 |
12 |
900 |
20 |
950 |
21 |
1000 |
17 |
1050 |
13 |
1100 |
4 |
1150 |
2 |
Еще |
0 |
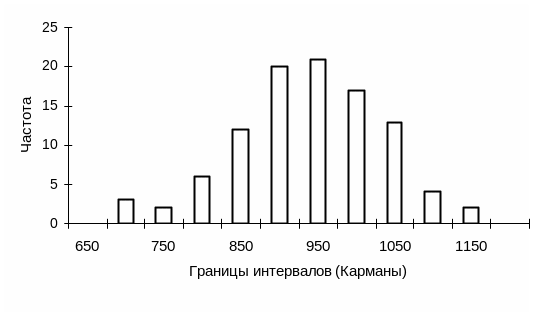
Рис. 2.5.1. Гистограмма, построенная по данным табл. 2.2.1.
Расчет статистических характеристик и построение гистограммы в пакете STATISTICA. В версии пакета 6.0 расчет статистических характеристик и построение гистограммы определяются процедурой состоящей из следующих шагов.
Шаг 1. Ввести или импортировать (например, из Excel) исходные в рабочую книгу (Workbook) системы STATISTICA.
Шаг 2. Выделить столбец с введенными или импортированными данными, для которого необходимо рассчитать статистические характеристики и построить гисторамму. При необходимости можно изменить название столбца.
Шаг 3. Щелкнуть по кнопке Start menu …, расположенной в левом нижнем углу окна приложения и в появившемся меню выбрать Statistics ® Basic Statistics and Tables ® Descriptive Statistics
Шаг 4. Требуемые статистические характеристики (описательные статистики) задаются в окне Descriptive Statistics на вкладке Advanced.
Шаг 5. Для построения таблицы с абсолютными и относительными частотами попадания данных в автоматически выбранный интервал и гистограммы используется кнопки Frequency table, Histograms на вкладку Quick окна Descriptive Statistics.
Вкладка Advanced окна Descriptive Statistics.
Вкладка Quick окна Descriptive Statistics
Пример 2.4.2. Для примера выполним начальную статистическую обработку для исходных данных с таблицы 2.2.1. Исходные данные импортированы из таблицы Excel предыдущего примера. Статистические характеристики, таблица частот и гистограмма, полученные по технологии начальной статистической обработки пакета STATISTICA. приведены ниже.
