4.8. Контрольные вопросы и задания

4.8.1.Вопросы

1. Корреляционный анализ и его задачи.

2. Общую схема взаимосвязей параметров и факторов в стохастической системе.

3. Корреляционные поля, их назначение.

4. Выборочный коэффициент корреляции и его вычисление.

5. Свойства коэффициента корреляции.

6. Корреляционная матрица.

7. Проверки статистической гипотезы о значимости коэффициента корреляции.

8. Корреляционное отношение и его свойства.

9. Вычисление корреляционного отношения.

10. Частные коэффициенты корреляции.

11. Ранговая корреляция, ранговый коэффициент корреляции Спирмэна.

12. Коэффициент конкордации Кендалла.

4.8.2. Задания

Задание 1. С помощью технологии корреляционного анализа статистического пакета statistica построить корреляционные поля для переменных:

1. у ↔ x₁;

2. x₂ ↔ x₅;

3. x₃ ↔ x₅.

из примера 4.7.2.

Задание 2. Описать технологию корреляционного анализа с помощью пакета SPSS. Как пример исследовать наличие и силу корреляционной связи между выборками, приведенными в таблице 3.5.1 и 3.5.2 задания 1 (п. 3.5.2).

Задание 3. Описать возможности модуля Product-Moment and Partial Correlations - Quick, вызываемого из стартовой панели командой Statistics ® Basic Statistics and Tables ® Correlation matrices.

Задание 4. Описать возможности вкладки Prob. & Scatterplots Tab модуля Descriptive Statistics.

5. Регрессионный анализ

5.1. Основные положения

Регрессионный анализ дает более полную информацию о связи результирующей случайной величины (выходной переменной) с входными переменными, которые обычно называют в регрессионном анализе факторами[1,4,5,6,9]. В корреляционном анализе связь между случайными величинами описывается числами (коэффициентом корреляции, корреляционным отношением), а в регрессионном анализе описывается с помощью функций - уравнений регрессии. Уравнение регрессии может быть записано в виде:

(5.1.1)

где - оценка условного математического ожидания случайной величины y при условии, что многомерная случайная величина, определяющая совокупность входных переменных, принимает значения .

Пусть в результате наблюдений выходная переменная принимает в каждом i-ом наблюдении определенные значения y_i, при соответствующем наборе значений входных переменных x₁,x₂...x_к. Если провести серию из n наблюдений, то результаты наблюдений можно представить в следующем виде:

№ наблюдение	Выходная переменная	Входные переменные
1-ое наблюдение	y1	x11, x12,...,x1k
2-ое наблюдение	y2	x21, x22,...,x2k
3-е наблюдение	y3	x31, x32,...,x3k
.................................	....................	........................
n-ое наблюдение	yn	xn1, xn2,...,xnk

Зависимость случайной величины y от независимых переменных x₁,x₂,...,x_k, если учитывать только линейные эффекты, т.е. пренебречь совместным влиянием факторов x_ij, x_ii, отражается уравнением множественной регрессии:

y=b₀+b₁x₁+b₂x₂+...+b_kx_k; (5.1.2)

Для получения оценок коэффициентов b₀,b₁,b₂,...,b_k уравнения регрессии (5.1.2) используется метод наименьших квадратов [9]. Оценки b_S, s=0,k получаются из решения систем уравнений, образованных приравниванием нулю частных производных по b_S формы

(5.1.3)

В результате решения такой системы уравнений для оценки параметра b₀ получено:

(5.1.4)

Параметр b₀ называется свободным членом и он определяет пересечение ординаты при равных нулю независимых переменных. Выражение для оценок определяется следующим образом.

Введем обозначения:

(5.1.5 а).

(5.1.5 б).

Элементы l_rs образуют матрицу, определитель которой обозначим Z и, если обозначить Z_s определитель матрицы, получающейся заменой S столбца на , то:

, (5.1.6).

На основе элементов матрицы рассчитываются парные коэффициенты корреляции r_is между независимыми переменными x_s, i,s =1,k и коэффициенты корреляции r_i0 между зависимой переменной y и независимыми переменными. Элементы r_is составляют корреляционную матрицу. Исходя из парных коэффициентов корреляции, можно рассчитать коэффициент множественной корреляции

(5.1.7).

где

r_ij^-1-элементы матрицы, обратной к корреляционной матрице.

Оценка значимости коэффициентов регрессии производится с помощью t-критерия. Для получения вычисленных значений t-критерия используется формула:

(5.1.8).

Среднеквадратичное отклонение коэффициентов регрессии равно:

(5.1.9).

где

e_i-отклонение фактических значений y от рассчитанных по уравнению регрессии.

Предпосылки. Предполагается, что “зависимая” случайная величина y подчинена нормальному закону распределения с постоянной дисперсией.

Рекомендуется перед проведением регрессионного анализа:

• оценить влияние неконтролируемых и контролируемых неучитываемых переменных на распределение “зависимой” переменной у;

• исключить из анализа линейно зависимые факторы;

• оценить временную стабильность распределения у, для чего проверить гипотезы об однородности среднеарифметических и дисперсии у, рассчитанных по результатам выборок, взятых в разное время.

Также, анализ полученного уравнения регрессии затрудняет разнобой в единицах измерения разных факторов (градусы, тонны, километры, ангстремы и т.п.). Для того, чтобы по виду уравнения можно было составить представление о степени влияния каждого фактора на выходную переменную, необходимо перейти к безразмерным величинам. Вместо случайных величин берут центрированные, нормированные случайные величины

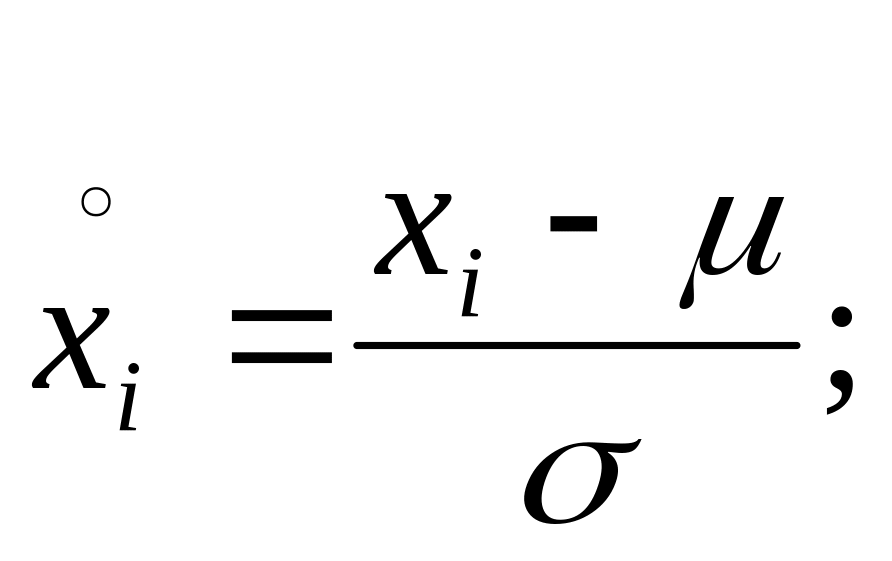(5.1.10).

Для нормированных величин уравнение регрессии (5.1.2) примет вид

(5.1.11)

Приведенные (стандартизованные, нормированные) коэффициенты β_i характеризуют реальный вклад каждого из факторов в вариацию выходной переменной y. Чем больше абсолютная величина β_i, тем этот вклад больше.