
Теоретическая Часть Типовика № 2 «исследование Функций» По Высшой Математике (Старинец В. В.)
.docxТиповой индивидуальный расчет №2
«Исследование функций»
3.1. Теоретические вопросы
1. Сформулируйте теоремы Ролля, Лагранжа и Коши.
Теорема Ролля.
Если
функция y=f(x)
непрерывна на отрезке [a,b],
дифференцируема во всех его внутренних
точках, а на концах отрезка х=а, х=b
обращается в ноль, то существует, по
крайней мере, одна точка с
 (a,
b,)
, в которой f
`(c)=0
(a,
b,)
, в которой f
`(c)=0
Теорема Лагранжа.
Если функция y=f(x) непрерывна на отрезке [a, b], дифференцируема во всех его внутренних точках, то найдется такая точка с , что выполняется f(b) - f(a) = f `(c) ( b - a ) .
Теорема Коши.
Если функция f(x) и (x) непрерывны на отрезке [a, b] и дифференцируемы внутри отрезка, причем `(x) ≠ 0 , тогда внутри отрезка [a, b] найдется точка с , такая что
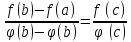 .
.
2. Какая связь между возрастанием и убыванием функции и знаком ее производной?
Если функция y=f(x) имеющая на отрезке [a,b] возрастание (убывание), то ее производная на отрезке [a,b] отрицательная (положительная).
3. Какая точка называется точкой локального экстремума функции?
Точка
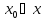 называется точкой локального
максимума(минимума) функции f(x)
, если существует окрестность
называется точкой локального
максимума(минимума) функции f(x)
, если существует окрестность
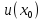 точки
точки
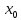 в множестве Х , такая что
в множестве Х , такая что
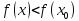 (
(
 ) в любой точке
) в любой точке
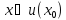 и
и
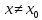 .
.
4. Как расположена касательная к графику функции в точке экстремума?
В точке экстремума касательная к графику горизонтальна.
5. Сформулировать достаточные условия экстремума функции.
Для
того, что бы точка
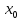 , была точкой экстремума функции f(x),
определенной в окрестности точки
, была точкой экстремума функции f(x),
определенной в окрестности точки
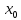 , необходимо выполнении одного из двух
условий – либо функция не имеет
производной в
, необходимо выполнении одного из двух
условий – либо функция не имеет
производной в
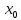 , либо эта производная существует и
равна нулю.
, либо эта производная существует и
равна нулю.
6. Дать определение выпуклости и вогнутости графика и его точек перегиба.
Кривая
называется выпуклой вверх на интервале
(a;b)
, если она расположена ниже касательной,
проведенной в любой её точке. Кривая
называется выпуклой вниз на интервале
(c;d)
, если она расположена выше любой ее
касательной на этом интервале. Пусть
функция y=f(x)
определена и непрерывна на некотором
интервале, содержащем точку
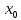 , имеет на этом интервале вторую
производную, за исключением, быть может,
самой точки
, имеет на этом интервале вторую
производную, за исключением, быть может,
самой точки
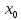 , тогда если
, тогда если
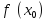 или
или
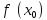 не существует и при переходе аргумента
через
не существует и при переходе аргумента
через
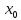 производная
производная
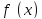 меняет знак, то точка
меняет знак, то точка
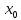 является точкой перегиба кривой
является точкой перегиба кривой
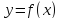 .
.
7. Какова связь между выпуклостью и вогнутостью графика и знаком ее второй производной?
Если
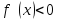 во всех точках интервала (a;b)
, то кривая
во всех точках интервала (a;b)
, то кривая
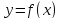 выпукла вверх. Если
выпукла вверх. Если
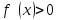 во всех точках интервала (c;d)
, то кривая
во всех точках интервала (c;d)
, то кривая
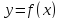 выпукла вниз.
выпукла вниз.
8. Сформулируйте достаточные условия существования точек перегиба.
Если вторая производная функции при переходе через точку меняет знак, то функция в этой точке имеет перегиб, т.е. функция в этой точке меняет вогнутость.
Если в данной точке производная (n-1)-го порядка обращается в ноль, а производная n-го порядка (не четная) не обращается в ноль, то в этой точке функция имеет перегиб.
9. Что называется асимптотой кривой? Что можно сказать о функции, если она имеет горизонтальную (вертикальную) асимптоту?
Прямая называется асимптотой неограниченной кривой, если расстояние от переменной точки кривой до этой прямой стремится к нулю при удалении точки в бесконечность.
Асимптоты, параллельные оси ординат, называют вертикальными, а непараллельные оси ординат – наклонными. Частным случаем наклонной асимптоты является горизонтальная, т.е. параллельная оси абсцисс.
10. Необходимое и достаточное условие существования наклонной асимптоты.
Прямая
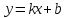 является наклонной асимптотой при
является наклонной асимптотой при
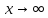 , если
, если
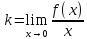 ,
,
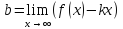 при условии того, что оба указанных
предела существуют.
при условии того, что оба указанных
предела существуют.
Функция имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту, или одну наклонную и одну горизонтальную, или две наклонных, или две горизонтальных, либо же вовсе не имеет асимптот.
