Глава 2 Примеры решения задач.

Задача 1. В заданной плоскости построить через точку А горизонталь, чeрез точку В-фронталь.

Ход решения

Горизонталью плоскости называется прямая, лежащая в данной плоскости, и параллельная горизонтальной плоскости проекций (рис.31)

Рис.31

Фронтальная проекция горизонтали h₂ всегда параллельна оси х_12.

Фронталью плоскости называется прямая, лежащая в данной плоскости и параллельная фронтальной плоскости проекций (рис.32).В плоскости АВСД построили фронталь f через точку А, а затем ей параллельно через точку В провели искомую f*.

Рис.32

Горизонтальная проекция фронтали f₁ всегда параллельна оси х_12.

Задача 2. Построить фронтальную проекцию треугольника АВС, принадлежащего плоскости (рис. 33).

Рис.33

Точка принадлежит плоскости, если она лежит на прямой принадлежащей этой плоскости. В качестве прямых, принадлежащих плоскости, удобно воспользоваться главными линиями плоскости – горизонталью (h) или фронталью (f).

Ход решения

1. Построим фронтальную проекцию B₂ . Для этого через горизонтальную проекцию B₁ проведем горизонтальную проекцию фронтали параллельно оси х ₁₂ , построим ее фронтальную проекцию параллельно f₂ и отметим на ней фронтальную проекцию B₂.(рис.34).

Рис. 34 Рис.35

2. Аналогично строим фронтальную проекцию C₂.

3. Построим фронтальную проекцию точки А₂. Если горизонтальная проекция точки А₁ принадлежит горизонтальной проекции прямой h₁, то фронтальная проекция А₂ находится на h₂ (рис. 35).

4. Соединим А₂В₂С₂ и получим недостающую фронтальную проекцию треугольника АВС (рис.35).

Задача 3. Построить линию пересечения двух плоских фигур (рис. 36)

Дано: Плоскость α(ΔАВС) частного положения (ΔАВС П₁), плоскость β (ΔMNK) – общего положения .

Рис.36

Две плоскости пересекаются по прямой. Чтобы построить эту прямую, надо найти две общие точки для этих плоскостей.

Ход решения

1. Поскольку ΔАВС является горизонтально-проецирующей плоскостью , линия пересечения плоскостей будет принадлежать горизонтальной проекции ΔАВС. Отметим общие горизонтальные проекции Q₁ и T₁ на пересечении горизонтальных проекций треугольников АВС и MNK (рис.37).

2.Проведем линии проекционной связи и отметим фронтальные проекции Q₂ и T₂ в ΔM₂N₂K₂.

3. Линия пересечения QT определена фронтальной Q ₂T₂ и горизонтальной проекцией Q₁T₁.

4. Определим видимость плоских фигур, т.к. плоскости считаются непрозрачными. Видимость на горизонтальной плоскости проекций определять не надо, т.к. ΔАВС проецируется в прямую линию, следовательно проекция M₁N₁K₁видима. Определим видимость плоских фигур на плоскости проекций П ₂. Для этого рассмотрим конкурирующие точки 1 и 2, лежащие на скрещивающихся прямых ВС и МK. Фронтальные проекции 1₂ и 2₂ совпадают, а горизонтальная проекция 2₁ находится перед горизонтальной проекцией 1₁. Точка 2 видима относительно плоскости проекций П₂. Следовательно сторона B₂C₂ видима, фронтальная проекция ΔА₂В₂С₂ видима на П₂ с той стороны, где находятся точки 1₂ и 2₂. После фронтальной проекции линии пересечения Q₂T₂ становится видимым ΔMNK (рис.37).

Рис. 37

Задача 4. Построить линию пересечения плоскостей (рис.38).

Заданы две плоскости общего положения γ(f∩h) и δ(а∩b).

Рис. 38

Ход решения

1. Проведем вспомогательную плоскость частного положения, например плоскость горизонтального уровня α ׀׀ П₁ (рис.39).

2. Плоскость α пересечет плоскость γ(f∩h) по горизонтали h*.

3. Плоскость α пересечет плоскость δ (а∩b) по прямой 2-3.

4. Прямые h* и 2-3 пересекаются в точке M (M₁ и M₂₎

Рис. 39

5. Для построения второй общей точки проведем еще одну вспомогательную плоскость β ׀׀ П₁ (рис40.).

6. Плоскость β пересечет плоскость γ(f∩h) по горизонтали h'.

7. Плоскость β пересечет плоскость (а∩b) по прямой 5-6.

8. Прямые h' и 5-6 пересекутся в точке N(N₁ и N₂). Соединяем одноименные проекции точек М и N получим проекции линии пересечения (М₁N₁) и (М₂N₂).

Рис. 40

Задача 5. Построить точку пересечения прямой l с плоскостью . Определить видимость прямой l (только в случае задания плоскости плоской фигурой).

Пример 1. Плоскость β задана двумя пересекающимися прямыми h и f (рис.41).

Рис.41 Рис. 42 Рис.43

Ход решения

1. Для построения точки пересечения прямой l с плоскостью необходимо через прямую провести вспомогательную плоскость частного положения, например фронтально-проецирующую α П₂, l₂≡α₂(рис.42 ).

2. Строим линию пересечения 1-2 заданной плоскости β и вспомогательной плоскости α (рис. 43)

3. Определяем точку пересечения К заданной прямой l с линией пересечения 1-2.

4. Видимость прямой l не определяем.

Пример 2. Плоскость задана ΔАВС (рис. 44).

Рис. 44

Ход решения

1. Через прямую l проводим вспомогательную плоскость частного положения, например, горизонтально-проецирующую α П_1, l₁ ≡α₁ (рис. 45).

2. Строим линию пересечения MN заданной и вспомогательной плоскостей. М₁=А₁С₁ ∩ α_1, М₂ А₂С₂ и N₁=В₁С₁∩ α _1,N₂ В₂С₂ (рис. 46).

Рис. 45 Рис.46

3. Строим точку пересечения К заданной прямой l с линией пересечения МN. К₂= М₂N₂∩l₂. К₁ находится на М ₁N₁.

4. Определяем видимость прямой относительно ΔАВС с помощью конкурирующих точек.

Определяем видимость на плоскости П₂ .Отметим фронтальную проекцию 1₂, совпадающую с 2_2. Горизонтальную проекцию 2₁ отметим на А₁С₁, а 1₁ на l₁. Горизонтальная проекция 1₁ лежит перед 2₁, следовательно, точка 1 видима на П₂. Точка 1 лежит на прямой l, она видима на П₂, следовательно фронтальная проекция l₂ до К₂ видима, в точке К₂ видимость меняется на невидимую .

Определим видимость прямой l на П₁. Отметим горизонтальную проекцию 3₁ совпадающую с горизонтальной проекцией М₁. М₂ А₂С₂ уже отмечена, 3₂ l₂. Фронтальная проекция М₂ лежит выше фронтальной проекции 3₂, следовательно, точка М видима на П₁ .Плоскость закрывает прямую l до К ₁, горизонтальная проекция l ₁ невидима. В горизонтальной проекции К ₁ видимость меняется на видимую . За границами ΔАВС прямая l видима.

Задача 6. Построить линию пересечения плоскости общего положения с заданной поверхностью.

Пример 1. Трехгранная призма (рис.47).

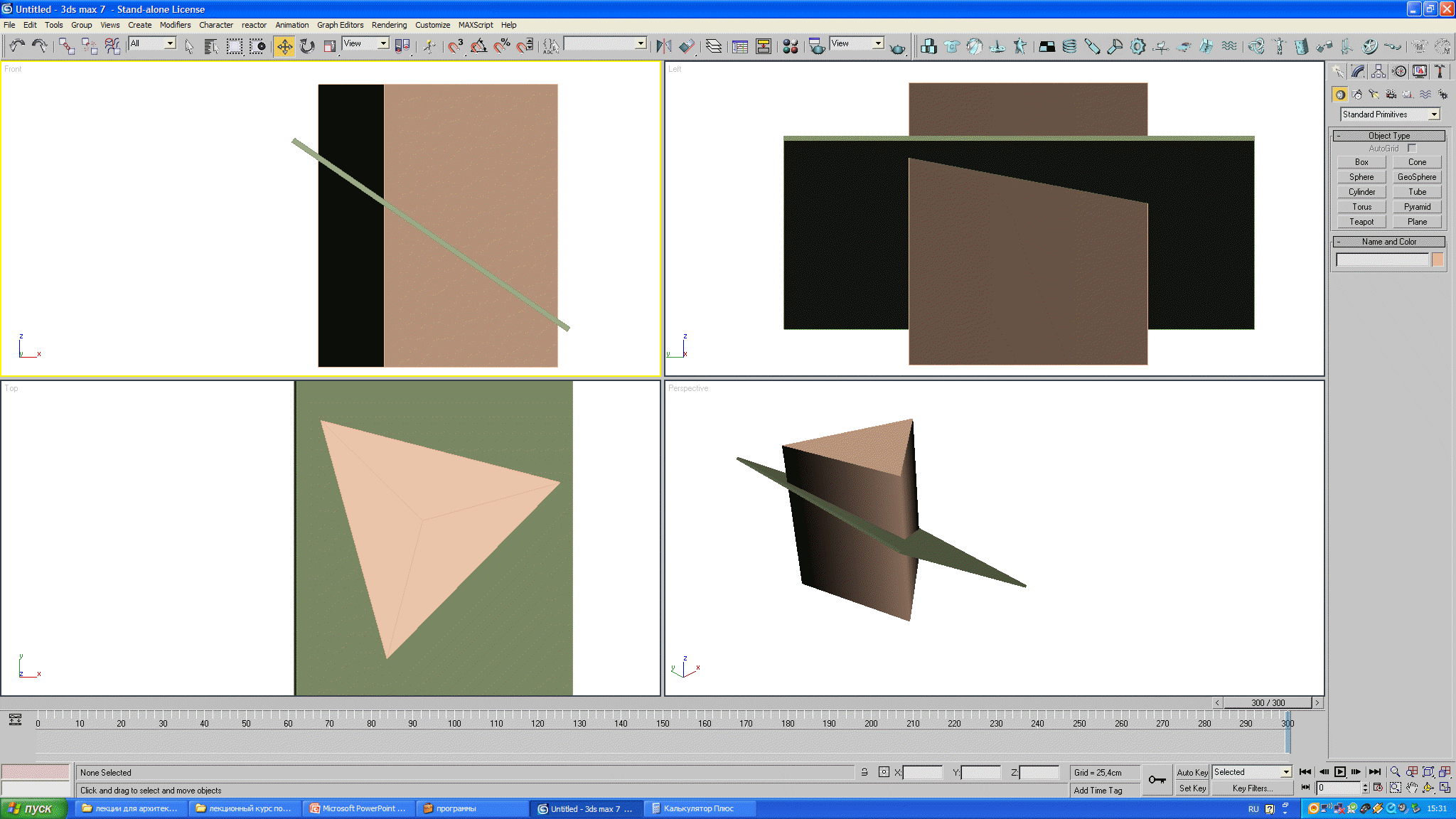
Рис.47