
- •Лекция 1. «Определители».
- •Практическое занятие №1.Определители. Вопросы для самопроверки.
- •Примеры решений задач.
- •Задания для аудиторной и домашней работы.
- •Ответы:
- •Задания для индивидуальной самостоятельной работы №1.
- •Практическое занятие №2.
- •3. Найти обратную матрицу для матрицы
- •Задания для аудиторной и домашней работы:
- •Лекция №3. Системы линейных уравнений (слу) и их решение.
- •Задачи для аудиторной и домашней работы.
- •Задания для индивидуальной самостоятельной работы.
- •Лекция 4. «Основы векторной алгебры».
- •Практическое занятие №4. Векторы. Линейные операции над векторами. Скалярное произведение векторов.
- •Задания для индивидуальной самостоятельной работы №4.
- •Лекция №6 Введение в математический анализ.
- •Лекция №8. Дифференциал. Теоремы о среднем. Правило Лопиталя. Формула Тейлора.
- •Практическое занятие №8. Дифференциал. Производные и дифференциалы высших порядков. Теоремы о среднем. Правило Лопиталя.
- •1. Найти дифференциал следующих функций:
- •2. Найти производные и дифференциал второго порядка функций:
- •3. Теоремы о среднем:
- •4. Правило Лопиталя:
- •5. Формула Тейлора и Маклорена:
- •2. Исследовать на экстремум функции:
- •4. Найти промежутки выпуклости и выгнутости графика функции
Практическое занятие №4. Векторы. Линейные операции над векторами. Скалярное произведение векторов.
Вопросы для самопроверки.
Что называется геометрическим вектором?
Что называется длиной(модулем) вектора?
Что называется нулевым вектором?
Какой вектор называется единичным вектором?
Какие векторы называются противоположными?
Какие векторы называются коллинеарными?
Какие векторы называются компланарными?
Какие векторы называются равными?
Дайте определение суммы двух векторов.
Дайте определение разности двух векторов.
Дайте определение произведения вектора на число.
Напишите признак коллинеарности двух ненулевых векторов.
Напишите признак компланарности трех ненулевых векторов.
Дайте определение угла между неколлинеарными векторами.
Дайте определение проекции вектора на ось.
Сформулируйте основные свойства проекции на ось.
Как определяется прямоугольная система координат на плоскости( в пространстве)?
Как определяются координаты вектора в прямоугольной системе координат? Напишите координатную форму геометрического вектора.
По какой формуле вычисляется длина вектора?
По каким формулам вычисляются направляющие косинусы вектора?
По какой формуле связаны направляющие косинусы вектора?
Дайте определение радиус-вектора точки определение координат точки.
Как записываются в координатах условия равенства, коллинеарности и компланарности векторов?
Как записываются в координатах линейные операции над векторами?
Как вычисляются координаты вектора, заданные двумя точками?
Как вычисляется расстояние между точками, через их координаты?
Как вычисляется координаты точки, делящий отрезок в данном отношении?
Дайте определение скалярного произведения векторов.
55
Сформулируйте свойства скалярного произведения.
Какие задачи можно решить с помощью скалярного произведения?
Примеры решения задач.
При каких значениях х векторы х
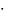
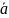 и (
и (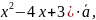
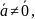 противоположно направлены?
противоположно направлены?
Решение.
Эти векторы противоположно направлены,
если множители х и
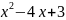 имеют разные знаки, т.е. их производные
отрицательны.
имеют разные знаки, т.е. их производные
отрицательны.

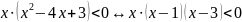 Отмечая
корни
Отмечая
корни
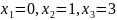 на
числовой оси, в каждой промежутке
определяем знак выражения
на
числовой оси, в каждой промежутке
определяем знак выражения
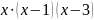 и
составляем ответ. - + -
+
и
составляем ответ. - + -
+
0 1 3
Ответ:
х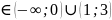
В прямоугольнике АВС:

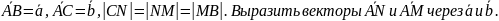
Решение.
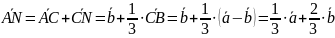 .
.
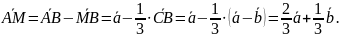
Ответ:
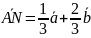 ;
;
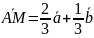 .
.
Векторы образуют угол
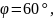 причем
причем
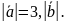


C
D
Определить
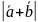 и
и
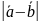 .
.
B
A

 .
На векторах
построим
.
На векторах
построим
параллелограмму ABCD:
 =
=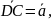
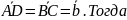
 +
+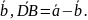 Далее,
применяя теорему косинусов треугольникам
Далее,
применяя теорему косинусов треугольникам
56
ABC
и ABD
получаем:
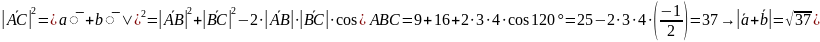 .
.
 =
=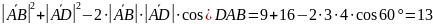
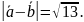
Ответ:
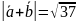 ;
;
При каких значениях
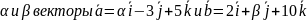 коллинеарны?
коллинеарны?
Решение.
Из коллинеарности векторов следует,
что их соответствующие координаты
пропорциональны:
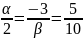 .
Отсюда :
.
Отсюда :
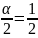 и
и
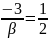 .
Итак,
.
Итак,
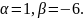
Ответ:
Разложить вектор
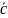 =(4;3;7)
по векторам
=(4;3;7)
по векторам
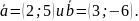
Решение.
Требуется представить
в виде
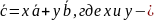
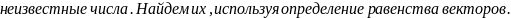
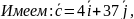
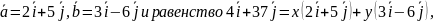 т.е.
т.е.
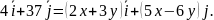
Отсюда
следует, что
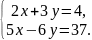
Решая
СЛУ,
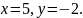 Следовательно,
Следовательно,
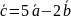 .
.
Ответ: .
Найти орт вектор вектора

Решение.
Из равенства
 находим, что
находим, что
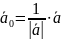 .
Далее
.
Далее
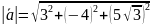 =
=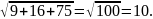 Значит,
Значит,
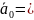 (
(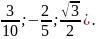
57
Ответ: (
Вектор
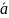 составляет с осью Ox
угол 60
составляет с осью Ox
угол 60 ,
а с осью Oy угол 45
,
его модуль
,
а с осью Oy угол 45
,
его модуль
 ,
если его аппликата отрицательна.
,
если его аппликата отрицательна.
Решение.
Пусть x, y, z- координаты вектора
,
т.е.
=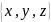 .
Координаты вектора
найдем
.
Координаты вектора
найдем
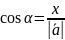 ,
,
 ,
,
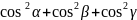 =1,
=1,
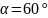 ,
,
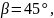 то
то
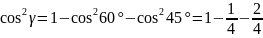 =
=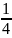 .
Отсюда находим, что
.
Отсюда находим, что
 Условию
задачи удовлетворяет
Условию
задачи удовлетворяет
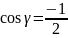 ,
т.к. z<0.
Имеем
,
т.к. z<0.
Имеем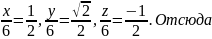 x=3,
y=3
x=3,
y=3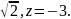
Ответ:

Дан вектор =(2;-1;20, Найти вектор , параллельный вектору и противоположного с ним направления, если

Решение.
По условию задачи
 Тогда
Тогда
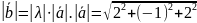 =
=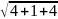 =3.
=3.
Итак,
3 =15,
=15,
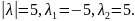 Условию
задачи удовлетворяет
Условию
задачи удовлетворяет
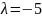 .
Следовательно,
.
Следовательно,

Ответ:
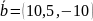 .
.
Известно, что =3, =4,
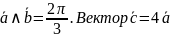 -3
.
Определить длину вектора
.
-3
.
Определить длину вектора
.
Решение.
Используем формулу
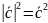 .
Далее,
.
Далее,
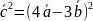 =16
=16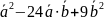 =16
=16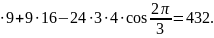
Отсюда
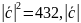 =
=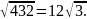
Ответ:
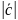 =
=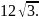
Даны векторы
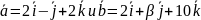 .
Вычислить
.
Вычислить
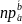 и
.
и
.
Решение.
Используем формулу
= .
Вычислим скалярное произведение векторов
.
Вычислим скалярное произведение векторов
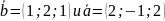 по формуле
по формуле
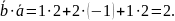
58
Вычислим
модуль вектора
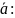 =
=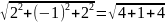 =3.
=3.
Итак,
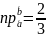 .
.
Аналогично,
=
=
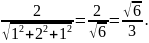
Ответ:
=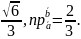
Найти угол между диагоналями параллелограмма, построенный на векторах =
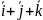 и
и
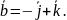
Решение.
Одному из диагоналей соответствует
вектор
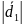 =
=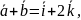 другому-
вектор
другому-
вектор
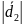 =
=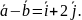 Косинус
угла между векторами
Косинус
угла между векторами
 находим по формуле
находим по формуле
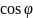 =
=
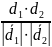 .
=
.
= =
=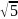 ;
;
 =1
1+2
=1
1+2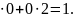
Итак,
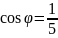 и
и
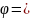 arccos
arccos
Ответ: arccos
Найти угол между векторами
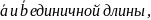 если
известно, что векторы
если
известно, что векторы
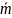 =
=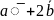 и
и
 взаимно
перпендикулярны.
взаимно
перпендикулярны.
Решение.
Векторы
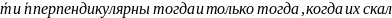 ярное
произведение равно нулю:
ярное
произведение равно нулю:
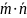 =0
=0
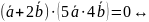 5
5 -4
-4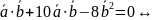 5
+6
5
+6 =0.
По условию
=0.
По условию
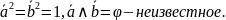 Тогда 5
Тогда 5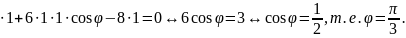
Ответ:

59
Задачи для аудиторной и домашней работы.
По данным векторам построить каждый из следующих векторов: 1) 3

2)
2 3)
3)
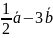 .
.
2.
В треугольнике АВС вектор и
=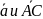 =
.
Построить каждый из следующих векторов:
1)
=
.
Построить каждый из следующих векторов:
1)
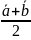 ;
2)
;
2)
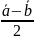 ;
3) -
;
4)
;
3) -
;
4)
 .
.
3.
В треугольнике АВС вектор и
=
=
.
Найти вектор
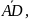 идущих
по биссектрисе угла ВАС.
идущих
по биссектрисе угла ВАС.
4.
В треугольнике АВС проведены медианы
АD,
BE, и CF. Найти сумму векторов
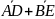 +
+
5.
В параллелепипеде
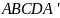 B'C'D'
заданы векторы
=
B'C'D'
заданы векторы
=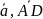 =
=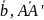 =
= .
Построить каждый из следующих векторов:
1)
.
Построить каждый из следующих векторов:
1)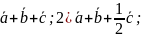 3)
3)
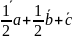 ;
4)
;
4)
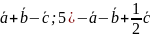 .
.
6. Проверить, что 4 точки А(-1;5;-10), В(1;2;-1), С(-1;1;-3), D(3;-5;3) служат вершинами трапеции.
7.
Даны точки А (-1;5;-10), В (5;-7;8), С (2;2;-7) и D
(5;-4;2). Проверить, что векторы
и
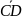 коллинеарны; установить, какой из них
длиннее другого и во сколько раз, как
они направлены- в одну сторону или в
противоположные стороны.
коллинеарны; установить, какой из них
длиннее другого и во сколько раз, как
они направлены- в одну сторону или в
противоположные стороны.
8.
Определите модули суммы разности
векторов
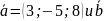 =(-1;1;-4).
=(-1;1;-4).
9.
Определите, при каких значениях
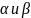 векторы
векторы
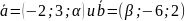 коллинеарны.
коллинеарны.
10.
Вектор
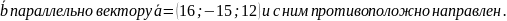 Найти координаты вектора
,
если
=75.
Найти координаты вектора
,
если
=75.
11.
Найти орт вектора

60
12.
Даны
=13,
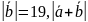 =24.
Вычислить
.
=24.
Вычислить
.
13.
Даны
=11,

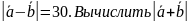 .
.
14.
Векторы
и
взаимно перпендикулярны, причем
=3
и
 .
.
15.
Векторы
и
образуют угол
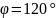 ,
причем
=3
и
,
причем
=3
и
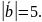 Определить
Определить
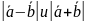 .
.
16. Определите, принадлежат ли точки А(1;-1;2), В(2;0;3), С(4;1;-1), D(3;1;4) на одной плоскости.
17.
Как должен быть связаны векторы
и
,
чтобы выполнялись соотношения: 1)
=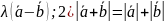 ;
3)
;
3)
 ;
4)
;
4)
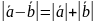 ;
5)
;
5)
 ?
?
18.
На плоскости даны два вектора
=(2;-3)
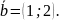 Найти разложение вектора
=(9;4)
по базису
,
.
Найти разложение вектора
=(9;4)
по базису
,
.
19.
На плоскости даны векторы
=(3;-2),
 базису
,
.
базису
,
.
20.
В пространстве даны векторы
=(3;-2;1),
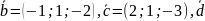 =(11;-6;;5).
Найти разложение вектора
=(11;-6;;5).
Найти разложение вектора
 ,
.
,
.
21.
В пространстве даны векторы
=(2;1;0),
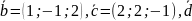 =(3;7;-1).
Найти разложение вектора
,
.
=(3;7;-1).
Найти разложение вектора
,
.
22.
Векторы
и
образуют угол
 +2
+2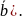
23.
Векторы
и
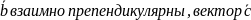 образует
с ними угол углы, равные
образует
с ними угол углы, равные
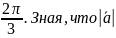 =3
и
=3
и
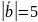 ,
=8,
вычислить
,
=8,
вычислить
 2
2 .
.
24.
Даны векторы
=(4;-2;-4),
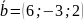 .
Вычислить: а) (
.
Вычислить: а) (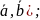 б)
б)
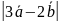 ;
в)
;
в)
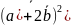 ;
г)
;
г)
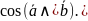
61
25.
Даны векторы
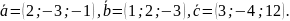 Вычислить: а)
Вычислить: а)
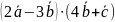 ;
б)
;
б)
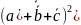 ;
в)
;
в) ).
).
26.
Определить, при каком значении
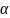 векторы
векторы
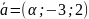 и
и
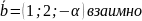 перпендикулярны.
перпендикулярны.
27.
Даны векторы
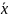 ,
коллинеарный вектору
,
коллинеарный вектору
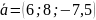 ,
образует острый угол с осью Оz. Зная, что
,
образует острый угол с осью Оz. Зная, что
 =50,
найти его координаты.
=50,
найти его координаты.
28.
Даны векторы
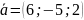 ,
,
 ,
,
 .
Найти вектор
,
если
.
Найти вектор
,
если
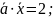
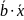 =14;
=14;
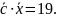
29.
Найти вектор
,
зная, что он перпендикулярен к векторам
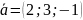 и
и
 и удовлетворяет условию
и удовлетворяет условию
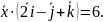
30.
Даны точки А(1;-1;1), В(2;2;-1), С(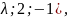 D(3;5;-3
D(3;5;-3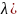 .
При каких значениях
векторы
,
.
При каких значениях
векторы
,
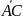 ,
,
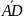 компланарны?
компланарны?
Ответы:
3.
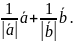 4.
4.
 6.
6.
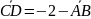 ,
не //
.
7.
=2
,
не //
.
7.
=2 ,
=2
,
=2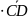 ,
,
 8.
=6;
8.
=6;
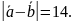 9.
9.
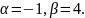 10.
10.
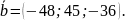 11.
(
11.
(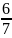 ;
;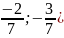 .
12.
22 13.
20 14.
5 15.
.
12.
22 13.
20 14.
5 15.
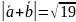 ,
,
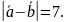 16.
Да 17.
16.
Да 17.
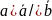 ;
б)
;
б)
 ;
в)
;
в)
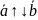 ;
г)
;
г)
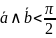 ;
д)
;
д)
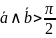 .
18.
.
18.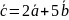 .
19.
.
19.
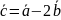 .
20.
.
20.
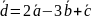 .
21.
.
21.
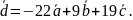 22.
-13. 23.
-668. 24.
а)22; б) 16; в)320; г)
22.
-13. 23.
-668. 24.
а)22; б) 16; в)320; г)
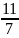 25.
а)-41; б) 125; в)
25.
а)-41; б) 125; в)
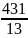 .
26.
-6. 27.
(-24;-32;30) 28.
(1;2;3) 29.
(3;-3;-3). 30.
.
26.
-6. 27.
(-24;-32;30) 28.
(1;2;3) 29.
(3;-3;-3). 30.
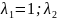 =-2.
=-2.
62
