
- •Лекция 1. «Определители».
- •Практическое занятие №1.Определители. Вопросы для самопроверки.
- •Примеры решений задач.
- •Задания для аудиторной и домашней работы.
- •Ответы:
- •Задания для индивидуальной самостоятельной работы №1.
- •Практическое занятие №2.
- •3. Найти обратную матрицу для матрицы
- •Задания для аудиторной и домашней работы:
- •Лекция №3. Системы линейных уравнений (слу) и их решение.
- •Задачи для аудиторной и домашней работы.
- •Задания для индивидуальной самостоятельной работы.
- •Лекция 4. «Основы векторной алгебры».
- •Практическое занятие №4. Векторы. Линейные операции над векторами. Скалярное произведение векторов.
- •Задания для индивидуальной самостоятельной работы №4.
- •Лекция №6 Введение в математический анализ.
- •Лекция №8. Дифференциал. Теоремы о среднем. Правило Лопиталя. Формула Тейлора.
- •Практическое занятие №8. Дифференциал. Производные и дифференциалы высших порядков. Теоремы о среднем. Правило Лопиталя.
- •1. Найти дифференциал следующих функций:
- •2. Найти производные и дифференциал второго порядка функций:
- •3. Теоремы о среднем:
- •4. Правило Лопиталя:
- •5. Формула Тейлора и Маклорена:
- •2. Исследовать на экстремум функции:
- •4. Найти промежутки выпуклости и выгнутости графика функции
Ответы:
1. а)
22; б) 5; в) 3; г) 1; д) 0; е)
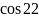 ;
ж) 4ab;
з) 2.
;
ж) 4ab;
з) 2.
2. а) 0; б) 236; в) 120; г) –48; д) –72; е) 42; ж) –2; з) 2.
3. а)
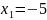 ,
,
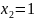 ;
б)
;
б)
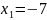 ,
;
в)
,
;
в)
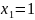 ,
,
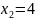 ;
г)
,
;
г)
,
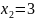 ;
д) 3; е) –4;
ж) –6;
з) 42.
;
д) 3; е) –4;
ж) –6;
з) 42.
4. а)
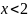 ;
б)
;
б)
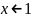 ;
в)
;
в)
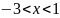 ;
г)
;
г)
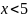 ;
д)
;
д)
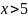 ;
е)
;
ж)
;
е)
;
ж)
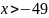 ;
з)
;
з)
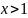 .
.
5. а) 0; б) 472; в) –36; г) –192; д) –74; е) 43; ж) –13; з) 15.
Задания для индивидуальной самостоятельной работы №1.
В каждом задании N – номер вашего варианта.
1. Вычислить определители второго порядка.
а)
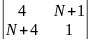 ;
б)
;
б)
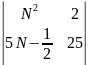 .
.
2. Вычислить определители третьего порядка.
а)
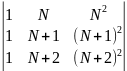 ;
б)
;
б)
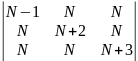 .
.
3. Найти
сумму и произведение корней уравнения
 .
.
18
Лекция №2. Матрицы.
1. Понятие матрицы. Частные виды матриц. Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц. 2. Действия над матрицами и их свойства. Линейная комбинация матриц. 3. Вырожденные и невырожденные матрицы. Понятие обратной матрицы. Теорема о существовании и единственности обратной матрицы. 4. Понятие ранга матрицы.
2.1 Матрицы, впервые появившиеся в середине XIX века в работах английских математиков У. Гамильтона (1805-1865) и А. Кэли (1821-1894), в настоящее время в прикладной математике используются весьма широко, они значительно упрощают рассмотрение сложных систем уравнений.
О. Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов:
А=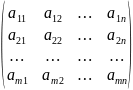 .
(1)
.
(1)
Матрицу А размера m×n
обозначают так:
 .
Числа, составляющие матрицу, называются
её элементами. Элемент матрицы,
стоящий на пересечении строки с номером
i ( номера считываются
сверху вниз) и столбца с номером j
(номера считаются слева направо),
обозначаются
.
При m=n
прямоугольная матрица называется
квадратной матрицей n-ого
порядка
.
Числа, составляющие матрицу, называются
её элементами. Элемент матрицы,
стоящий на пересечении строки с номером
i ( номера считываются
сверху вниз) и столбца с номером j
(номера считаются слева направо),
обозначаются
.
При m=n
прямоугольная матрица называется
квадратной матрицей n-ого
порядка
 .
Главной диагональю квадратной
матрицы называется совокупность
элементов
,
,
… ,
.
Главной диагональю квадратной
матрицы называется совокупность
элементов
,
,
… ,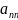 .
Квадратная матрица называется
диагональной, если все её
элементы, лежащие вне главной диагонали,
равны нулю. Единичной матрицей
E n-го порядка
называется диагональная матрица, у
которой каждый элемент находящийся на
главной диагонали, равен единице.
Например,
.
Квадратная матрица называется
диагональной, если все её
элементы, лежащие вне главной диагонали,
равны нулю. Единичной матрицей
E n-го порядка
называется диагональная матрица, у
которой каждый элемент находящийся на
главной диагонали, равен единице.
Например,
Е=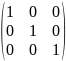 -
единичная матрица 3-го порядка
-
единичная матрица 3-го порядка
Нулевой матрицей называется матрица, все элементы которой равны нулю. Матрицей-столбцом называется матрица, содержащая один столбец. Матрицей-строкой называется матрица, содержащая одну строку. Матрицы А и В одинакового размера называются равными, если каждый элемент матрицы А равен соответствующему элементу матрицы В:
А=В <=>
=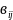 ,
где i=1,2,..,m;
j=1,2,…,n.
(2)
,
где i=1,2,..,m;
j=1,2,…,n.
(2)
О. Элементарными
называются следующие преобразования
матрицы:
1) Перестановка строк(столбцов);
2)
Умножение строки(столбца) на некоторое
число k≠0;
3) Прибавление
к элементам строки(столбца) соответствующих
элементов другой строки(столбца),
умноженных на любое число;
4)
Транспонирование.
О. Две
матрицы А и В одинакового размера
называются эквивалентными, если
существуют невырожденные матрицы P
и Q такие, что A=PBQ.
Обозначение: А В.
В.
19
2.2 О. Суммой матриц А и В размера m×n называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В:
С=А-В,
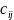 =
= ,
i=1,2,..,m;
j=
1,2,.., n.
(3)
,
i=1,2,..,m;
j=
1,2,.., n.
(3)
О. Разностью матриц А и В размера m×n называется матрица С того же размера, каждый элемент которой равен разности соответствующих элементов матриц А и В:
С=А-В,
=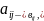 i=1,2,..,m;
j=
1,2,.., n.
(4)
i=1,2,..,m;
j=
1,2,.., n.
(4)
О.
Произведением
матриц А
на число
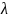 называется матрица В, каждый элемент
которой равен произведению соответствующего
элемента матрицы А на число
:
называется матрица В, каждый элемент
которой равен произведению соответствующего
элемента матрицы А на число
:
В=
*А,
=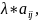 i=1,2,..,m;
j=
1,2,.., n.
(5)
i=1,2,..,m;
j=
1,2,.., n.
(5)
О. Произведением матриц А размера m×k и В размера k×n называется матрица С размера m×n, каждый элемент который равен сумме произведений i-ой строки А на соответствующие элементы j-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В:
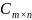 =
=
 *
*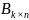 ,
(6)
,
(6)
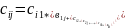 =
=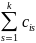 *
* ,
где
i=
,
где
i=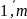 ;
j=
;
j=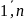 .
.
Получение элемента схематично изображаются так: чтобы найти элемент , нужно «приложить» i-ю строку матрицы А к j-ому столбцу матрицы В, перемножить соответствующие элементы и полученные произведения сложить. Заметим, что умножение матрицы А на матрицу В определено только тогда, когда число столбцов первой матрицы равно числу строк второй.
Пример:
Найти произведение матриц А=
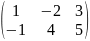 и В=
и В= .
.
Матрица
А имеет размерность 2 3,
а матрица В- 3
2,
т.е число столбцов матрицы А равно числу
строк матрицы В. Значит, А*В=С существует
и размерность матрицы С равна 2
2:
3,
а матрица В- 3
2,
т.е число столбцов матрицы А равно числу
строк матрицы В. Значит, А*В=С существует
и размерность матрицы С равна 2
2:
С= *
=
*
=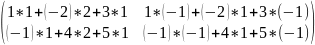 =
=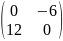
Если произведение А В матриц определено, то нельзя сказать что существует также произведение В А. Если определены оба произведения А В и В А, то в общем случае они не равны.
Пример:
А=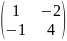 ,
В=
,
В=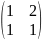 .
.
20
 Тогда
А*В=
Тогда
А*В=
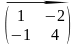 *
=
*
=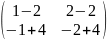 =
=
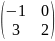
В*А=
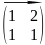 *
=
*
=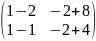 =
=
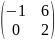 ,
отсюда АВ≠ВА
,
отсюда АВ≠ВА
О.
Транспонированием
матрицы
называется замена строк на её столбцы
с сохранением их порядка.
Если исходная
матрица имеет вид (1),
то транспонированная матрица
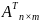 =
= ,
(7)
,
(7)
О.
Возвести
матрицу А в степень n
– это
умножить её на себя n
раз, т.е
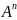 =
=
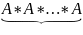 n
раз
Возведение в степень определено
только для квадратных матриц.
Свойства
операций над матрицами:
1.
А+В=В+А ; 8.
(А*В)*С=А*(В*С);
2. (А+В)+С=А+(В+С);
9. (А+В)*С= А*С+ В*С;
3.
(А+В)=
А+
В;
10. А(В+С)= А*В+ А*С;
4.(
n
раз
Возведение в степень определено
только для квадратных матриц.
Свойства
операций над матрицами:
1.
А+В=В+А ; 8.
(А*В)*С=А*(В*С);
2. (А+В)+С=А+(В+С);
9. (А+В)*С= А*С+ В*С;
3.
(А+В)=
А+
В;
10. А(В+С)= А*В+ А*С;
4.(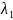 +
+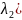 А=
А+
А=
А+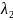 В;
11.
В;
11.
 =
А;
5.
(
А)=
(
*
)А;
12.
=
*
=
А;
5.
(
А)=
(
*
)А;
12.
=
*
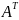 ;
6.
А*В≠В*А 13.
(А+
;
6.
А*В≠В*А 13.
(А+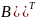 =
+
=
+ 7.Е*А=А*Е=А;
14. (А-
=
7.Е*А=А*Е=А;
14. (А-
=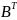 *
.
*
.
Пример:
Найти значение многочлена f(A)
от матрицы А:
f(x)=3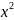 -5х+4,
А=
-5х+4,
А=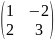 .
Решение:
f(A)=
3
.
Решение:
f(A)=
3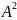 -5A+4E,
где E=
-5A+4E,
где E=
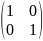 .
1)
=
А*А =
.
1)
=
А*А =
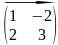 *
=
*
=
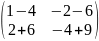 =
=
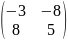
2)
3*
=
3*
=
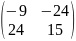 .
.
3)
5*А= 5*
=
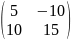 .
.
4)
4Е= 4*
=
 .
.
5)
f(A)
=
-
+
=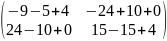 =
=
 .
.
Пусть А и В квадратные матрицы n-го порядка. Тогда их произведение А*В также квадратная матрица n-го порядка.
21
Каждой
квадратной матрице ставится в соответствие
некоторое число, которое называется
определителем
этой матрицы. Оказывается справедливо
свойство: Определитель произведения
двух квадратных матриц равен произведению
определителей этих матриц, т.е
 *
*
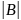 ,
(8)
где
А=
,
В=
,
(8)
где
А=
,
В=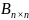 .
.
6.3
О. Матрица
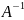 называется обратной
для квадратной матрицы А, если при
перемножении этих матриц получается
единичная, т.е А*
=
*А=Е,
(9)
где
А,
,
Е – матрицы одного порядка.
О. Матрица
А называется невырожденной(неособенной),
если её определитель отличен от нуля
(det
A≠0),
и вырожденной,
если её определитель равен нулю (det
A=0).
называется обратной
для квадратной матрицы А, если при
перемножении этих матриц получается
единичная, т.е А*
=
*А=Е,
(9)
где
А,
,
Е – матрицы одного порядка.
О. Матрица
А называется невырожденной(неособенной),
если её определитель отличен от нуля
(det
A≠0),
и вырожденной,
если её определитель равен нулю (det
A=0).
Теорема.
Обратная матрица
существует( и единственна) тогда и только
тогда, когда исходная матрица А является
невырожденной.
Необходимость
существует => А-невырожденная?
По
условию А*
=Е=>
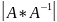 =
=

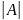 *
*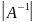 =1=>
≠0,
≠0=>
А и
-
невырожденные матрицы и
=
=1=>
≠0,
≠0=>
А и
-
невырожденные матрицы и
=
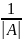 (10)
(10)
Достаточность.
А- невырожденная матрица. Доказать что
существует.
Пусть А=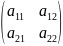 ,
≠0-
невырожденная матрица второго
порядка.
Обозначим
,
≠0-
невырожденная матрица второго
порядка.
Обозначим
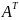 =
=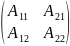 .
Её элементы равны алгебраическим
дополнениям элементов
.
Её элементы равны алгебраическим
дополнениям элементов
 матрицы
матрицы
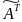 .
Вычислим произведение А и
:
А
*
=
*
=
.
Вычислим произведение А и
:
А
*
=
*
=
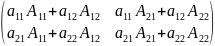 =
= или А *
=
*Е=>
А*(
*
)=
Е (*)
Аналогично,
*
А=
*Е=>
(
*
)*
А = Е. (**)
Сравнивая
неравенства (*)
и
(**) с условием
(9),
установим, что
=
*
,
(10)
т.е
существует и она единственна.
Заметим,
что матрица
называется присоединенной
матрицей к матрице А.
Итак, обратная
матрица для невырожденной матрицы А=
вычисляется по формуле:
=
*
или А *
=
*Е=>
А*(
*
)=
Е (*)
Аналогично,
*
А=
*Е=>
(
*
)*
А = Е. (**)
Сравнивая
неравенства (*)
и
(**) с условием
(9),
установим, что
=
*
,
(10)
т.е
существует и она единственна.
Заметим,
что матрица
называется присоединенной
матрицей к матрице А.
Итак, обратная
матрица для невырожденной матрицы А=
вычисляется по формуле:
=
*
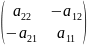 .
(11)
Для
невырожденной матрицы третьего порядка
А=
.
(11)
Для
невырожденной матрицы третьего порядка
А=
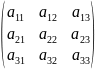 ,
по формуле
=
*
,
по формуле
=
* .
(12)
.
(12)
22
Вычисление
обратной матрицы по формуле (10) называется
методом
присоединенной матрицы.
Пример:
Вычислить матрицу, обратную для А=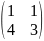 .
1)
=
.
1)
=
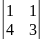 =3-4=
-1
=3-4=
-1 0;
2)
По формуле (11):
=
0;
2)
По формуле (11):
=
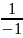 *
* =
=
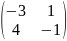 .
.
Свойства
обратных матриц:
1.
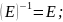 3.
3.
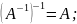 5.
5.
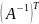 =.
=.
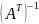 2.
=
; 4.
2.
=
; 4.
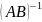 =
=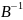 *
;
6.4)
О. Минором
k-того
порядка
произвольной матрицы А называется
определитель, составленный из элементов
матрицы, расположенных на пересечении
каких-либо k
строк и k
столбцов.
Например, в матрице А=
*
;
6.4)
О. Минором
k-того
порядка
произвольной матрицы А называется
определитель, составленный из элементов
матрицы, расположенных на пересечении
каких-либо k
строк и k
столбцов.
Например, в матрице А=
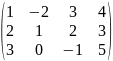 можно указать такие миноры:
1-го
порядка
можно указать такие миноры:
1-го
порядка
 :
:
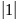 ;
;
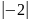 ;
;
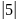 .
2-го
порядка
.
2-го
порядка
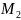 :
:
 ;
; ;
;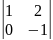 .
3-го
порядка
.
3-го
порядка :
:
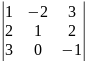 ;
;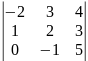 .
О.Рангом
матрицы А (rang
A)
называется максимальный порядок отличных
от нуля миноров этой матрицы
Пример:
Найти ранг
матрицы А=
.
Одним
из методов вычисления ранга матрицы
является метод
окаймляющих миноров.
Пусть в матрице найден минор k-того
порядка
.
О.Рангом
матрицы А (rang
A)
называется максимальный порядок отличных
от нуля миноров этой матрицы
Пример:
Найти ранг
матрицы А=
.
Одним
из методов вычисления ранга матрицы
является метод
окаймляющих миноров.
Пусть в матрице найден минор k-того
порядка
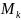 ,
отличный от нуля. Рассмотрим лишь те
миноры (k+1)-го
порядка, которые содержат в себе(окаймляют)
минор М: если все они равны нулю, то rang
A=k.
В противном случае среди окаймляющих
миноров найдется ненулевой минор
(k+1)-го
порядка, и вся процедура повторяется.
Фиксируем минор 2-го порядка, отличный
от нуля:
:
=
1-(-4)=5
,
отличный от нуля. Рассмотрим лишь те
миноры (k+1)-го
порядка, которые содержат в себе(окаймляют)
минор М: если все они равны нулю, то rang
A=k.
В противном случае среди окаймляющих
миноров найдется ненулевой минор
(k+1)-го
порядка, и вся процедура повторяется.
Фиксируем минор 2-го порядка, отличный
от нуля:
:
=
1-(-4)=5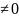 .
.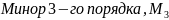 :
,
окаймляющий минор
,
также отличен от нуля:
=
-26. Поэтому rang
A=3
:
,
окаймляющий минор
,
также отличен от нуля:
=
-26. Поэтому rang
A=3
23
О.Пусть rang A =r. Любой минор r-го порядка матрицы А называется базисным минором. Строки и столбцы матрицы, участвующие в образовании базисного манора, также называются базисными.
Свойства
ранга матрицы:
1)
Если матрица имеет размер m×n,
то ранг её будет не больше минимального
из чисел m
и n:
rang
A
≤ min(m,n);
2)
rang
A=0
тогда и только тогда, когда А- нулевая
матрица;
3) Если А-квадратная матрица
n-го
порядка, то rang
A=n
тогда и только тогда, когда А-невырожденная
матрица, т.е
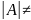 0
4)
Элементарные преобразования не меняют
ранга матрицы.
5) С помощью элементарных
преобразований любую матрицу можно
привести к ступенчатому виду.
6) Ранг
ступенчатой матрицы равен количеству
ее ненулевых строк.
0
4)
Элементарные преобразования не меняют
ранга матрицы.
5) С помощью элементарных
преобразований любую матрицу можно
привести к ступенчатому виду.
6) Ранг
ступенчатой матрицы равен количеству
ее ненулевых строк.




 Пример:
Вычислить ранг матрицы методом
элементарных преобразований:
А=
Пример:
Вычислить ранг матрицы методом
элементарных преобразований:
А= .
Решение.
Производя последовательно элементарные
преобразования, будем иметь:
̴
.
Решение.
Производя последовательно элементарные
преобразования, будем иметь:
̴
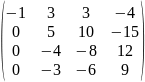 ̴
̴
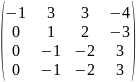 ̴
̴
̴
̴ .
Ранг
последней матрицы равен двум, следовательно,
таков же и ранг исходной матрицы, rang
A=2.
Заметим,
что ранги эквивалентных матриц равны
и обратно, т.е
̴
.
Ранг
последней матрицы равен двум, следовательно,
таков же и ранг исходной матрицы, rang
A=2.
Заметим,
что ранги эквивалентных матриц равны
и обратно, т.е
̴
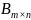
rangA=rangB.
Теорема
о ранге матрицы. Ранг
матрицы равен максимальному числу её
линейно независимых строк и
столбцов.
Теорема:
Базисные строки(столбцы) матрицы линейно
независимы.
Следствие:
Всякая строка(столбец) матрицы является
линейной комбинацией её базисных
строк(столбцов).
rangA=rangB.
Теорема
о ранге матрицы. Ранг
матрицы равен максимальному числу её
линейно независимых строк и
столбцов.
Теорема:
Базисные строки(столбцы) матрицы линейно
независимы.
Следствие:
Всякая строка(столбец) матрицы является
линейной комбинацией её базисных
строк(столбцов).
Литература:[1;c 59-67],[4;c 16-32].
24
