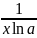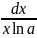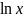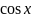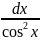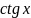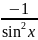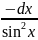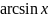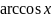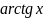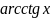- •Лекция 1. «Определители».
- •Практическое занятие №1.Определители. Вопросы для самопроверки.
- •Примеры решений задач.
- •Задания для аудиторной и домашней работы.
- •Ответы:
- •Задания для индивидуальной самостоятельной работы №1.
- •Практическое занятие №2.
- •3. Найти обратную матрицу для матрицы
- •Задания для аудиторной и домашней работы:
- •Лекция №3. Системы линейных уравнений (слу) и их решение.
- •Задачи для аудиторной и домашней работы.
- •Задания для индивидуальной самостоятельной работы.
- •Лекция 4. «Основы векторной алгебры».
- •Практическое занятие №4. Векторы. Линейные операции над векторами. Скалярное произведение векторов.
- •Задания для индивидуальной самостоятельной работы №4.
- •Лекция №6 Введение в математический анализ.
- •Лекция №8. Дифференциал. Теоремы о среднем. Правило Лопиталя. Формула Тейлора.
- •Практическое занятие №8. Дифференциал. Производные и дифференциалы высших порядков. Теоремы о среднем. Правило Лопиталя.
- •1. Найти дифференциал следующих функций:
- •2. Найти производные и дифференциал второго порядка функций:
- •3. Теоремы о среднем:
- •4. Правило Лопиталя:
- •5. Формула Тейлора и Маклорена:
- •2. Исследовать на экстремум функции:
- •4. Найти промежутки выпуклости и выгнутости графика функции
2. Исследовать на экстремум функции:
а) y= x3-2x2+3x+1
б)
y=1+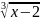 2\
2\
Решение
а) Находим производную y’=x2-4x+3
Приравниваем ее нулю и решаем уравнение x2-4x+3=0. Его корни x1=1,х2=3 –критические точки. Область определения функции (-∞;∞) разбивается на интервале (-∞;1).(1;3),(3; ∞). Исследуем критическую точку х1=1,определяя знак y’ вблизи этой точки слева и справа от нее: y'(1-0)>0, y’(1+0)<0, то при х1=1 функция имеет локальный максимум: ymax=y(1)= -2+3+1=2 . Аналогично ,для точки х2=3 получаем y’(3-0)<0,y’(3+0)>0. Следовательно, при х2=3 функция имеет локальный минимум: ymin=y(3)= *33-2*32+3*2-1=9-12+6-1=2
Б)Находим
производную y’=
*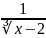 .
Производная не обращается в нуль ни при
каких значениях х и не существует лишь
при х=2.Это и есть критическая точка.
Определим знаки y’
вблизи точки х=2: y’(2-0)<0,y’(2+0)>0.
Следовательно ,при х=2 функция имеет
локальный минимум: ymin=y(2)=1.
.
Производная не обращается в нуль ни при
каких значениях х и не существует лишь
при х=2.Это и есть критическая точка.
Определим знаки y’
вблизи точки х=2: y’(2-0)<0,y’(2+0)>0.
Следовательно ,при х=2 функция имеет
локальный минимум: ymin=y(2)=1.
3.Исследовать на экстремум с помощью второй производной функции y=x+cos2x в интервале (0; ).
Решение.
а) Находим производную y’=1-2sin2x.
б)Определим критические точки ,принадлежащие заданному интервалу:
1-2sin2x=0
sin2x= 2x=(-1)n
2x=(-1)n +
+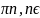 z,
x=(-1)n
z,
x=(-1)n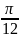 +
+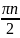 ,n
,n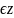 при
n=0,х1=
,
при n=1
при
n=0,х1=
,
при n=1
x2=
-
+
=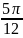
в)Находим y”=(1-2sin2x)’=-2(sin2x)’=-2cos2x*(2x)’=-4cos2x.
г)Найдем значение второй производной в критических точках:
135
y”(
)=-4cos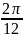 =-4cos
=-4*
=-4cos
=-4*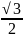 =-2
=-2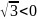 ,
то при х=
функция имеет локальный максимум:
ymax=y(
)=
+cos
=
+
,
то при х=
функция имеет локальный максимум:
ymax=y(
)=
+cos
=
+
y”(
)=-4cos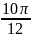 =-4cos
=-4cos =-
4(-cos
)=4*
=2
=-
4(-cos
)=4*
=2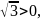 то
при х=
функция имеет локальный минимум :
то
при х=
функция имеет локальный минимум :
ymin=y(
)=
+cos
=
-

4. Найти промежутки выпуклости и выгнутости графика функции
y=x4-23-36x2-x+7.
Решение
а) Найдем вторую производную:
y’=4x3-6x2-72x-1, y”=12x2-12x-72. Y”=0 12x2-12x-72=0 или x2-x-6=0 x1=-2, x2=3.
б) Эти точки разбивает область определения функции на интервалы (-∞;-2),(-2;3) и (3;+ ∞)
в) Определим знаки второй производной в каждом интервале. Y”(-3)=72>0, то в промежутке (-∞;-2) y”>0, поэтому в этом интервале график функции выгнута. Y”(0)=-72<0, то в промежутке (-2;3) y”<0,следовательно ,в жтом интервале график функции выпукла y”(4)=72>0,значит,в интервале (3; ∞) график функции выгунта.
5. Найти точки перегиба кривой y=8/x24.
Решение.
а) Найдем вторую производную y’= - 16x/(x2+4)2
y”= - (16x/(x2+4)2)’= - (16*(x2+4)2-2(x2+4)*2x*16x)/(x2+4)4= 64x2-16(x2+4)/(x2+4)3=48x2-64/(x2+4)3
б)Найдем точки, в которых вторая производная обращается в нуль: y”=0
(48x2-64)/(x2+4)3=0
48x2-64=0
x2=
x1=
-
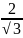 ,
x2=
.
,
x2=
.
в) Установим знаки второй производной функции в этих точках:
x1=
-
.
Если x
>
-
,например
, х=-2, то y”=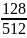 >0
;если x>-
,например, х=0,то y”=-1<0.
Итак, при x=
-
имеем точку перегиба. x2=
,
если х<
,
например х=2, то
>0
;если x>-
,например, х=0,то y”=-1<0.
Итак, при x=
-
имеем точку перегиба. x2=
,
если х<
,
например х=2, то
y"= >0.Значит, при х= также имеет точку перегиба.
г)Находим y( - )=(8/(- )2 +4)=8/ +4= .
Итак, (- ; .) и ( ; .) – точки перегиба.
6.
Найти асимптоты графика функции y=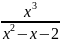
Решение.
Находим вертикальные асимптоты. Из определения асимптоты следует, что
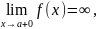 или
или
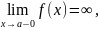 или
или
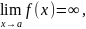 то
прямая х=а есть асимптота кривой y=f(x)
;
и обратно, если х=а естҗ асимптота ,то
выполняется одно из написанных равенств.
Область определения функции состоит
из интервалов :
(
x2-x-2≠0
x1≠-1
,х2≠2)
x
то
прямая х=а есть асимптота кривой y=f(x)
;
и обратно, если х=а естҗ асимптота ,то
выполняется одно из написанных равенств.
Область определения функции состоит
из интервалов :
(
x2-x-2≠0
x1≠-1
,х2≠2)
x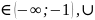 (-1;2),
(-1;2),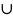 (2;
∞)
(2;
∞)
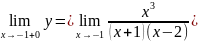 =
+∞,
=
+∞,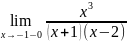 =-∞
=-∞
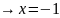 -
вертикальная асимптота.
-
вертикальная асимптота.
136
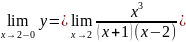 =
-∞,
=
-∞,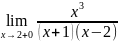 =+∞
=+∞
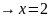 -
вертикальная асимптота.
-
вертикальная асимптота.
Находим наклонные асимптоты:
K=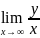 =
=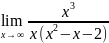 =
= =
=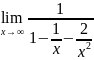 =1,
=1,
B=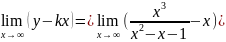 =
=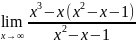 =
=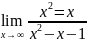 =
= =1.
=1.
Следовательно, прямая у=х+1 есть наклонная асимптота данной кривой.
Задания для аудиторный и домашний работы.
Найти интервалы монотонности и экстремума функций:
1.1. y=x5-2x3+x 1.2. y=x5-5x
1.3. y=x3- x2-6x+4 1.4. y=x3-3x2-45x+2
1.5.
y= 1.6. y=
1.6. y=
1.7.
y=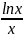 1.8. y=x2lnx
1.8. y=x2lnx
1.9. y=sinx+cosx 1.10. y=sin2x-x
2. Исследовать на экстремум с помощью второй производной следующие функции:
2.1.
y= -2x2+3x+1
2.2. y=x3-9x2+15x+3
-2x2+3x+1
2.2. y=x3-9x2+15x+3
2.3. y=x4-8x2+2 2.4. y= - x4+2x2+4
2.5. y=3x5-125x3+2160x 2.6. y=x5-2x3+x+6
2.7.
y= 2.8. y=
2.8. y=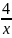 +
+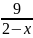
2.9.
y=x+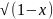 2.10. y=xln2x
2.10. y=xln2x
3.Исследовать на выгнутость, выпуклость и точки перегиба функции:
3.1. y=x3-3x2-18x+7 3.2. y= x3+2x2
3.3. y=x4+2x+3x+2 3.4. y=x4-x3+4x+3
3.5.y=x5-5x4+3x+5 3.6. y= x5+2x4-9x+6
3.7.y=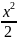 +lnx
3.8. y=
+lnx
3.8. y=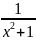
3.9.
y=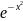 3.10. y=ln(1+x2)
3.10. y=ln(1+x2)
4. Найти асимптоты следующих кривых:
4.1.
y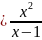 4.2. y
4.2. y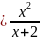
4.3.
y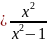 4.4. y
4.4. y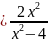
4.5.
y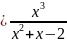 4.6. y
4.6. y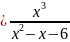
4.7.
y 4.8. y=
4.8. y=
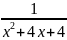
4.9. y=x+e-x 4.10. y=x+e-xsinx
137
ОТВЕТЫ:
1.1.
при х
(
-∞;-1)
(
-
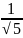 ;
;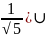 (1;
∞) функция возрастает; при х
(-1;
(1;
∞) функция возрастает; при х
(-1;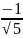 )
(
;1)
функция убывает. Ymax=y(-1)=0,
. Ymax=y(
)
(
;1)
функция убывает. Ymax=y(-1)=0,
. Ymax=y(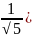 =
= ,
ymin=y(1)=0,
, ymin=y(
,
ymin=y(1)=0,
, ymin=y(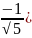 =
=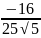 .
.
1.2. при х ( -∞;-1) (1; ∞) функция возрастает; . при х ( -1;1) функция убывает;
Ymax=y(-1)=4, ymin=y(1)=-4
1.3. . при х ( -∞;-1) (2; ∞) функция возрастает; . при х ( -1;2) функция убывает; Ymax=y(-1)=7,5, ymin=y(2)=-6
1.4. при х ( -∞;-3) (6; ∞) функция возрастает; . при х ( -3;6) функция убывает;
Ymax=y(-3)=83, ymin=y(5)=-173
1.5.
при х
(
-∞;-2)
(-2;
-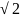 )
(
)
( )
функция возрастает; .
при х
(
-1;
)
функция убывает;Ymax=y(-
)=-17-12
,
ymin=y(
)=-17+12
,
)
функция возрастает; .
при х
(
-1;
)
функция убывает;Ymax=y(-
)=-17-12
,
ymin=y(
)=-17+12
,
1.6.
при х
(
-∞;-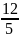 )
(0;
∞) функция возрастает; .
при х
(-
;0)
функция убывает;
)
(0;
∞) функция возрастает; .
при х
(-
;0)
функция убывает;
Ymax=y(-
)=
1.7. при х ( 0;е) функция возрастает; . при х ( е; ∞) функция убывает;
Ymax=y(е)=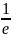
1.8.
при х
(
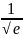 ;
∞) функция возрастает; .
при х
(
0;
)
функция убывает;
;
∞) функция возрастает; .
при х
(
0;
)
функция убывает;
ymin=у(
)=-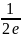 .
.
1.9.
при х
(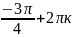 ;
;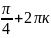 ;)к=0,
;)к=0,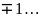 функция
возрастает;
при
х
(
;
функция
возрастает;
при
х
(
;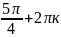 ;)к=0,
функция
убывает;
;)к=0,
функция
убывает;
Ymax=y(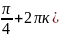 =
= ymin=у(
)=-
ymin=у(
)=-
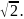
1.10
при х
(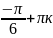 ;
;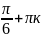 ;)к=0,
функция
возрастает;
при
х
(
;
;)к=0,
функция
возрастает;
при
х
(
; ;)к=0,
функция
убывает;
Ymax=y(
)=
;)к=0,
функция
убывает;
Ymax=y(
)=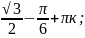 ymin=у(
)=
ymin=у(
)=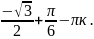
2.1. Ymax=y(1)= , ymin=y(2)=
138
2.2. Ymax=y(1)=10, ymin=y(5)=-22
2.3.
Ymax=y(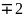 )=-14,
ymin=y(0)=2
)=-14,
ymin=y(0)=2
2.4.Ymax=y(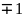 )=5,
ymin=y(0)=4
)=5,
ymin=y(0)=4
2.5. Ymax=y(3)=3834, Ymax=y(-4)=-3712; ymin=y(4)=3712; ymin=y(-3)=-3834
2.6.
Ymax=y(-1)=6,
Ymax=y( )=6+
)=6+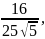 ymin=y(1)=6
ymin=y(1)=6 ymin=y
)=6-
ymin=y
)=6-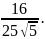
2.7. Ymax=y(1)= , ymin=y(-1)=-
2.8.
Ymax=y(-4)=
,
ymin=y(
)=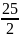
2.9.
Ymax=y(
)=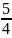
2.10. Ymax=y(е-2)=4е-2, ymin=y(1)=0
3.1. при х ( -∞;1) кривая выпукла; при х (1;∞) кривая выгнута ;точка (1;-13)- является точкой перегиба
3.2.
при х
(
-∞;-2)
кривая выпукла; при х
-2;∞)
кривая выгнута; точка
(-2;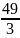 )-
является точкой перегиба
)-
является точкой перегиба
3.3. при х ( -∞;-1) (0; ∞) кривая выгнута; при х (-1;0) кривая выпукла; точки (0;2) и(-1;-2) являются точками перегиба кривой
3.4.
при х
(
0;
)
кривая выпукла; при х
(-∞;0)
(
;
∞) кривая выгнута ;точки
(0;3)и (
; )-
являются точками перегиба кривой
)-
являются точками перегиба кривой
3.5. при х ( -∞;3) кривая выпукла; при х (3;∞) кривая выгнута ;точка (3;-149)- является точкой перегиба.
3.6.
.
при х
(
-∞;-6)
кривая выпукла; при х
(-6;∞)
кривая выгнута ;точка
(-6;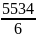 )-
является точкой перегиба
)-
является точкой перегиба
3.7. при х ( 0;1) кривая выпукла; при х (1;∞) кривая выгнута ;точка (1; )- является точкой перегиба
3.8.
при х
(
-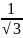 ;
)
кривая выпукла; при х
(-∞;-
)
(
;
∞) кривая выгнута ;точки
;
)
кривая выпукла; при х
(-∞;-
)
(
;
∞) кривая выгнута ;точки
(-
;
)
и (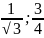 )
- являются точками перегиба.
)
- являются точками перегиба.
139
3.9.
при х
(
- ;
)
кривая выпукла; при х
(-∞;-
)
(
;
∞) кривая выгнута; точки
;
)
кривая выпукла; при х
(-∞;-
)
(
;
∞) кривая выгнута; точки
(-
;
)
и ( )- являются точками перегиба.
)- являются точками перегиба.
3.10. при х ( -∞;-1) (1; ∞) кривая выгнута; при х (-1;1) кривая выпукла; точки (-1;ln2) и(1;ln2) являются точками перегиба кривой.
4.1 x=1 4.2.х=2 4.3.х=-1 , х=1,у=1 4.4.х=-2, х=2,у=2 4.5.х=-2,х=1,у=х-1 4.6.х=-2,х=3,у=х+1
4.7.х=1,у=0 4.8.х=-2,у=0 4.9.у=х 4.10.у=х
Задания для индивидуальной самостоятельный работы №9.
В каждом задании N-номер вашего варианта.
1.Найти интервалы монотонности экстремумы функции
Y=x3+Nx2-(2N+3)x+N+4
2. Исследовать на экстремум с помощью второй производной
Y=
x4-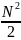 x2+N2
x2+N2
3.Исследовать на выгнутость, выпуклость, и точки перегиба функции
Y=
x4+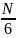 x3-
x3-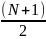 x2+2x+1
x2+2x+1
4. Найти асимптоты кривой
Y=
5.Глобальные экстремумы функции на отрезке, их нахождение для дифференцируемой функции.
Нулевые
варианты контрольной работы
Вариант №1.
1.Вычислить
определитель четвёртого порядка.
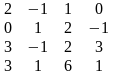
140
2.Решить
по формулам Крамера систему
уравнений.

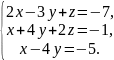 3.Вычислите
3.Вычислите
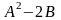 ,
еслиА=
,
еслиА=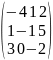 ,В=
,В= 4.Найдите
длину медианы А
М
треугольника с вершинами А(2;-2;0),
В(7;-3;1), С(1;-1;5) .
5.Найти
угол между прямой 3х+2y+4=0,
и
прямой, проходящей через точкиМ
4.Найдите
длину медианы А
М
треугольника с вершинами А(2;-2;0),
В(7;-3;1), С(1;-1;5) .
5.Найти
угол между прямой 3х+2y+4=0,
и
прямой, проходящей через точкиМ (2;-2),
М
(2;-2),
М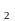 (4
; -3).
6.Найти
область определения функции.
(4
; -3).
6.Найти
область определения функции.
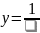 +
+
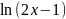 7.Вычислить
предел
7.Вычислить
предел
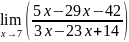 .
8.Найти значение производной
функции
.
8.Найти значение производной
функции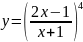 при
x=1.
9.Вычислить
предел ,применяя правило Лопиталя
при
x=1.
9.Вычислить
предел ,применяя правило Лопиталя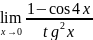 10.Найти
сумму ординат точек экстремумов функции
y=
10.Найти
сумму ординат точек экстремумов функции
y=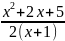 .
.
Ответы
Вариант
1 .
1.
0;
6.(
;2)
2.
(-1; 1; -2) 7.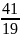 3.
3.
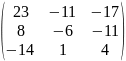 .
8.
4.
.
8.
4.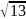 9.8
5.arctg
9.8
5.arctg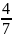 10.
0.
10.
0.
141
Вариант
№ 2.
1.Вычислить
определитель
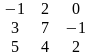 ,его
минор
,его
минор
 и
алгебраическое дополнение
.
2.Решать
методом Гаусса систему уравнений
и
алгебраическое дополнение
.
2.Решать
методом Гаусса систему уравнений
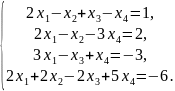 3.Задана
матрица А=
3.Задана
матрица А= .Матрица
+3А
имеет вид
.Матрица
+3А
имеет вид
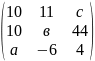 .Найтиа,в,с.
4.Найти
.Найтиа,в,с.
4.Найти
 (3
-
(3
-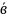 ),если
=(0;
2; 3),
=(-1;
3; -2)
.
5.Даны вершины треугольникаА(-7;
3), В(5; -2), С(8;2).Найти
координаты точки пересечения медианы
ВDи
высотыCE.
6.Найти
область определения функции
),если
=(0;
2; 3),
=(-1;
3; -2)
.
5.Даны вершины треугольникаА(-7;
3), В(5; -2), С(8;2).Найти
координаты точки пересечения медианы
ВDи
высотыCE.
6.Найти
область определения функции
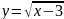 +arcsin
+arcsin .
7.Вычислить
предел
.
7.Вычислить
предел
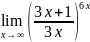 .
8.Найти
значение производной функции, заданной
параметрический
.
8.Найти
значение производной функции, заданной
параметрический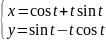 при
t=
.
9.Составить
уравнение касательной и нормали к кривой
y=
при
t=
.
9.Составить
уравнение касательной и нормали к кривой
y=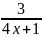 в
точке
=2
10.С
помощью дифференциала вычислить tg
в
точке
=2
10.С
помощью дифференциала вычислить tg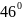 .
.
142
Вариант
2.
1. ∆= -40,
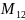 =
-23,
=14
6.
=
-23,
=14
6.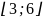 2.(0;
2;
;
2.(0;
2;
;
 ).
7.
).
7.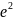 3.а=
-2,
в=4
,с=42
8.
1
4.
3.а=
-2,
в=4
,с=42
8.
1
4.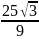 9.
4x+27y-17=0;
81x-12y-158=0
5.
9.
4x+27y-17=0;
81x-12y-158=0
5.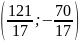 10.
1,0355
10.
1,0355
Примерный вариант итоговой зачётной или экзаменационной работы. 1.Вычислить определители 3-го порядка, миноры, алгебраические дополнения. 2.Вычислить определитель 4-го порядка. 3.Выполнить действия над матрицами. 4.Решить СЛУ методом Крамера. 5.Решить СЛУ методом Гауса. 6.Вычислить обратную матрицу. 7.Вычислить угол между векторами; проекцию вектора на ось. 8.Составить уравнения сторон, медиан и высот 9.Найти область определения функции. треугольника. 10.Вычислить пределы. 11.Найти значение производной функции в точке. 12.Найти интервалы монотонности и экстремумы функции. 13.Найти интервалы выпуклости ,вогнутости и точки перегиба функции. 14.Найти наименьшее и наибольшее значение функции на отрезке. 15.Вычислить предел, пользуясь правилом Лопиталя. 16.Применяя теоремы Ролля, Лагранжа ,найти среднюю точку функции.
Преобразование произведения функций.
143
Приложение
№1.
Формулы
сокращённого умножения
1.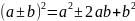 2.
2.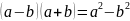 3.
3.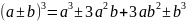 4.
4. )=
)=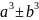 Формула
тригонометрии:
Функции
одного угла.
1.
Формула
тригонометрии:
Функции
одного угла.
1.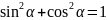 2.
tg
2.
tg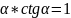 3.1+
3.1+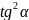 =1/
=1/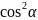 4.1+
4.1+ Формулы
сложения.
5.sin(
Формулы
сложения.
5.sin(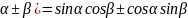 6.cos(
6.cos(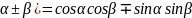 7.
7. Формулы
двойных, половинных, тройных углов.
8.sin2
Формулы
двойных, половинных, тройных углов.
8.sin2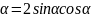 9. cos2
9. cos2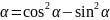 10.tg2
10.tg2 11.cos
=
11.cos
=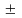
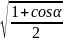 12.sin
=
12.sin
=
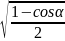 13.tg
=
13.tg
=
 14.sin
3
=3sin
-4
14.sin
3
=3sin
-4 15.cos3
=4
15.cos3
=4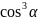 -3cos
Преобразование
суммы функций в
произведение.
16.cos
+cos
-3cos
Преобразование
суммы функций в
произведение.
16.cos
+cos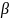 =2cos
=2cos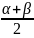 cos
cos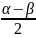 17.cos
-cos
=-2sin
sin
18.sin
+sin
=2sin
cos
19.sin
-sin
=2sin
cos
144
17.cos
-cos
=-2sin
sin
18.sin
+sin
=2sin
cos
19.sin
-sin
=2sin
cos
144
20.
tg
tg
=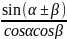 21.
cos
21.
cos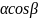 =
(cos(
=
(cos(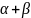 )+cos(
)+cos(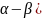 22.sinsin
=
(cos(
22.sinsin
=
(cos(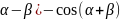 23. sin
cos
=
(sin(
23. sin
cos
=
(sin( Понижение
степени.
24.
=
(1+cos2
)
25.
Понижение
степени.
24.
=
(1+cos2
)
25.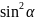 =
(1-cos2
)
26.
sin
cos
=
sin2
=
(1-cos2
)
26.
sin
cos
=
sin2
Значения тригонометрических функции некоторых углов.
|
0 |
|
/4 |
|
/2 |
|
|
|
|
sin |
0 |
1/2 |
1/ |
|
1 |
/2 |
0 |
-1 |
0 |
cos |
1 |
/2 |
|
1/2 |
0 |
-1/2 |
-1 |
0 |
1 |
tg |
0 |
1/ |
1 |
|
|
- |
0 |
|
0 |
ctg |
|
|
1 |
1/ |
0 |
1/ |
|
0 |
|
Формулы приведения.
Функция |
|
|
|
2 |
sin |
+cos |
|
-cos |
|
cos |
|
-cos |
sin |
|
tg |
|
|
|
|
Ctg |
|
|
|
|
145
Приложение №2 Таблица производных и дифференциалов основных элементарных функций.
№ |
f(x) |
f '(x) |
d f(x) |
1 |
( |
|
dx |
2 |
(0< |
|
|
3 |
|
|
dx |
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
146
Основные
правила дифференцирования элементарных
функций.
1.
(C)
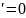 ,
C=const 2. (f
,
C=const 2. (f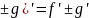 3.
(Cf)
'=C
f
' 4.(f
3.
(Cf)
'=C
f
' 4.(f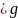 )
'=f
'g
+fg
'
5.
)
'=f
'g
+fg
'
5.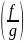 '
'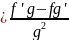 ,
g≠0
6.
,
g≠0
6. ,
g
7.(f
((x)))
'
,
g
7.(f
((x)))
'
 ((x))
'(x)или
((x))
'(x)или производная
сложной функции.
8. (
производная
сложной функции.
8. (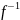 (y))
'
(y))
' или
или
 производная
обратной функции.
9.
производная
обратной функции.
9. производная
функции, заданной параметрический .
производная
функции, заданной параметрический .
147
Литература 1. Баврин И.И. Высшая математика: Учебник. 3-е изд., стереотип .-М.;, Издательский центр «Академия»,2003.-616с. ISBN-5-7695-0612-1. 2. Михеев В.И., Павлюченко Ю.В. Высшая математика, краткий курс. - М.: Физматлит. 2007. - 200 с. ISBN-5-978-9221-0772-3. 3. Шипачев В.С. Задачник по высшей математике: Учебное пособие. - М.: Высш. шк. , 2003.- 304 с. ISBN-5-06-003575-1. 4. Шапкин А.С. Задачи с решениями по высшей математике, теории вероятностей и математической статистике: Учебное пособие-3-е изд.- М.: « Дашков и К°», 2006.-432 с. ISBN-5-94798-957-3. Дополнительная литература 1. Абрамова В.В. , Зайниев Р.М. , Сафаров А.С. . Сборник заданий по математике/Под ред. Котляра Л.М. и Зайниева Р.М. - 2-е изд. , перераб. и доп. - Набережные Челны: Изд-во ИНЭКА , 2006 - 475 с. 2. Н.М. Миназетдинов , А.С. Сафаров. Аналитическая геометрия на плоскости: Учебное пособие. Набережные Челны: Изд-во НЧИ К(П)ФУ, 2014 - 74 с. 3. Н.М. Миназетдинов , А.С. Сафаров. Аналитическая геометрия в пространстве: Учебное пособие. Набережные Челны: Изд-во НЧИ К(П)ФУ, 2014 - 67 с. 4. Зайниев Р.М. , Миназетдинов Н.М. , Сафаров А.С. Векторная алгебра и аналитическая геометрия: учебное пособие по математике для самостоятельной работы. Набережные Челны: Издательско-полиграфический центр НЧИ К(П)ФУ, 2015. - 88 с. 5. Габбасов Н.С. , Губочкина Н.И. , Зайниев Р.М. Вычисление пределов функции: методические указания и контрольные задания. - Наб.Челны: Из-ко полиграф. центр НЧИ КФУ, 2015 - 40 с. 6. Л.Ю. Грудцина , М.Я. Товштейн. Курс лекций по линейной алгебре: учебное пособие. фил. Казан. гос. ун-та. - Набережные Челны: Лаб. операт. полиграфии , 2007. - 58 с.
148

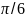
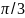
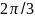
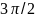
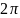

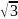 /2
/2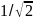

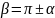
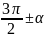
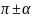
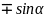
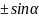

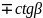
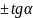
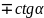
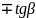

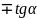
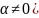
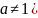
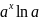
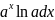
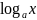 (0<a
(0<a