Казанский (Приволжский) федеральный университет Набережночелнинский институт А.С. Сафаров Математика. 1 часть Учебное пособие Набережные Челны - 2017

УДК 51(075.8) ББК 22.1 я 73 С 21 Печатается по решению редакционно-издательского совета Набережночелнинского института К(П)ФУ Рецензенты: кандидат физ.-мат. наук, доцент Углов А.Н., кандидат физ.-мат. наук, доцент Шакиров И.А. С21 Сафаров А.С. Математика. 1 часть: учебное пособие- Набережные Челны: Изд-во НЧИ К(П)ФУ, 2017.- 148 с. Учебное пособие предназначено для студентов всех направлений для которых предусмотрено краткий курс высшей математики. Первая часть содержит 9 лекций и 9 практических занятий. Наличие в пособии устных вопросов, индивидуальных заданий для самостоятельных работ, образов решение задач и контрольных работ поможет студентам подготовиться к зачёту (или экзамену). Адресовано студентам младших курсов и преподавателям вузов. УДК 51(075.8)

ББК 22.1 я 73 © А.С.Сафаров, 2017.

©НЧИ К(П)ФУ, 2017. Оглавление Предисловие................................................................................. 5 Введение..............................................................................................7 1.Лекция №1. Определители...................................................9 2.Практическое занятие № 1.Определители …....................14 1.1. Вопросы для самопроверки........................................................14 1.2.Примеры решения задач..............................................................15 1.3.Задания для аудиторной и домашней работы...........................17 1.4.Задания для индивидуальной самостоятельной работы №1..17 3.Лекция №2. Матрицы...........................................................18 4.Практическое занятие №2. Матрицы..................................19 2.1.Вопросы для самопроверки.........................................................25 2.2 Примеры решения задач..............................................................26 2.3 Задания для аудиторной и домашней работы…........................28 2.4. Задания для индивидуальной самостоятельной работы №2.29 5. Лекция №3. Системы линейных уравнений......................31 6.Практическое занятие №3.СЛУ………………............................39 3.1. Вопросы для самопроверки.......................................................39 3.2 Примеры решения задач..............................................................40 3.3 Задания для аудиторной и домашней работы...........................43 3.4 Задания для индивидуальной самостоятельной работы №3..47

7. Лекция №4.Векторная алгебра............................................48 8.Практическое занятие №4. Векторная алгебра..................55 4.1 Вопросы для самопроверки.............................................................55 4.2 Примеры решения задач………..........................................................56 4.3 Задания для аудиторной и домашней работы................................60 4.4 Задания для индивидуальной самостоятельной работы №4.......63 2 9. Лекция №5. Прямая на плоскости. Плоскость и прямая в пространстве...........................................................................................64 10.Практическое занятие №5. Прямая на плоскости. Плоскость и прямая в пространстве..........................................................................73 10.1. Вопросы для самопроверки.........................................................73 10.2 Примеры решения задач................................................................74 10.3 Задания для аудиторной и домашней работы.............................82 10.4 Задания для индивидуальной самостоятельной работы №5.....85 11.Лексия №6. Функции: предел и непрерывность...........................85 12. Практическое занятие №6. Свойства основных элементарных функций. Предел и непрерывность......................................................94 12.1 Вопросы для самопроверки..........................................................94 12.2 Примеры решения задач................................................................96 12.3 Задания для аудиторной и домашней работы............................100 12.4 Задания для индивидуальной самостоятельной работы №6…105 13.Лекция №7. Дифференциальное исчисление функций одной переменной...........................................................................................106 14.Практическое занятие №7. Производная функции.....................112 14.1. Вопросы для самопроверки........................................................112 14.2 Примеры решения задач...............................................................113 14.3 Задания для аудиторной и домашней работы............................115 14.4 Задания для индивидуальной самостоятельной работы № 7..116 15.Лекция №8. Дифференциация. Теорема о среднем. Правило Лопиталя. Формула Тейлора...........................................................117 16.Практическое занятие №8..........................................................122 16.1. Вопросы для самопроверки.........................................................122 16.2 Примеры решения задач...............................................................124 16.3 Задания для аудиторной и домашней работы............................126 16.4 Задания для индивидуальной самостоятельной работы №8…129 3 17. Лекция №9. Исследование функций при помощи производных............................................................................................130 18. Практическое занятие №9...................................................134 18.1 Вопросы для самопроверки............................................................134 18.2 Примеры решения задач.................................................................135 18.3 Задания для аудиторной и домашней работы..............................137 18.4 Задания для индивидуальной самостоятельной работы №9……140

Нулевые варианты контрольной работы……………………………….140 Примерный вариант итоговой зачётной или экзаменационной работы…………………………………………………………………………………………….143 19.Приложения.................................................................................144 20.Литература.....................................................................................148 Дополнительная литература........................................................148

4

Предисловие. В связи с очередным реформированием образовательной системы России, время, отводимое на аудиторные занятия по общеобразовательным дисциплинам, в том числе по математике, резко сократилось. Требования компетентностного подхода к изучению естественно- научных дисциплин выполнимы только при переходе от пассивных форм обучения к активной, творческой и индивидуальной работе со студентами путём расширения их самостоятельной работы. Такой путь развития в высшем образовании предполагает новое методическое обеспечение учебного процесса, подготовки новых методических пособий и электронных образовательных ресурсов, обеспечивающих самостоятельное выполнение индивидуальных работ студентами. Учебное пособие предназначено для студентов нематематических направлений подготовки, где предусмотрено краткий курс высшей математики. Пособие состоит из введения, 9 лекций и 9 практических занятий, включающих следующие разделы математики: основы линейной алгебры, основы векторной алгебры и аналитической геометрии, введение в математический анализ, дифференциальное исчисление функции одной переменной. В лекциях теоретический материал изложен доступным языком, применяя графические иллюстрации и примеры. Каждое практическое занятие начинается с вопросов для самопроверки: эти вопросы нужны для проверки подготовленности студентов к практическим занятиям. В пункте "примеры решения задач" указываются решения типичных задач, чтобы объяснить применение изученных математических методов к решению задач. В пункте "задания для аудиторной и домашней работы" содержится свыше пятисот задач по высшей математике, которые могут быть использованы как для аудиторных самостоятельных работ, так и для домашних работ. Ко всем заданиям даны ответы. В пункте "задание для индивидуальной самостоятельной работы" прилагается 5

индивидуальные самостоятельные задания для каждого студента. Указаны теоретические вопросы для самостоятельного изучения, приведены нулевые варианты контрольной работы. Автор считает, что умение самостоятельно решать типовые задачи различной степени трудности является важным критерием успеха студента при изучении математики. Введение содержит рекомендации студентам, как изучать математику по данному пособию.

6

Введение Данное пособие ставит своей целью оказать помощь студентам в овладении системы знаний и умений по математике в объёме действующей программы. При этом основной формой учебного процесса является индивидуальная самостоятельная работа студентов с книгой. Следует заметить, что нет единой системы самостоятельной работы над книгой, которая годилась бы во всех деталях для всех. И все же имеются некоторые общие, проверенные практикой ,рекомендации самостоятельной работы над книгой. Первая из них состоит в том, что студент должен посещать все аудиторные занятия. Поучаствовав в лекции(или в практическом занятии), в тот же день, приведите в порядок свои записи, воспользовавшись учебным пособием. Главное заключается не в самом процессе чтения, а в усвоении прочитанного, в умении понять основное содержание темы, выделить наиболее важные факты, формулы, которые нужно запомнить. Решите самостоятельно приводимые в пособии примеры: при этом вспомните похожую задачу, необходимые формулы, которые могут иметь отношение к ее решению. Если зашли в тупик, то за советом обращайтесь к преподавателю. Вторая рекомендация состоит в том, что самостоятельная работа над книгой должна быть систематической. Любой непонятный вопрос приводит к другим неясностям, в итоге - в очень трудную науку. Только при регулярной и эффективной самостоятельной работе над книгой не возникнут проблемы в знаниях и умениях. В самостоятельной работе над книгой большое значение имеет умение конспектировать изученный материал. Главная цель конспекта-усвоение и запоминание прочитанного. Конспект- это основное пособие для студентов при подготовке к зачётам или экзаменам. Только усвоив теоретический материал, решите новые задачи по данной теме. Третья рекомендация состоит в том, что самостоятельная работы над книгой должна сопровождаться повторением и запоминанием учебного материала. Важнейшим средством предотвращения забывания является повторение. При повторении очень полезно тренироваться в

7

словесном изложении математических формул, самостоятельном выводе

их, а также в доказательстве теорем без использования книги. Чтобы надолго запомнить учебный материал, необходимо найти в нём так называемые опорные пункты. Это основные определения и теоремы, между которыми установлена логическая связь . Следовательно, сначала следует разобраться в учебном материале, а далее ставит цель его запомнить. Четвёртая рекомендация состоит в том, что самостоятельная работа над книгой должна сопровождаться с повторением школьной математикой. Автор уверен в том, что многие упущения и недоработки в полученном в своё время школьном образовании могут быть устранены в высшей школе. Для этого студент должен быть готовым приложить необходимые усилия, чтобы освежить в памяти соответствующие места школьного курса математики. Автор выражает благодарность рецензентам за высказанные ценные замечания и полезные советы по содержанию учебного пособия.

8

Лекция 1. «Определители».

1. Определители 2-го и 3-го порядка, их вычисление. Основные свойства определителей.

2. Минор и алгебраическое дополнение элемента определителя.

3. Теорема о разложении определителя по элементам строки или столбца.

4. Понятие определителя n-го порядка.

1.1. О. Определителем второго порядка называется число, обозначаемое символом 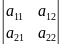и вычисляемое равенством . (1)

Числа 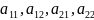называются элементами определителя.

П. 1. .

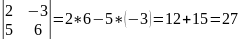2. .

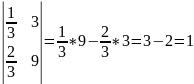Обратим внимание на то, что в выражении определителя сомножителями в каждом из произведений служат числа, стоящие в разных строках и разных столбцах.

О. Определителем третьего порядка называется число, обозначаемое 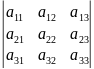и определяемое равенством 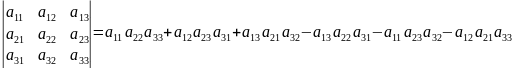. (2)

П. .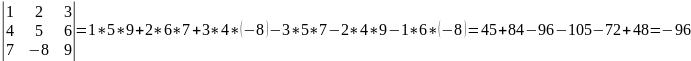

Чтобы запомнить, какие произведения в правой части равенства (2) берутся со знаком «+», а какие со знаком «–», полезно использовать следующее правило треугольников:

Заметим, что основания треугольников параллельны главной (соответственно побочной) диагонали определителя.

Легко проверяются основные свойства определителя:

1. Величина определителя не изменится, если его строки и столбцы поменять местами, т.е. .

2. Перестановка двух строк или двух столбцов определителя равносильна умножению его на –1.

9

3. Если определитель имеет два одинаковых столбца (или строки), то он равен нулю.

4. Умножение всех элементов одного столбца (или строки) определителя на любое число m равносильно умножению определителя на это число m.

5. Если все элементы некоторого столбца (или строки) определителя равны нулю, то и сам определитель равен нулю.

6. Если элементы двух столбцов (или строк) определителя пропорциональны, то определитель равен нулю.

7. Если каждый элемент некоторого столбца (или строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в этом столбце (строке) имеет первые из упомянутых слагаемых, а другой – вторые; элементы, стоящие на остальных местах, у всех определителей одни и те же: .

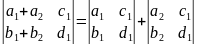8. Если к элементам некоторого столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки), умноженные на любой общий множитель m, то величина определителя не изменится: .

1.2 Элементы определителя третьего порядка обозначим , ij=1, 2, 3. При этом первый индекс i номер строки, а второй индекс j – номер столбца, к которому принадлежит данный элемент. Будем также говорить, что элемент находится на пересечении i-ной строки и j-ного столбца. Элементы определителя 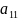, , 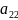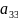образуют главную диагональ, а элементы 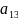, , 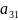– побочную.

О. Минором элемента определителя называется определитель, получаемый из данного определителя вычёркиванием строки и столбца, на пересечении которых этот элемент расположен. Минор элемента обозначается через .

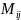П. Минорами определителя второго порядка являются: , , ,

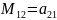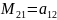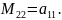
Минорами элементов , 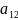, определителя третьего порядка являются:

,

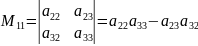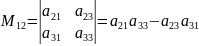, (3)

.

10

О. Алгебраическим дополнением элемента определителя называется минор этого элемента, умноженный на 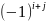. Алгебраическое дополнение элемента обозначается через .

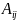Итак, по определению: . (4)

Отсюда

В частности, , , .

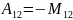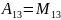П. Дан определитель . Вычислить определитель ∆, минор элемента , алгебраическое дополнение .

Решение:

.

.

.

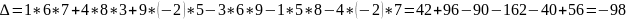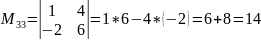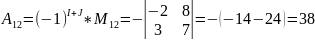1.3 Формулу (2) можно переписать в виде:

.

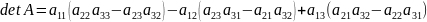Учитывая равенства (3)

,

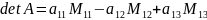или

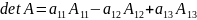, (5)

т.е. определитель 3-его порядка равен сумме произведений элементов первой строки на их алгебраические дополнения. Аналогичные формулы справедливы для других строк и столбцов определителя 3-его порядка. Это свойство верно также для определителей n-го порядка.

Свойство 9 (Теорема Лаиласа).

Определитель n-го порядка равен сумме произведений элементов любой строки на их алгебраические дополнения:

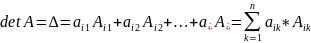, где i=1, 2, 3,..,n. (6)

Эта формула называется разложением определителя по строке i.

Определители n-го порядка равен сумме произведений элементов любого столбца на их алгебраические дополнения:

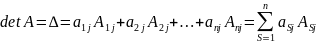, где j=1, 2, 3,..,n. (7)

11

Эта формула называется разложением по столбцу j.

Значение теоремы Лаиласа состоит в том, что она позволяет свести вычесления определителей n-го порядка к вычислению определителей (n-1)-ного порядка.

П. Вычислить определитель 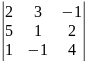, используя формулу разложения по первой строке и второму столбцу.

Решение:

а) .

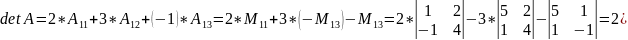б) .

Заметим, что если в определителе все элементы некоторого столбца (строки), кроме одного элемента, равны нулю, то вычислению этого определителя сводится к вычислению одного его определителя (n-1)-го порядка.

П.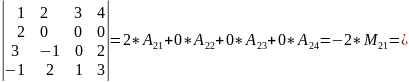

.

Мы разложили определитель четвертого порядка по элементам второй стоки, где имеются три нулевые элемента, вычисление этого определителя свели к вычислению определителя третьего порядка.

Заметим, что если элементы определителя, стоящие ниже (выше) главной диагонали определителя, равны нулю, то определитель равен произведению элементов главной диагонали.

Свойство 10.

Сумма произведений элементов некоторой строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю: , (8)

где ; I, j = 1, 2, …, n.

1.4 О. Определителем n-го порядка называется число, записываемое в виде

12

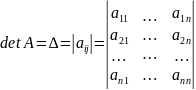, (9)

и вычисляемое по данным числам по следующему закону:

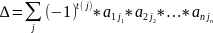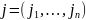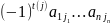∆ — есть сумма , распространённая на всевозможные различные перестановки из чисел 1, 2, …, n. Число t(j) равно числу транспозиций, которые нужно сделать, чтобы перейти от основной перестановки 1, 2, …, n к перестановке . Произведение называется членом определителя.

Определители n-го порядка удовлетворяют свойствам 1-10, перечисленным выше.

П. Вычислить определитель

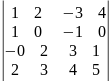
а) разложив по элементам второй строки;

б) применив свойство 8.

Решение:

а)

.

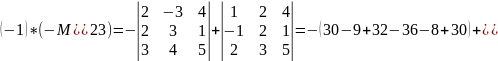
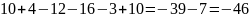б)

.

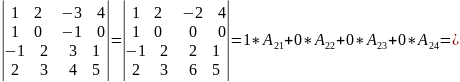
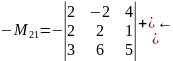
Необходимость введения определителя тесно связана с решением систем линейных уравнений.

Литература:[1;с 68-72],[2;c 33-36],[3;c 123-127],[4;c 16-32]

13