2 Практическая часть
Определить
Ц.Д.(миллиамперметра)=
Δп.п.(миллиамперметра)=
Подключить катушку-моток 2(см. Рис. 3) к зажимам миллиамперметра.
Внести северный полюс дугообразного магнита в катушку вдоль её оси. В последующих опытах полюса магнита перемещать с одной и той же стороны катушки, положение которой не изменяется. Проверить соответствие результатов опыта с таблицей 1.
Удалить из катушки северный полюс дугообразного магнита. Результаты опыта представить в таблице 2.
Таблица 2
Внести в катушку южный полюс дугообразного магнита. Результаты опыта представить в таблице 3.
Таблица 3
Удалить из катушки южный полюс дугообразного магнита. Результаты опыта представьте в таблице 4.
Таблица 4
Сделать вывод по результатам работы.
Контрольные вопросы
В чём состоит явление электромагнитной индукции?
Каков механизм возникновения э.д.с. индукции?
Сформулируйте закон Фарадея для э.д.с. индукции.
В чём заключается правило Ленца?
Что такое самоиндукция?
Почему при отключении от сети лампочки накаливания иногда перегорают?
Литература
Дмитриева В.Ф. Физика. - М.: Издательский центр «Академия», 2013,
гл. 13, § 13.1-13.4.
Лабораторная работа 9
Тема: Изучение зависимости периода колебаний нитяного маятника от длины нити.
Цель: выяснить, как T свободных колебаний нитяного маятника зависит от его длины.
Оснащение: штатив с держателем, шарик на нити, измерительная лента или линейка, секундомер.
Порядок выполнения работы:
Повторить изученный ранее теоретический материал.
Ознакомиться с описанием работы.
Выполнить практическую часть.
Сделать вывод по результатам произведенных расчетов.
Письменно ответить на контрольные вопросы.
1.Теоретическая часть
Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити. Моделью может служить тяжёлый шарик, размеры которого весьма малы по сравнению с длинной нити, на которой он подвешен (не сравнимы с расстоянием от центра тяжести до точки подвеса).
Учёные Галилей, Ньютон, Бессель и др. установили следующие законы колебания математического маятника:
I. Период колебания математического маятника не зависит от массы маятника и от амплитуды ( если угол размаха не превышает 10).
II. Период колебания математического маятника прямо пропорционален квадратному корню из длины маятника l и обратно пропорционален квадратному корню из ускорения свободного падения g.
.
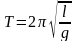