21

Конспект лекций 5 колебания и волны механические колебания

§1. Гармонические колебания и их характеристики

Гармонические колебания – это колебания, происходящие по закону cos или sin.

Графически гармонические колебания изображаются методом векторных диаграмм.

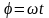
отсюда

В общем виде уравнение гармонического колебания записывают в виде:

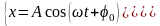
х – смещение колеблющейся точки от положения равновесия, [м];

А – амплитуда колебания (max смещения), [м];

ω₀ – круговая (циклическая) частота, [рад/с];

t – текущее время, [с];

φ₀ – начальная фаза колебания (она определяет смещение, скорость и ускорения точки в момент времени t = 0), [рад];

φ = фаза колебания (определяет смещение, скорость и ускорение точки в момент времени t), [рад].

Положение колеблющейся системы повторяется через промежуток времени Т (период колебаний). При этом фаза получает приращение 2π.

t – время;

N – число полных колебаний;

ν – частота.

§2. Скорость и ускорение при колебательном движении

Пусть

- скорость, [м/с];

или – ускорение, [м/с²].

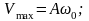
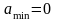
Амплитуды колебаний скорости и ускорения соответственно равны А₀ и А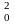 . Фаза колебаний скорости отличается от фазы колебаний величины отклонения на /2, а фаза колебаний ускорения --на . Следовательно, в моменты времени, когда х=0, dх/dt приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то d²х/dt² приобретает наибольшее положительное значение :

§3. Уравнение гармонического колебания в дифференциальной форме

-

Отсюда дифференциальное уравнение гармонического колебания:

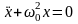или .

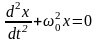Уравнение является решением дифференциального уравнения.

Гармоническим колебанием называется колебание, у которого ускорение прямопропорционально смещению.

§4. Динамика колебаний

1. Сила, действующая на колеблющуюся точку

, тогда

или

- II закон Ньютона

(при )

(при )

2. Кинетическая энергия

3. Полная или суммарная энергия

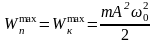
4. Потенциальная энергия

;

§5. Гармонический осцилятор. Маятники

Гармонический осцилятор – это система, совершающая колебания, описываемые уравнением вида

Это математическая модель периодического движения во многих задачах классической и квантовой физики.

Примером гармонического осцелятора являются пружинный, математический и физический маятники.

1 . Пружинный маятник— это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины.

Уравнение движения маятника

где циклическая частота колебаний;

Так как , то 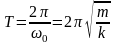- период пружинного маятника

- потенциальная энергия пружинного маятника