21

Конспект лекций 1 механика кинематика

§1. Основные понятия кинематики

Материальная точка — тело, размерами которого можно пренебречь по сравнению с расстоянием до других тел, с которыми оно взаимодействует.

Тело отсчета – тело, относительно которого определяется положение материальной точки.

Система отсчета – система координат, привязанная к телу отсчета + часы.

Положение материальной точки в пространстве можно задать одним векторным уравнением: где радиус-вектор;

- единичные векторы (орты);

x, y, z – координаты точки

В скалярной форме .

Рассмотрим движение материальной точки в системе координат из т. А в т.В.

Траектория – форма линии АВ, вдоль которой движется тело (безразмерная величина).

Перемещение r = r — r_{0 ,} [м]– кратчайшее расстояние между начальным и конечнм положением точки (векторная величина)

Длина пути s , _, [м] - длина траектории АВ (скалярная величина).

• Перемещение и путь равны по величине только в одном случае: если тело движется по прямой, не меняя направления движения.

• Во всех остальных случаях перемещение меньше пройденного пути.

• Если тело возвращается в исходную точку, перемещение равно нулю, а пройденный путь может быть сколь угодно большим.

Кинематический закон движения - это уравнения, описывающие зависимость координаты точки от времени

Эти три уравнения можно заменить одним уравнением радиус-вектора: .

Кинематический закон движения может быть задан: аналитическим уравнением, графически, или в виде таблицы.

§2. Скорость

Это векторная величина, которая характеризует быстроту и направление движения тела в данный момент времени.

Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r₀ (рис.).

В течение малого промежутка времени t точка пройдет путь s и получит элементарное (бесконечно малое) перемещение r.

• Вектор средней скорости <v> это отношение приращения r радиуса-вектора точки к промежутку времени t

Направление вектора средней скорости совпадает с направлением перемещения r.

• Мгновенная скорость – это векторная величина, равная первой производной радиуса-вектора движущейся точки по времени:

При Δt |, поэтому модуль мгновенной скорости

То есть, мгновенная скорость равна первой производной пути по времени. В каждый момент времени она направлена по касательной к траектории движения (рис. выше).

Модуль мгновенной скорости определяют как:

_где

З ная модуль , можно найти путь: ds

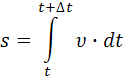
§3. Ускорение и его составляющие

Это векторная величина, характеризующая изменение скорости по величине и направлению.

• Средним ускорением неравномерного движения в интервале от t до t + t называется векторная величина, равная отношению изменения скорости v к интервалу вре­мени t

• Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет предел среднего ускорения:

Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.

Если скорость в каждый момент времени меняется и по величине, и по направлению (тело движется равноускоренно по криволинейной траектории), то вектор ускорения имеет 2 составляющих:

• 1 ) Тангенциальное (касательное) ускорение – направлено по касательной, характеризует изменение скорости по величине:

• 2) Нормальное (центростремительное) ускорение – направлено по нормали к траектории к центруее кривизны, характеризует изменение скорости по направлению:

• Полное ускорение равно геометрической сумме векторов:

• Модуль полного ускорения