Примеры решения задач

Задача 1

Лодка под парусом развила скорость . Считая, что после спуска паруса в стоячей воде сопротивление воды движению лодки можно считать пропорциональным квадрату скорости, показать, что полная работа сил трения лодки о воду будет равна начальной кинетической энергии лодки.

Решение.

Запишем второй закон Ньютона для движения лодки после спуска паруса:

, (3.4)

где  – масса лодки,  – постоянный коэффициент пропорциональ-ности.

Разделяем переменные и интегрируем с учетом того, что при , а в некоторый произвольный момент времени скорость лодки равна

.

Подставляя пределы интегрирования, получаем

,

и находим зависимость скорости лодки от времени

. (3.5)

Умножаем обе части уравнения (3.4) на элемент пути получаем в правой части элементарную работу силы сопротивления на отрезке пути

. (3.6)

Учитывая, что уравнение (3.6) перепишем как

и преобразуем к виду

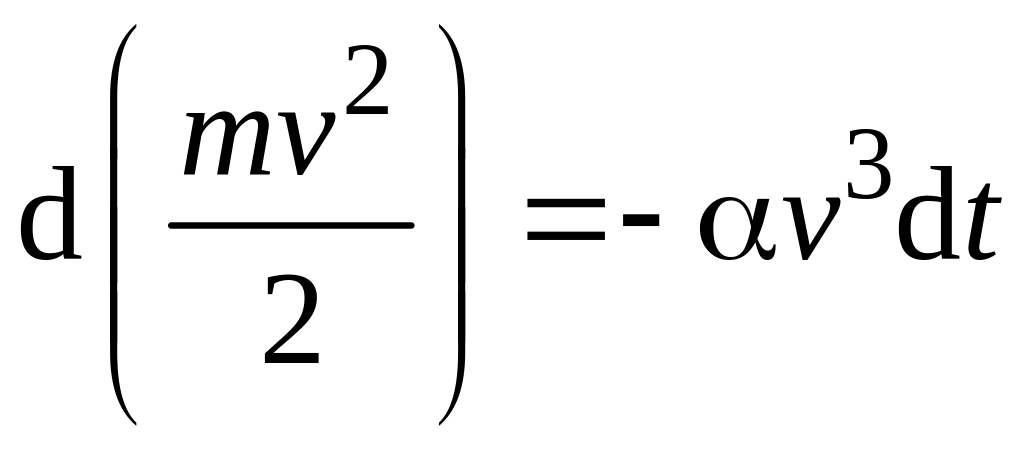. (3.7)

Левая часть уравнения (3.7) представляет собой изменение кинетической энергии лодки на отрезке пути

. (3.8)

Элементарная работа с использованием (3.5) будет равна

(3.9)

Интегрируя два последних уравнения (3.8) и (3.9) при условии, что при и при находим:

,

,

что и требовалось доказать.

Задача 2

Материальная точка находится в поле, потенциал которого зависит от расстояния до центра по закону , где и  – положительные постоянные. Найти положение равновесия точки, определить его устойчивость. Найти силу, действующую на точку, в зависимости от расстояния.

Решение.

Положения равновесия точки в потенциальном поле определяются экстремумами функции . Чтобы найти их, исследуем функцию на экстремум. Первая производная функции по расстоянию должна равняться нулю.

. , .

Для определения устойчивости равновесия проанализируем вторую производную функции

.

Для , т. е. в данной точке функция имеет минимум. Следовательно, это положение устойчивого равновесия точки.

Для , т. е. в данной точке функция имеет максимум. Следовательно, это положение неустойчивого равновесия точки.

Сила, действующая на тело в потенциальном поле, определяется как

.

Для определения модуля силы необходимо взять первую производную функции с отрицательным знаком:

.

Таким образом, при положение равновесия является устойчивым; при положение равновесия является неустойчивым; (рис. 3.1).

Рис. 3.1

Ответ: , положение равновесия устойчивое;  – неустойчивое; .

Задача 3

Частица массой налетает со скоростью на покоящуюся частицу массой ( < ) и после упругого нецентрального удара отклоняется на максимально возможный угол. Найти скорости частиц после соударения.

Решение.

Для замкнутой системы частиц выполняется закон сохранения энергии и импульса:

, (3.10)

(3.11)

где  – скорости частиц после соударения.

Введем для краткости величину . Тогда уравнения (3.10) и (3.11) перепишутся в виде:

(3.12)

(3.13)

Спроектируем уравнение (3.13) на оси координат:

(3.14)

(3.15)

Уравнения (3.12), (3.14), (3.15) связывают четыре неизвестных: Из уравнений (3.14) и (3.15) следует

, (3.16)

(3.17)

Возводя уравнения (3.16) и (3.17) в квадрат и складывая их, имеем

(3.18)

Из уравнения (3.12) получаем:

(3.19)

Подставляя выражение (3.19) в уравнение (3.18), находим уравнение, связывающее и

(3.20)

Вещественные корни для скорости возможны лишь для тех при которых дискриминант уравнения (3.20) неотрицателен, т. е.

(3.21)

Отсюда или . В этом случае знаку равенства соответствует максимальный угол отклонения, т. е.

.

Поскольку по условию задачи , то дискриминант уравнения (3.20) равен нулю, и решение для единственно:

.

Подставляя найденное выражение для в формулу (3.19), получаем

.

Тогда из уравнения (3.17) следует, что

.

Итак, в рассматриваемой системе координат

,

.

Ответ: , .

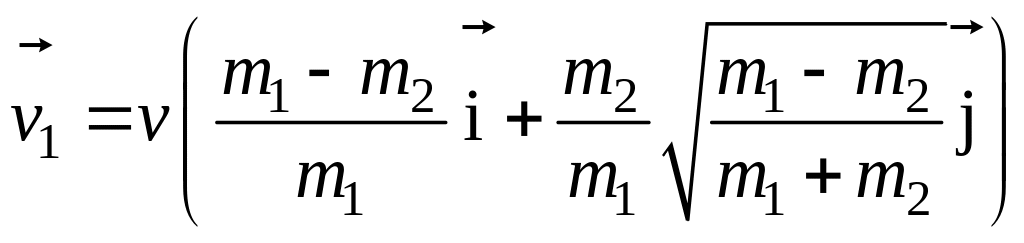Задача 4

Кусок однородного каната висит вертикально, причем нижний его конец доходит до горизонтального стола. Показать, что если верхний конец каната освободить, то в любой момент падения каната сила его давления на стол будет в три раза больше веса части каната, уже лежащей на столе.

Решение.

Дополнительное давление на стол (сверх веса части каната, уже лежащей на столе) вызвано потерей импульса падающими элементами каната при их ударе о стол. Пусть за элемент времени на стол падает элемент каната с массой где  – масса, приходящаяся на единицу длины каната, а  – элемент длины каната. Из второго закона Ньютона в общем виде сила, действующая со стороны этого элемента на стол, будет равна

где  – скорость, с которой элемент достигает стола. Но, как нетрудно заметить, где  – длина части каната, лежащей на столе. Отсюда Таким образом, полная сила, действующая на стол, будет равна

Задача 5

Прямоугольный клин с углом и массой поставлен на горизонтальную плоскость. Коэффициент трения клина о плоскость На клин положены тела А и В, массы которых соответственно и связанные гибкой нерастяжимой нитью, которая перекинута через блок С (рис. 3.2). Определить зависимость между скоростью клина и относительной (по отношению к клину) скоростью грузов А и В, если коэффициент трения грузов о боковые поверхности клина . В начале движения система находилась в покое. Массами блока и нити пренебречь.

Рис. 3.2

Решение.

Система неподвижна, а система координат подвижна (рис. 3.3).

Рис. 3.3

Применим теорему об изменении импульса движения, записанную в проекциях на ось

где

Интегрируя это равенство, имеем

Количество движения рассматриваемой системы состоит из количеств движения тел А и В, а также клина, т. е.

,

где  – абсолютные скорости движения грузов А и В соответственно,  – переносная скорость клина. Запишем последнее равенство в проекциях на ось (рис.3.4):

.

Рис. 3.4

Абсолютные скорости грузов А и В определим по теореме сложения скоростей: , или в проекциях на ось : . Так как переносное движение поступательное, то . В относительном движении проекция скоростей где  – скорость движения грузов относительно клина. Используя полученные формулы, получим

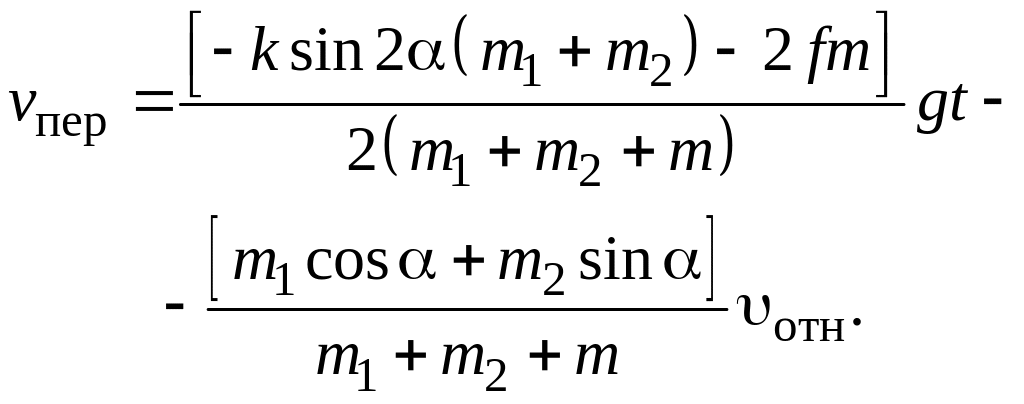
Поскольку , то клин движется в сторону, противоположную .

Задача 6

Шарик, закрепленный на невесомой нерастяжимой нити длиной отвели на от положения равновесия и толкнули в перпендикулярном направлении. В результате шарик начал вращение вокруг вертикальной оси. Через некоторое время скорость шарика стала Найти угол, который будет составлять нить с вертикалью. Сопротивлением воздуха пренебречь.

а б

Рис. 3.5

Решение.

Если шарик толкнуть в направлении, перпендикулярном плоскости, в которой находилась нить первоначально и после того, как ее отвели из положения равновесия, то он будет двигаться по спирали, располагающейся на сфере радиуса В частном случае, шарик будет двигаться по окружности радиуса со скоростью вокруг точки подвеса (рис. 3.5, а).

Для того чтобы найти угол, который составит нить с вертикалью, воспользуемся законами сохранения. Энергия при движении шарика сохраняется, поскольку сопротивления нет и растяжение нити не происходит (рис. 3.5, б):

(3.22)

Поскольку моменты силы тяжести и силы натяжения нити в данных условиях в проекции на вертикаль равны нулю, то запишем закон сохранения момента импульса:

. (3.23)

Из выражения (3.23) получаем соотношение между скоростями:

,

и подставляем его в закон сохранения энергии (3.22):

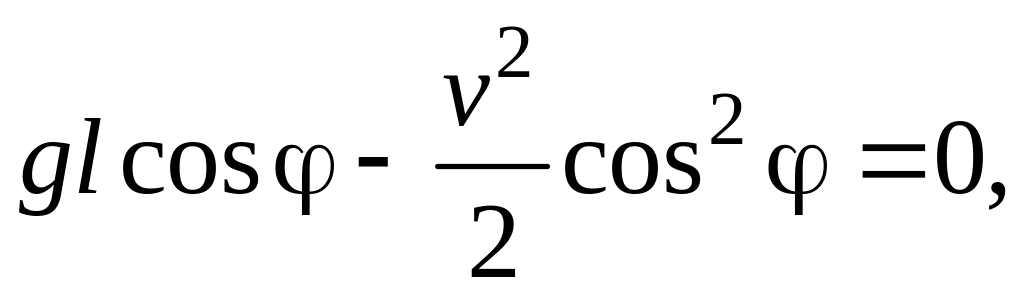
(3.24)

Для того чтобы удовлетворялось выражение (3.24), возможны два значения углов, на которых может вращаться шарик. В первом случае , и в этом случае скорость шарика не должна изменяться с течением времени. Во втором случае

. (3.25)

Из выражения (3.25) находим искомый угол.

Ответ: .

Задача 7

В ускорителях на встречных пучках исследуемые частицы, разогнанные до одинаковых релятивистских энергий, движутся навстречу друг другу и реагируют при столкновении. Суммарный импульс таких частиц, а с ним и кинетическая энергия, связанная с движением центра масс, равны нулю как до, так и после столкновения. Поэтому вся кинетическая энергия частиц может быть использована для получения исследуемой реакции. Исследовать случай: два протона с одной и той же кинетической энергией = 10 ГэВ движутся навстречу друг другу. До какой кинетической энергии надо ускорить только один протон, оставляя второй (мишень) неподвижным, чтобы эта энергия была эквивалентна (в смысле возможности превращения сталкивающихся частиц)?

Решение.

Рассмотрим сначала движение частицы в системе центра масс. В этой системе протоны движутся навстречу друг другу с одинаковыми скоростями. Обозначим через полную энергию каждого из них в этой системе. Поскольку суммарный импульс протонов равен нулю, они вместе могут рассматриваться как одна частица (как до, так и после столкновения) с массой покоя определяемой соотношением

Перейдем теперь в лабораторную систему отсчета, в которой один из протонов (мишень) покоится, а другой движется. Такой переход, очевидно, никак не скажется на внутренних превращениях, которые могут претерпевать частицы. Обозначим через полную энергию движущегося протона, а через  – его импульс в лабораторной системе отсчета. Задача состоит в том, чтобы найти связь между энергиями и Суммарный импульс обоих протонов в той же системе отсчета будет , а энергия В релятивистской механике энергия связана с импульсом соотношением:

,

откуда

С другой стороны, если написать соотношение между энергией и импульсом только для движущегося протона, то получится

, откуда .

Сравнивая оба выражения для , получим

.

Чтобы получить кинематическую энергию протона в лабораторной системе, надо вычесть отсюда энергию покоя . Это дает

.

Если, как в разбираемом случае, то

.

Для протона = 0,937 ГэВ, поэтому 250 ГэВ.

Ответ: 250 ГэВ.

Задача 8

В ракете продукты сгорания (газы) выбрасываются со скоростью  = 3 км/с (относительно ракеты). Найти отношение ее кинетической энергии к кинетической энергии продуктов сгорания в момент достижения ракетой скорости  = 12 км/с.

Решение.

Приращение скорости ракеты связано с изменением ее массы соотношением причем где  – масса выброшенных газов. Приращение кинетической энергии газов:

Подставив сюда и воспользовавшись формулой Циолковского , получим

,

или после интегрирования в пределах от 0 до

,

где для краткости введено обозначение .

Кинетическая энергия ракеты

.

В результате находим

.

Ответ: При %.

Задача 9

При столкновении протонов высоких энергий могут образовываться антипротоны согласно реакции

Какой минимальной (пороговой) кинетической энергией должен обладать протон, чтобы при его столкновении с покоящимся протоном была возможна такая реакция?

Решение.

Условие, при котором рассматриваемая реакция происходит с минимальной затратой энергии, легко найти, рассмотрев процесс в системе центра масс. Затраченная энергия будет минимальна, если в этой системе все четыре образовавшиеся частицы покоятся. В лабораторной системе они будут двигаться с одинаковыми скоростями, как если бы образовалась одна частица с массой покоя или энергией . Эту энергию удобно обозначить Таким образом, , где  – энергия протона. Полная энергия движущегося протона (с импульсом p) до реакции будет . Поскольку при столкновении импульс сохраняется, полная энергия образовавшихся частиц представится выражением . Из закона сохранения энергии следует

,

откуда

.

Чтобы найти исходную кинетическую энергию протона, надо из полной его энергии вычесть энергию покоя. Это дает

.

В рассматриваемом случае , так что .

Ответ: .

Задача 10

Человек на аттракционе «гигантские шаги» движется по замкнутой траектории таким образом, что достигаемая им высота относительно положения равновесия меняется в пределах от до . Определить максимальную и минимальную скорости человека при таком движении, если длина веревки, на которой он удерживается, равна

Решение.

Рис. 3.6

На основании закона сохранения энергии Момент силы тяжести относительно точки подвеса не имеет вертикальной составляющей. Момент силы натяжения веревки равен нулю. Поэтому при движении человека вертикальная составляющая его момента импульса остается неизменной. В положении, где высота максимальна или минимальна, проекция скорости человека горизонтальна, а момент

импульса равен , где  – расстояние до вертикальной оси, вокруг которой вращается человек. Значит, в этих положениях величина одна и та же. В момент, когда высота максимальна или минимальна, опишем в вертикальной плоскости окружность с центром в точке подвеса О, проходящую через точку нахождения человека (рис. 3.6). По известной геометрической теореме , или . Поэтому в положениях, где максимальна и минимальна,

Запишем найденные соотношения для этих положений, имея в виду, что максимум соответствует минимум и наоборот. Получим:

Решая эти уравнения, получим:

, (3.26)

. (3.27)

При этом учтено, что в реальных условиях так что величина (3.26) действительно максимальна, а (3.27) – действительно минимальна. Если и пренебрежимо малы по сравнению с то

Ответ: , .