2. Законы динамики

_____________________________________________________________________________________________________________________________________________________________________________________________________________________________

Краткая теория и методические указания

Первый закон Ньютона утверждает, что существуют такие системы отсчета, в которых выполняется закон инерции: тело движется равномерно и прямолинейно либо покоится, если на него не действуют внешние силы или действие этих сил скомпенсировано. В дальнейшем будем предполагать, что все описания движения ведутся в инерциальной системе отсчета, если специально не оговорено обратное. Поэтому, если тело движется с ускорением, значит на него действует некая результирующая сила.

Сила – это мера механического действия на данное материальное тело других тел как при непосредственном контакте, так и через посредство создаваемых телами полей (поле тяготения, электрическое поле и т. д.). Она характеризуется численным значением, направлением и точкой приложения, т.е. является вектором.

В механике наиболее характерны следующие типы задач:

I – определение силы по характеру вызываемого ею движения;

II – нахождение закона движения по заданным силам.

Согласно второму закону Ньютона, если масса тела не изменяется, в инерциальной системе выполняется равенство где  –результирующая всех сил, действующих на тело;  – масса тела;  – его ускорение. Если положение тела в пространстве характеризуется радиусом-вектором то второй закон Ньютона примет вид

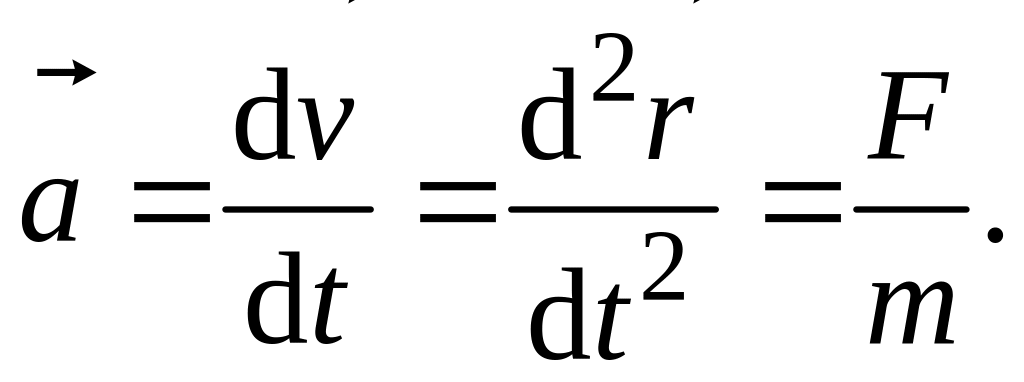(2.1)

Равенство (2.1) называется уравнением движения. С его использованием решаются задачи обоих типов. При решении задач типа I нужно использовать тот факт, что ускорение (или его проекции) есть вторая производная от радиуса-вектора (или соответствующих ему координат) по времени:

.

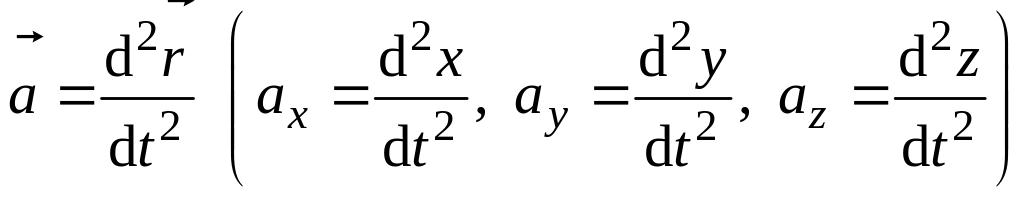При решении задач типа II равенство (2.1) нужно рассматривать как дифференциальное уравнение второго порядка для нахождения (или проекций ). При решении дифференциальных уравнений второго порядка появляются две произвольные постоянные (константы интегрирования). Их находят из начальных условий (координаты и скорости в начальный момент времени). Заметим, что при определении произвольных постоянных не обязательно пользоваться именно начальными условиями. Например, вместо начальной скорости могут быть заданы координаты точки в другой (неначальный) момент времени или другие физические характеристики, в которые входят произвольные постоянные, например, энергия тела, если выполняется закон сохранения энергии, и т. п.

Рассматривая задачи I и II типов, предполагали, что никаких препятствий движению тела нет, и оно определяется лишь действующей силой и начальными условиями. Однако во многих случаях тело находится в таких условиях, что в некоторых направлениях движение оказывается невозможным. Это взаимодействие с телом можно описать как результат действия некоторой силы, называемой реакцией связи (сила реакции опоры или подвеса). Реакции связей вводятся в уравнение движения на основании третьего закона Ньютона и складываются с силами, действующими на тело. Обычно в задачах предполагаются идеальные связи: поверхности, с которыми соприкасается тело, считаются абсолютно твердыми; нити – невесомыми и нерастяжимыми; стержни –несгибаемыми и невесомыми и т. д.

При соприкосновении данного тела с другими телами кроме указанного ограничения возможности движения часто оказывается заметным трение, которое тормозит движение. Сила трения направлена противоположно направлению движения тела (например, сила трения скольжения) или противоположно результирующей силе, стремящейся вывести тело из состояния покоя (сила трения покоя). Во многих случаях трение о поверхность считает пропорциональным силе нормальной реакции опоры. Для нахождения силы нормальной реакции опоры составляется уравнение на основании того, что вдоль координатной оси, перпендикулярной направлению скорости прямолинейного движения тела, ускорение отсутствует, и поэтому сумма проекций сил на эту ось равна нулю. В некоторых случаях, например, при движении тела в среде (в воде, масле и т. д.) сила трения зависит от скорости движения тела. Сила трения также вводится в уравнения движения Ньютона.

Задачи по динамике движения по окружности решаются так же, как и задачи по динамике прямолинейного движения, при этом прямоугольную систему координат рационально выбирать так, чтобы одна из осей (например, ) была направлена из точки, в которой находится тело, по радиусу к центру окружности. Тогда и при равномерном, и при неравномерном движении по окружности проекция ускорения на эту ось равна модулю центростремительного (нормального) ускорения.

Во многих задачах механики весьма сложные объекты можно считать материальными точками. Однако, если нужно исследовать законы качения, например, колеса, модель точки неприменима, и следует вводить модель твердого тела. Обычно допустимость точечной модели для движущегося объекта очевидна из условия задачи и специально в ней не оговаривается.

Создав основы классической механики, Ньютон решил задачу типа I: по закону движения планет (законы Кеплера) нашел гравитационную силу, действующую между Солнцем и Землей:

где  – масса планеты;  – расстояние ее центра от центра Солнца;  – радиус-вектор планеты (при начале координат в центре Солнца). Оказалось, что этот закон верен для любой пары тел, если рассматривать расстояния между телами так, что тела можно считать точечными. Поэтому закон назван законом всемирного тяготения и может быть записан в виде зависимости силы от расстояния между телами: , где  –  гравитационная постоянная; ; ,  – массы взаимодействующих (точечных) тел;  – расстояние между ними.

Простым расчетом можно показать, что два однородных шара притягиваются друг к другу так, как если бы масса каждого шара была сосредоточена в его центре. В частности, взаимодействие между точечным телом, находящимся на поверхности Земли, и Землей можно описывать как взаимодействие между точкой и центром Земли, если считать, что вся ее масса сосредоточена в центре. Поэтому гравитационная сила, действующая на тело (точку), находящееся на поверхности Земли: , где  – масса Земли;  – масса тела;  – радиус Земли (расстояние до центра Земли), который можно считать приблизительно постоянным. Поэтому (ускорение поля тяжести = 9,81 м/с²). Поскольку сила направлена к центру Земли (а на поверхности Земли это направление соответствует направлению по вертикали), то вектор силы , где  – ускорение, направленное по вертикали вниз.

Если проводить более точные исследования силы притяжения к Земле, нужно учитывать то обстоятельство, что значения неодинаковы в разных точках Земли, поскольку ее форма не шар, а геоид, сплюснутый у полюсов.

Есть и другой фактор, влияющий на силу притяжения тела к Земле: вращение земного шара. Если тело находится не на полюсе, то на него действует центробежная сила, возникающая потому, что тело оказывается во вращающейся системе. Центробежная сила (  – угловая скорость точки;  – расстояние ее от оси вращения) и направлена от оси. Если тело находится на широте , , так что . Поэтому сила, действующая на точку , равна Хотя , силой не всегда можно пренебрегать.

Весом тела называется сила, с которой тело действует на опору или подвес. Очевидно, что определять вес следует с помощью пружинных весов, так как рычажные весы позволяют сравнивать лишь массы тел.

Можно показать, что внутри Земли на расстоянии от ее центра где – масса вещества Земли, ограниченного сферой радиусом Если плотность вещества Земли обозначить через , то , так что

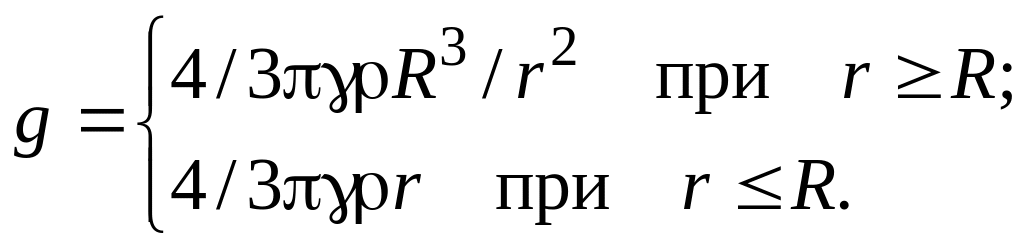
При исследовании движения планет вокруг Солнца само Солнце можно считать неподвижным. Выбрав начало координат в центре Солнца, видим, что сила, действующая на планету, центральна. Следовательно, момент импульса планеты относительно начала координат сохраняется.

Так как гравитационная сила не зависит от времени, то, если не действуют другие силы, зависящие от времени, или сила трения, выполняется закон сохранения механической энергии.

Законами сохранения энергии и момента импульса удобно пользоваться при решении некоторых задач о движении точки в центральном поле.