Пример. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и проинтегрировав его почленно.
Решение.
Ответ:
К заданиям 431-440.
Пример. Найти
четыре первых, отличных от нуля члена
разложения в степенной ряд решения
y=y(x)
дифференциального уравнения
.
Решение. В тех
случаях, когда для уравнения
требуется решить задачу Коши при
начальном условии y(x0)=y0,
решение можно искать с помощью ряда
Тейлора:
где
,
а дальнейшие производные находят
последовательным дифференцированием
исходного уравнения и подстановкой в
результат дифференцирования вместо
,
… значений
и всех остальных найденных последующих
производных.
Из уравнения
и начального условия находим
Дифференцируя
данное уравнение, последовательно
получаем
,
.Полагая
,
и используя
находим
Аналогично, используя значения
,
находим
Искомое решение имеет вид Ответ:
К заданиям 441-450.
Пример. Разложите
функцию
в ряд Фурье в интервале
.
Решение. Эта функция – кусочно - монотонная и ограниченная. Следовательно, она допускает разложение в ряд Фурье.
Определим ее коэффициенты Фурье:
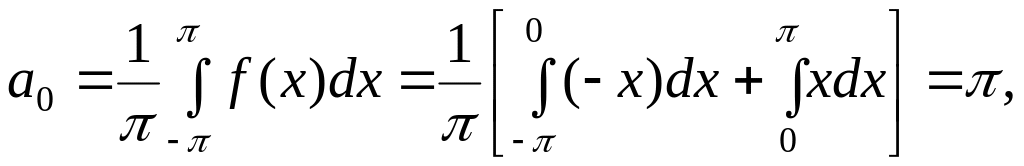
при k
– четном,
при
k
– нечетном.
Таким образом,
получаем ряд
Этот ряд сходится во всех точках, и его сумма равна данной функции.
Ответ:
Задания на контрольные работы. Контрольная работа №4
Задание 1. Вычислить двойной интеграл по области, ограниченной линиями
№331. |
|
D: y=x2 , y=0, x=1 |
№332. |
|
D: y=x2 , y=0, x=2 |
№333. |
|
D: y=4x2 , y=0, x=1 |
№334. |
|
D: y=1+x2 , y=1, x=2 |
№335. |
|
D: y=x2 , y=1, x=3 |
№336. |
|
D: y=x2 , y=0, x=1, x=2 |
№337. |
|
D: y=1+ x3 , y=1, x=4 |
№338. |
|
D: y=x3 , y=0, x=2 |
№339. |
|
D: y=x2 , y=2, x=3 |
№340. |
|
D: y=x3 , y=0, x=3 |
Задание 2. Вычислите с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а>0)
№341. |
(x2 + y2)3=4x2y2
|
№342. |
(x2 + y2)2=25(4x2 + y2)
|
№343. |
(x2 + y2)3=9(4x2 + y2)
|
№344. |
(x2 + y2)2=4(3x2 + 2y2)
|
№345. |
x4 =16(3x2-y2)
|
№346. |
x6=9(x4 - y4)
|
№347. |
x4 =a(x2 - 3y2)
|
№348. |
y6=a2 (y4 - x4)
|
№349. |
(x2 + y2)2=a2(2x2 + 3y2)
|
№350. |
y6=a2 (x2 + y2) (3y2 + x2)
|
Задание 3. Вычислите с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость ХОY.
№351 |
z=0,
z=x,
y=0,
y=3,
x=
|
№352. |
z=0, z=16–y2, x2+y2 = 16 |
№353. |
z=0, z=25-x-y, x2+y2 = 25 |
№354. |
z=0, z=y2, x2+y2=4 |
№355. |
z=0, y+z=3, x2+y2=9 |
№356. |
z=0, z=4y2, 2x – y =0, x+y = 9 |
№357. |
z=0, z=x2+y2, x2+y2 = 9 |
№358. |
z=0, z=1-y2, x=4y2 , x=4y2 +1 |
№359. |
z=0, z=4-x2, y=0 , x=4-x |
№360. |
z=0,
z=9 |
,
x=0, x+y=9
Задание 4. Вычислите криволинейный интеграл
№361. |
|
вдоль дуги L окружности x=5cost, y=5sint, обходя ее против хода часовой стрелки от точки А(5;0) до точки В(0;5). Сделать чертеж.
|
№362. |
|
вдоль ломаной L=ОАВ, где О(0;0), А(-1;1) до точки В(4;5). Сделать чертеж.
|
№363. |
|
вдоль границы L треугольника АВС, обходя ее против хода часовой стрелки, если А(2;0), В(2;2), С(0;2). Сделать чертеж.
|
№364. |
|
вдоль дуги L параболы y= x2 от точки А(-1;1) до точки В(1;1). Сделать чертеж.
|
№365. |
|
вдоль верхней
половины L
эллипса x=2cost,
y=3sint
(0<t<
|
№366. |
|
вдоль ломаной L=АВC, где A(1;2), B(1;5), C(3;5). Сделать чертеж.
|
№367. |
|
вдоль дуги L кривой y=e-x от точки А(0;1) до точки В(-1;e). Сделать чертеж.
|
№368. |
|
вдоль отрезка L=АВ прямой от точки А(-1;2) до точки В(-2;4). Сделать чертеж.
|
№369. |
|
вдоль дуги L параболы y=2x2 от точки O(0;0) до точки А(2;8). Сделать чертеж.
|
№370. |
|
вдоль дуги L кривой y=lnx от точки A(1;0) до точки B(e;1). Сделать чертеж. |
).
Сделать чертеж.
Задание 5.
Даны векторное поле
и плоскость Ax+By+Cz+D=0
(p),
которая совместно с координатными
плоскостями образует пирамиду V.
Пусть - основание пирамиды, принадлежащее плоскости (р); - контур, ограничивающий ;
n –нормаль к , направленная вне пирамиды V.
Требуется вычислить:
1) поток векторного поля F через поверхность в направлении нормали n;
2) циркуляцию векторного поля F по замкнутому контуру и ограниченной им замкнутой поверхности с нормалью n;
3) поток векторного поля F через полную поверхность пирамиды V в направлении внешней нормали к ее поверхности, применив теорему Остроградского. Сделать чертеж
№371. |
|
№372. |
|
№373. |
|
№374. |
|
№375. |
|
№376. |
|
№377. |
|
№378. |
|
№379. |
|
№380. |
|
x+y+z-2=0
2x-y+2z-2=0
x+y+z-4=0
-x+2y+2z-4=0
2x-3y+2z-6=0
3x+2y+3z-6=0
-x+2y+z-4=0
x-y+2z-4=0
x+y+3z-3=0
-x+y+2z-4=0
Задание 6. Проверить является ли векторное поле потенциальным и соленоидальным. В случае потенциальности поля найти его потенциал.
№381. |
|
№382. |
|
№383. |
|
№384. |
|
№385. |
|
№386. |
|
№387. |
|
№388. |
|
№389. |
|
№390. |
|
Контрольная работа №5
Задание 1. Исследовать сходимость числового ряда
№391. |
|
№392. |
|
№393. |
|
№394. |
|
№395. |
|
№396. |
|
№397. |
|
№398. |
|
№399. |
|
№400. |
|
Задание 2.
Найти интервал сходимости степенного
ряда
№401. |
|
№402. |
|
№403. |
|
№404. |
|
№405. |
|
№406. |
|
№407. |
|
№408. |
|
№409. |
|
№410. |
|
Задание 3. Вычислить значение функции с точностью до 0,001, разложив ее в степенной ряд.
№411. |
|
№412. |
|
№413. |
|
№414. |
|
№415. |
|
№416. |
|
№417. |
|
№418. |
|
№419. |
|
№420. |
|
при
при
при
при
при
при
при
при
при
при
Задание 4.
Вычислить определенный интеграл
с точностью до 0,001, разложив подынтегральную
функцию в степенной ряд и проинтегрировав
его почленно.
№421. |
|
№422. |
|
№423. |
|
№424. |
|
№425. |
|
№426. |
при b=0,6 |
№427. |
|
№428. |
|
№429. |
|
№430. |
|
при b=1,1.
при b=1,1.
при b=0,6.
при b=0,6.
при b=0,6
при b=0,6.
при b=1,1.
при b=0.6.
при b=0,6
Задание 5.
Найти три первых, отличных от нуля члена
разложения в степенной ряд решения
y=y(x)
дифференциального уравнения
,
удовлетворяющего начальному условию
.
№431. |
|
№432. |
|
№433. |
|
№434. |
|
№435. |
|
№436. |
|
№437. |
|
№438. |
|
№439. |
|
№440. |
|
Задание 6
Разложите данную функцию
в ряд Фурье в интервале (a;b)..
№441. |
|
№442. |
|
№443. |
|
№444. |
|
№445. |
|
№446. |
|
№447. |
|
№448. |
|
№449. |
|
№450. |
|
,
в интервале
в интервале
в интервале
в интервале
в интервале
в интервале
в интервале
в интервале
в интервале
в интервале