3. Закодировать методом «желательных соседств» состояния автомата и получить соответствующую минимальную систему днф.

	0	1
1	2,1	1,0
2	4,0	3,1
3	1,0	5,1
4	5,1	1,0
5	3,1	4,0

Решение.

Введем три фиктивных состояния , и , чтобы довести число состояний до . Значения , где - число столбцов таблицы переходов, в которых строки и имеют одинаковые элементы, т.е. число значений переменной , при которых .

Таблица переходов:

	0	1
1	2	1
2	4	3
3	1	5
4	5	1
5	3	4

А , где - число состояний автомата, - число пар вида , причем и , а входные символы и имеют соседние коды, удобно задать в виде таблицы:

1	0	1	2	0	0	0
	0	0	0	0	0	0
		2	0	0	0	0
			0	0	0	0
				0	0	0
					0	0
						0

где строки и столбцы соответствуют состояниям автомата.

На первом шаге получаем четыре одномерных гиперкуба. Максимальное значение имеет вес и . Поэтому в первую очередь вводим ребра между вершинами и , и . Затем вводим остальные ребра.

Сначала строится один двухмерный гиперкуб, для которого выбираются два ребра с максимальной суммой весов. Затем точно также собирается второй гиперкуб.

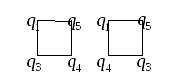
Вершины , и здесь не участвуют , так как все инцидентные им ребра имеют нулевой вес и сумма их весов заведомо не максимальна. Максимальной суммой весов обладает второй вариант.

Окончательным будет гиперкуб:

Теперь можем составить таблицу кодирования состояний:

	0	0	0
	1	0	0
	0	1	1
	0	0	1
	0	1	0

Булев автомат, соответствующий данному варианту кодирования, представим тремя картами Карно, которые задают не полностью определенные функции , и и строкам которых соответствуют состояния заданного автомата

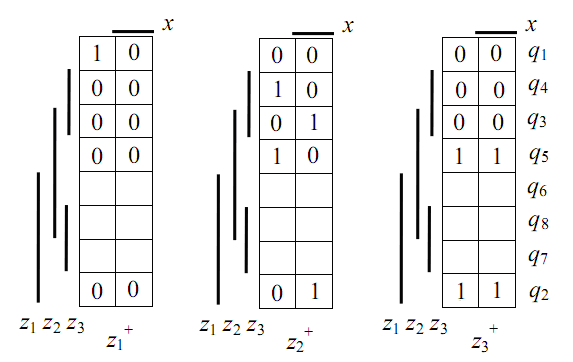
Минимизированная система булевых функций, описывающая заданное поведение, представляется следующими матрицами:

Х	Z1	Z2	Z3			Z1+	Z2+	Z3+	Y
0	0	0	0			1	0	0	1
1	1	0	0			0	1	1	1
1	0	1	1			0	1	0	1
0	0	0	1			0	1	0	1
0	0	1	0			0	1	1	1
-	1	0	0			0	0	1	0
-	0	1	0			0	0	1	0