2. Поверхности вращения

Поверхностью вращения общего вида называют поверхность, которая образуется в результате вращения произвольной кривой (образующей) вокруг неподвижной оси (рис. 11).

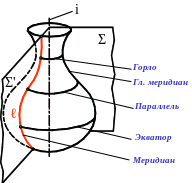
Рис. 11

Каждая точка образующей ℓ при вращении вокруг оси i описывает окружность с центром на оси вращения. Эти окружности называются параллелями, наибольшая параллель – экватор, наименьшая – горло. Плоскость Σ′ проходит через ось вращения и называется меридиональной плоскостью, а линия ее пересечения с поверхностью вращения (образующая ℓ) – меридианом. Если плоскость Σ, пересекающая поверхность вращения, параллельна какой-либо плоскости проекций, то линия ее пересечения с поверхностью называется главным меридианом.

Из всего многообразия поверхностей вращения в настоящих методических указаниях рассматриваются конус, цилиндр, сфера, тор:

- конус вращения образуется в результате вращения образующей вокруг неподвижной оси, при этом все образующие имеют одну общую точку - вершину S (рис. 12);

- цилиндр вращения образуется в результате вращения образующей вокруг неподвижной оси, при этом все образующие параллельны между собой (рис. 13);

- сфера образуется в результате вращения полуокружности вокруг своего диаметра (рис. 14);

- тор образуется при вращении окружности вокруг оси, не проходящей через ее центр (рис. 15).

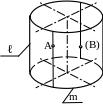
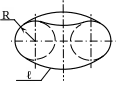
Рис. 12 Рис. 13

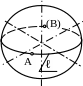
Рис. 14 Рис. 15

2.1. Пример построения проекций точек на поверхностях вращения

S₂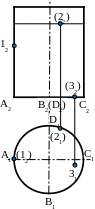

Построение точек на поверхности конуса показано на рис. 16. Проекции точки 2 для примера построены с помощью секущей плоскости и с помощью образующей. Построение точек на поверхности цилиндра показано на рис. 17.

2₂

1₂

А₂

С₂

В₂(D₂)

D₁

С₁

S₁

А₁

1₁

2₁

В₁

Рис.16 Рис.17

Построение точек на поверхности сферы показано на рис. 18;

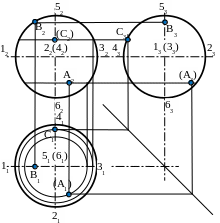
Рис. 18

Построение точек на поверхности тора показано на рис. 19. Построение выполнено с помощью образующих (образующими тора в данной задаче являются полуокружности, имеющие общий центр).

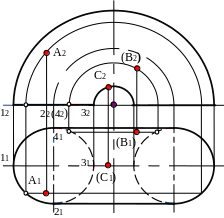
Рис. 19

2.2. Построение вырезов и линии на поверхностях вращения

Для того чтобы построить недостающие проекции вырезов или линий на поверхностях вращения, необходимо:

1. Линию разбить на некоторое количество точек.

2. Построить недостающую проекцию этих точек.

3. Плавной линией соединить полученные проекции точек.

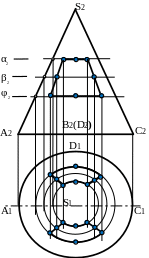
На рис. 20 показан пример построения выреза в конусе с помощью секущих плоскостей (α, β, φ).

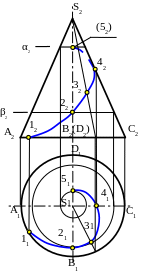
На рис. 21 показан пример построения горизонтальной проекции линии на поверхности конуса. Проекции точек 2 и 5 построены с помощью секущих плоскостей (α, β), точка 3 - с помощью образующей.

B1

Рис. 20 Рис. 21

На рис. 22 показан пример построения точек на поверхности наклонного цилиндра. Для построения используются образующие, которые в цилиндре параллельны между собой и параллельны оси цилиндра.

(3₂)

1₂

2₂

A₂

C₂

B₂(D₂)

D₁

A₁

C₁

(3₂)

2₂

1₁

B₁

Рис. 22

На рис. 23 показан пример построения точек на поверхности наклонного конуса. Для построения используются образующие, которые в конусе имеют общую точку – это его вершина.

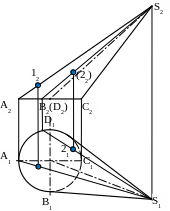
1₁

Рис. 23