Лекция 4 поверхности

Определение: Поверхность – это совокупность всех последовательных положений некоторой, перемещающейся в пространстве линии. Поверхности делятся на группы:

- линейчатые поверхности,

- поверхности вращения,

- многогранники,

- винтовые поверхности.

Поверхность получается в результате движения образующей вдоль направляющей. Совокупность образующих и направляющих называется каркасом поверхности (рис. 1).

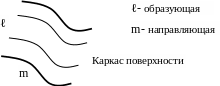
Рис. 1

Из всего многообразия поверхностей в настоящем методическом указании рассматриваются только поверхности вращения и многогранники, т.к. именно они представляют наибольший практический интерес для выполнения графических и практических заданий для студентов.

Точка и линия на поверхности

1. Точка принадлежит поверхности, если она принадлежит линии этой поверхности.

2. Линия принадлежит поверхности, если все ее точки принадлежат этой поверхности.

Последовательность решения задач для построения проекций точек

на поверхности

1. Через заданную проекцию точки провести образующую (или секущую плоскость).

2. Построить недостающую проекцию этой образующей (или секущей плоскости).

3. Спроецировать на построенную проекцию образующей (или секущей плоскости) исходную точку.

Приведенная выше последовательность проецирования точек может быть применена к любой поверхности вращении или к многограннику.

1. МНОГОГРАННИКИ

Многогранники – это пространственные замкнутые фигуры, ограниченные плоскими многоугольниками. Плоские многоугольники, ограничивающие боковые стороны многогранника, называются гранями, а линии пересечения граней – ребрами.

Многогранники называются метрически правильными, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр (рис.2).

Рис. 2

Из всего многообразия многогранников наибольший практический интерес представляют призмы и пирамиды.

1.1 Призма

Призма - многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани —параллелограммами, имеющими общие стороны с этими многоугольниками  (рис. 3).

.

Рис. 3

Пример построения проекций точек на поверхности прямой призмы

Призма называется прямой, если ее ребра перпендикулярны основанию.

Характерной особенностью построения проекций точек на прямой призме является то, что все ее боковые грани проецируются на горизонтальную плоскость в виде прямых линий.

Даны проекции точек 1₂, 2₂, 3₁. На рис. 4 построены недостающие проекции заданных точек.

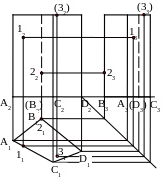
Рис. 4

На рис. 5 показано построение фронтальной и горизонтальной проекций точек на наклонной призме с помощью образующих (образующие призмы параллельны между собой).

Рис. 5