Линейные дешифраторы

В линейных дешифраторах каждое уравнение системы (14.1) реализуется отдельным ЛЭ. В качестве примера рассмотрим линейный дешифратор 3-8, у которого функции выходов имеют вид:

Эти уравнения могут быть реализованы с помощью восьми трехвходовых элементов И, как показано на рис.14.2.

У такого дешифратора активным уровнем является высокий уровень. Именно такой уровень будет на одном из выходов, определяемом значением числа, в то время как на всех остальных выходах будут напряжения низкого уровня. Линейный дешифратор может быть реализован на ЛЭ ИЛИ-НЕ. Для этого следует преобразовать уравнения (14.1), воспользовавшись, например, правилами де Моргана. Для дешифратора 3-8 эти преобразования дадут:

Достоинством линейного дешифратора является его высокое быстродействие, определяемое временем задержки tздр.р.ср. одного ЛЭ. Недостаток - увеличение числа входов каждого ЛЭ с ростом разрядности.

Дешифратор чаще всего подключается к выходным разрядам счетчика или регистра. При этом, как это видно из рис. 14.2, каждый разряд источникасигнала нагружается на n²=2^m/2 входов ЛЭ дешифратора, что может существенно повлиять на помехоустойчивость. Поэтому входы дешифратора обычно делаются единичными с последующим размножением внутри микросхемы, как показано на рис. 14.3 для дешифратора 2-4. Значок ▷ внутри УГО означает, что используются инверторы с умощенным выходом. Если использовать не двухвходовые, а трехвходовые ЛЭ И, то третьи входы можно объединить и использовать в качестве входа разрешения. Такие дешифраторы называются стробируемыми. Выполненный таким образом стробирующий вход обладает тем достоинством, что не вносит дополнительной задержки в дешифратор, т.е. не влияет на его быстродействие. Недостаток - требуется увеличение числа входов ЛЭ на 1.

Работа стробируемых дешифраторов описывается логическими уравнениями, подобными уравнениям (14.1), но содержащими дополнительно сигнал разрешения Е:

Для увеличения разрядности дешифраторов можно использовать их каскадное соединение. На рис. 14.4 показан дешифратор на 4 входа и 16 выходов, полученный каскадным соединением четырех стробируемых дешифраторов «2-4». Дешифрируемый двоичный код возбуждает один из выходов дешифратора. Если А ≤ 3, то работает DC1 (у0 = 1, y1 = у2 = у3 = 0 ). При 3 ≤ А ≤ 7 работает DC2 (y₁ = 1, у₀ = у₂ = у₃ = 0). При 7 ≤ А ≤ 11 работает DC3 (у₂ = 1, у₀ = у₁, = у₃ = 0), а при А > 11 - дешифратор DC4 (y₃ = 1, y₀ = y₁ = y₂ = 0).

(14.2)

В сериях ТТЛ и ТТЛШ дешифраторы обычно имеют инверсные выходы, поскольку их реализация осуществляется на элементах И-НЕ, являющихся наиболее технологичными в этих сериях. В КМДП-сериях, выполненных на инверторах, предпочтение имеют устройства, выполненные на элементах ИЛИ-НЕ, и дешифраторы чаще имеют прямые выходы.

Многоступенчатые дешифраторы

Если каскадное соединение дешифраторов не обеспечивает получение нужной разрядности дешифрируемого адресного кода, то дешифраторы строятся по многоступенчатой схеме. При этом различают прямоугольные и пирамидальные дешифраторы. Рассмотрим пример синтеза прямоугольного дешифратора 4-16, уравнения выходов которого имеют вид:

Таким образом, разряды адреса представлены двумя группами (g₀…g₃ и h₀…h₃), каждая из которых независимо от другой может расшифровываться своим линейным дешифратором 2-4. Эти дешифраторы образуют первую ступень дешифратора 4- 16. Вторую ступень образует матрица из двухвходовых элементов И , реализующих функции gi hj (рис. 14.5).

Делить разряды адреса между дешифраторами первой ступени нужно по возможности поровну: чем ближе прямоугольная матрица к квадратной, тем при том же числе элементов И меньше сумма его строк и столбцов, т.е. меньше число выходов дешифраторов первой ступени. В качестве входа Е всего двухступенчатого дешифратора удобно использовать разрешающий вход одного из дешифраторов первой ступени. При этом запираются все строки или все

с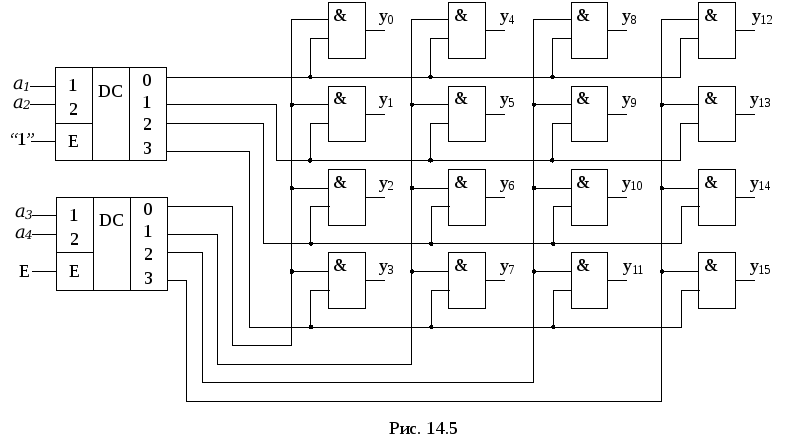толбцы.

Число ступеней может быть больше двух. Но следует иметь в виду, что с ростом числа ступеней увеличивается время задержки дешифратора.

Прямоугольные дешифраторы широко применяются в БИС памяти. При проектировании же блоков из готовых микросхем, когда затраты оборудования оцениваются не числом элементов, а числом корпусов, даже большие дешифраторы удобно строить по каскадному принципу.