
- •1. Счетчики Основные параметры и классификация
- •4. Счётчики с параллельным переносом
- •5. Счетчики с параллельным занесением информации
- •7. Счетчики с произвольным модулем счета и управляемым сбросом
- •8. Генераторы чисел на основе счетчиков
- •9. РегистрыНазначение и классификация
- •11. Параллельно-последовательные регистры
- •12. Использование сдвиговых регистров в качестве счётчиков
- •13. Кольцевой счётчик
- •Счётчик Джонсона
- •14. Одновибраторы
- •14_2 Мультивибраторы
- •15. Формирователи коротких импульсов
- •16. Антидребезговые формирователи импульсов
- •Линейные дешифраторы
- •Многоступенчатые дешифраторы
- •Демультиплексоры
- •19. Мультиплексоры
- •Переключательная функция и синтез мультиплексоров
- •Другие области применения мультиплексоров
- •20. Мультиплексор как генератор логических функций
- •21. Сумматоры
- •Одноразрядные двоичные сумматоры
- •22. Полный одноразрядный сумматор
- •23. Многоразрядные последовательные сумматоры
- •24. Многоразрядные параллельные сумматоры
- •25 Двоично-десятичные сумматоры
- •27. Схема сравнения на равенство
- •28. Схема сравнения на больше
- •29. Контроль по чётности
- •30. Классификация полупроводниковых бис зу
- •Основные параметры зу
- •31. Структурные схемы статических озу с произвольной выборкой
- •32. Элементы памяти статических озу на биполярн транз
- •33. Элементы памяти статических озу на мдп транзисторах
- •Элементы памяти статических озу на кмдп транзисторах
- •34. Элементы памяти и бис озу динамического типа
- •35. Общие сведения, основные параметры и классификация постоянных запоминающих устройств
- •Масочные пзу
- •36. Программируемые пзу
- •37. Репрограммируемые пзу
- •Рпзу с электрическим стиранием информации
- •38. Рпзу с ультрафиолетовым стиранием информации
- •51 Ацп параллельного типа
21. Сумматоры
Сумматором называют операционный узел ЭВМ, выполняющий операцию сложения двух чисел, представленных в двоичном коде. Известно, что все многообразие математических операций (сложение, вычитание, деление, возведение в степень, вычисление тригонометрических функций и т.п.) можно получить с помощью операций сложения прямых и обратных кодов чисел, сдвинутых влево или вправо на то или иное число разрядов. Поэтому скорость выполнения вычислительных процессов в ЭВМ существенно зависит от быстродействия сумматоров.
По принятой в ЭВМ системе счисления и кодирования сумматоры подразделяются на двоичные, десятичные, двоично-десятичные и др.
По способу организации суммирования чисел сумматоры могут быть комбинационными и накапливающими. В комбинационных сумматорах результат суммирования не запоминается. В накапливающих сумматорах, имеющих память, после добавления к содержимому сумматора очередного слагаемого происходит запоминание полученного результата.
По способу организации межразрядных переносов сумматоры делятся на параллельные, последовательные и c групповой структурой. В параллельных сумматорах суммирование одноименных разрядов чисел осуществляется одновременно (параллельно), а в последовательных — последовательно от младших к старшим. В сумматорах с групповой структурой суммируемые числа разбиваются на группы, построенные как параллельные сумматоры, а полученные в группах переносы складываются затем последовательно (параллельно-последовательные сумматоры) или параллельно. В последнем случае сумматоры называют параллельными с параллельно-параллельным переносом.
По способу тактирования различают синхронные и асинхронные сумматоры. В синхронных сумматорах для выполнения процесса суммирования отводится постоянное время независимо от разрядности суммируемых чисел, а в асинхронных после завершения процесса суммирования вырабатывается специальный сигнал (признак). Поэтому у асинхронных сумматоров среднее время суммирования меньше, чем у синхронных.
Одноразрядные двоичные сумматоры
В ЦВМ применяются одноразрядные двоичные сумматоры на два и три входа. Первые называются полусумматорами, вторые — полными одноразрядными сумматорами (ПОС).
Работа полусумматора определяется табл. 15.1, из которой видно, что полусумматор должен иметь два выхода: s0 — выход частичной суммы и c1 —выход сигнала переноса. Логические функции по выходам s0 и c1 , полученные на основании этой таблицы, имеют вид:
![]()
![]() (15.1)
(15.1)
Реализованная
по этим выражениям схема и ее УГО показаны
на рис. 15.1а, б.
![]()
![]()


|
a0 |
b0 |
s0 |
c1 |
|
0 0 1 1 |
0 1 0 1 |
0 1 1 0 |
0 0 0 1 |
Рис. 15.1
Входящий в нее элемент “ИСКЛЮЧАЮЩЕЕ ИЛИ” называют “сумматором по модулю 2” по той причине, что его выходная функция соответствует значению младшего разряда при суммировании двух одноразрядных двоичных чисел. На рис. 15.2 показаны варианты реализации сумматора по модулю 2 в различных базисах: И, ИЛИ, НЕ (рис.15.2, а), И-НЕ (рис. 15.2, б) и ИЛИ-НЕ (рис.15.2, в).
Из рисунка видно, что минимальная задержка формирования выходов функции s0 составит 3tзд.р.ср, где tзд.р.ср — среднее время задержки распространения сигнала в одном ЛЭ. Из рис. 15.2, а, б, в также следует, что для реализации сумматора по модулю 2 в том или ином базисе потребуется не менее 5 ЛЭ, а полусумматора (с учетом формирования переноса с1) — не менее 7 ЛЭ. Из этого следует, что синтез полусумматора на основании соотношений (15.1) и (15.2) оказывается нерациональным.
И
(15.3, а)
п![]() рямые
переменныеa0
и
b0
:
рямые
переменныеa0
и
b0
:
Д
(15.3, б)![]()
а)
б)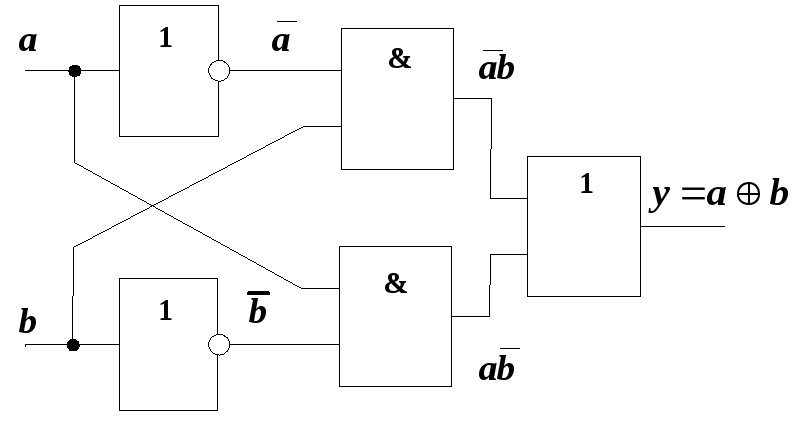

в)


