158_Tv / ТВ11

ЧАСТЬ 6

ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН

Лекция 11

1. ЗАКОН РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН

ЦЕЛЬ ЛЕКЦИИ: ввести понятие функции случайной величины и провести классификацию возникающих при этом задач; вывести закон распределения функции одного случайного аргумента и закон распределения суммы двух случайных величин; пояснить понятие композиции законов распределения.

Понятие о функции случайной величины

Среди практических приложений теории вероятностей особое место занимают задачи, требующие нахождения законов распределения и/или числовых характеристик функций случайных величин. В простейшем случае задача ставится следующим образом: на вход технического устройства поступает случайное воздействие ; устройство подвергает воздействие некоторому функциональному преобразованию и на выходе дает случайную величину (см. рис. 6.1). Нам известен закон распределения случайной величины , и требуется найти закон распределения и/или числовые характеристики случайной величины .

Можно выделить три основные возникающие задачи:

1. Зная закон распределения случайной величины (или случайного вектора ), найти закон распределения выходной случайной величины (или ).

2. Зная закон распределения случайной величины , найти только числовые характеристики выходной случайной величины.

3. В некоторых случаях (при особых видах преобразования ) для нахождения числовых характеристик выхода не требуется знать закон распределения входной случайной величины , а достаточно знать только его числовые характеристики.

Рассматриваем случайную величину , зависящую функционально от случайной величины , т. е. . Пусть случайная величина дискретна и известен ее ряд распределения:

Х:			…		…
			…		…		,

,

где .

При подаче на вход значения случайной величины на выходе получим с вероятностью . И так для всех возможных значений случайной величины . Таким образом, получаем табл. 6.1.

Таблица 6.1

		…		…
		…		…

Полученная табл. 6.1 в общем случае может не быть рядом распределения случайной величины , так как значения в верхней строке таблицы могут быть расположены в невозрастающем порядке, а некоторые могут даже совпадать.

Для преобразования табл. 6.1 в ряд распределения случайной величины необходимо упорядочить возможные значения по возрастанию, а вероятности совпадающих значений нужно сложить.

Для нахождения числовых характеристик случайной величины преобразовывать (6.1) в ряд распределения нет необходимости, так как их можно вычислить по таблице (6.1). Действительно, находя сумму произведений возможных значений случайной величины на их вероятности, получаем

. (6.1)

Таким образом, зная только закон распределения аргумента , можно найти математическое ожидание функции случайной величины.

Аналогично находим дисперсию случайной величины :

.

Аналогично определяем начальные и центральные моменты любых порядков случайной величины :

.

Для непрерывной случайной величины , имеющей плотность распределения , получаем

;

;

.

Видим, что для нахождения числовых характеристик функции вовсе не нужно знать ее закон распределения – достаточно знания закона распределения аргумента .

Теоремы о числовых характеристиках функций случайных величин

В некоторых задачах числовые характеристики системы случайных величин можно определить как функции числовых характеристик системы случайных величин . В этом случае не требуется даже знание закона распределения аргумента, например совместную плотность распределения , а достаточно иметь только числовые характеристики этой системы случайных величин. Для решения таких задач сформулированы следующие теоремы о числовых характеристиках функций случайных величин:

1. , 3. ,

2. , 4. ,

где – неслучайная величина.

5. для любого числа слагаемых, как независимых, так и зависимых, коррелированных и некоррелированных.

6. Математическое ожидание от линейной комбинации случайных величин равно той же линейной функции от математических ожиданий рассматриваемых случайных величин:

.

7. Дисперсия суммы случайных величин равна сумме всех элементов корреляционной матрицы этих случайных величин

.

Так как корреляционная матрица симметрична относительно главной диагонали, на которой находятся дисперсии, то последнюю формулу перепишем в виде

.

Если случайные величины не коррелированы, то справедлива теорема о сложении дисперсий:

.

8. Дисперсия линейной функции случайных величин определяется по формуле

.

9. Математическое ожидание произведения двух случайных величин равно произведению математических ожиданий плюс ковариация

.

Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий

.

10. Дисперсия произведения независимых случайных величин выражается формулой

Если случайные величины независимые и центрированные, получаем

.

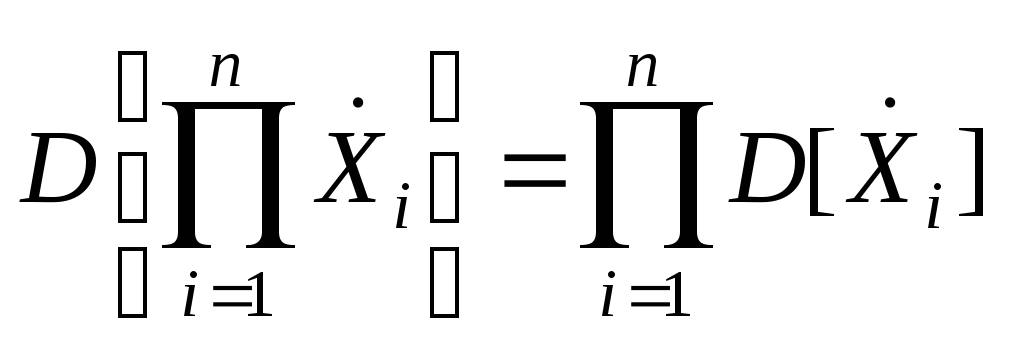Закон распределения функции случайного аргумента

Есть непрерывная случайная величина с плотностью распределения , связанная со случайной величиной функциональной зависимостью . Требуется найти закон распределения случайной величиной .

Рассмотрим случай, когда строго монотонна, непрерывна и дифференцируема на интервале всех возможных значений случайной величиной .

Функция распределения случайной величиной по определению есть . Если функция монотонно возрастает на участке всех возможных значений случайной величиной , то событие эквивалентно событию , где есть функция, обратная функции . Когда случайная величина принимает значения на участке , то случайная точка перемещается по кривой (ордината полностью определяется абсциссой) (см. рис. 6.2). Из строгой монотонности следует монотонность , и поэтому функцию распределения случайной величиной можно записать следующим образом:

.

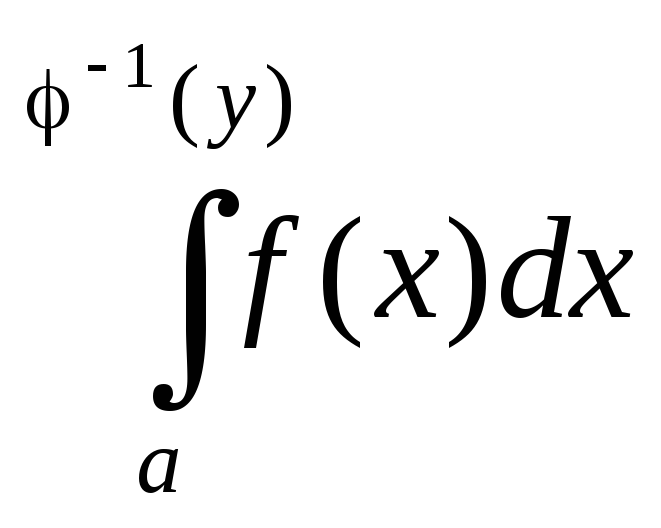Дифференцируя это выражение по , входящему в верхний предел интеграла, получаем плотность распределения случайной величиной в виде

. (6.2)

Если функция на участке возможных значений случайной величиной монотонно убывает, то, проведя аналогичные выкладки, получаем

. (6.3)

Диапазон возможных значений случайной величиной может быть в выражениях (6.2) и (6.3) от до .

Так как плотность распределения не может быть отрицательной, то формулы (6.2) и (6.3)можно объединить в одну

. (6.4)

Пример. Пусть функция случайной величины является линейной, т. е. , где . Непрерывная случайная величина имеет плотность распределения , и тогда, используя выражение (6.4), найдем закон распределения , учитывая, что обратная функция есть , а модуль ее производной равен ,

. (6.5)

Если случайная величина имеет нормальное распределение

,

то согласно (6.5) получаем

.

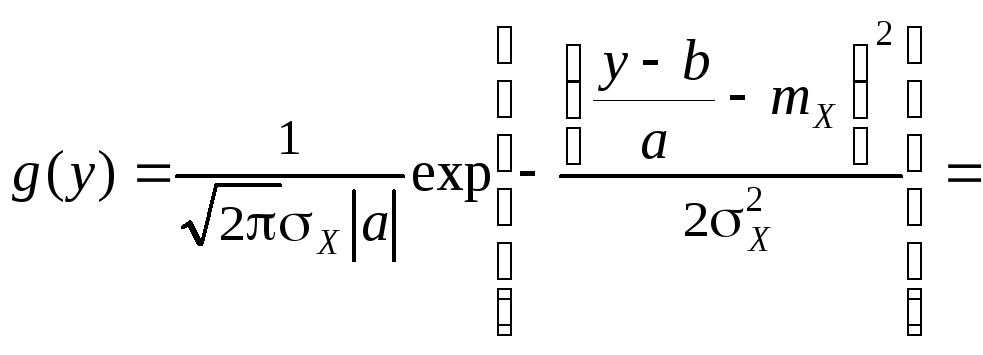
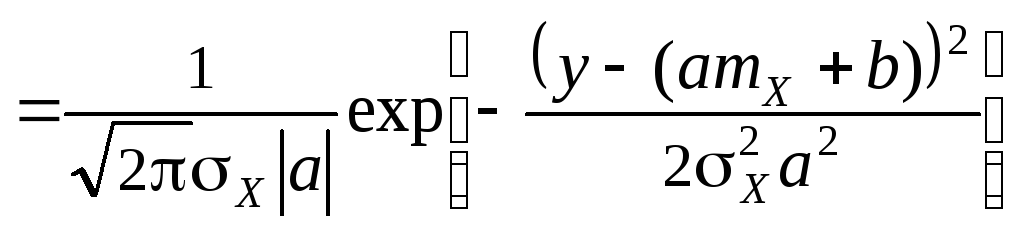Это по-прежнему нормальный закон распределения с математическим ожиданием , дисперсией и средним квадратичным отклонением .

В результате линейного преобразования нормально распределенной случайной величины получаем случайную величину , также распределенную по нормальному закону.

Закон распределения суммы двух случайных величин. Композиция законов распределения

Имеем систему двух непрерывных случайных величин и их сумму – случайную величину . Необходимо найти закон распределения случайной величины , если известна совместная плотность распределения системы .

Функция распределения – это площадь области на плоскости , где выполняется неравенство (см. рис. 6.3), т. е.

.

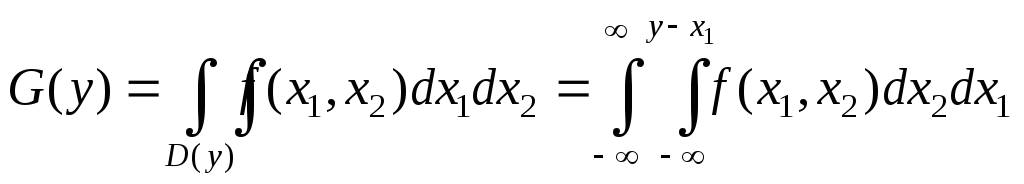Продифференцировав это выражение по , получаем плотность распределения вероятности случайной величины

.

Учитывая симметрию слагаемых, можно записать аналогичное соотношение

.

Если случайные величины и независимы, т. е. выполняется равенство , то две последние формулы примут вид:

; (6.6)

. (6.7)

В том случае, когда складываются независимые случайные величины и , то говорят о композиции законов распределения. Для обозначения композиции законов распределения иногда применяется символьная запись: .

Закон распределения называется устойчивым к композиции, если при композиции законов распределения этого типа получается снова тот же закон, но с другими значениями параметров. Например, если сложить две независимые нормальные случайные величины, то результирующая случайная величина будет иметь нормальный закон распределения, т. е. нормальный закон устойчив к композиции. Кроме нормального закона, устойчивыми к композиции являются законы распределения Эрланга, биноминальный, Пуассона.

105