5. Оптимизация Теоретические вопросы.

Общий подход к задачам: формализация (приоритет общего по отношению к частному), алгоритм (стандартность), реализация алгоритма. Вариантность.

Первый этап – решающий.

Для современного подхода к оптимизации характерна формализация задачи. Задача формулируется стандартным образом, после чего дальнейшее ее решение проводится на основе четкого однозначного рецепта – алгоритма. Однозначность в данном случае не означает, что отсутствуют варианты решений. Наоборот, проводится сравнение многих различных вариантов. Но алгоритм точно определяет, на каком этапе и как производится такое сравнение.

Формализация, во-первых, позволяет единообразно решать задачи из самых различных областей. Во-вторых, формализованные задачи приспособлены для решения на компьютерах. Применение вычислительной техники обеспечивает возможность перебора очень большого числа вариантов и выбора из них наилучшего. Поэтому формализация резко повышает эффективность процедуры решения задачи.

При формализации задачи оптимизации возникает важное противоречие. Задача распадается на три основных этапа:

1) формулирование задачи, приведение ее к одной из стандартных форм;

2) нахождение оптимальных условий на основе алгоритма оптимизации;

3) реализация оптимальных условий на практике. Методы решения на первом и втором этапах взаимно противоположны: второй этап, как правило, целиком формализован на основе алгоритма решения, а первый этап – неформален. Здесь не поможет никакая математика. Первый этап решения задачи связывает конкретные особенности объекта с общим методом решения. Если задача оптимизации плохо сформулирована, то совершенно правильное ее решение даст результат, абсурдный для практики. Иногда именно хорошая формулировка задачи определяет успех оптимизации в целом. Некоторые проблемы, возникающие при формулировании задач оптимизации, проиллюстрируем на примерах.

Таким образом, на этапе формулирования задачи приходится учитывать физико-химические особенности процесса, его экономичность, общее развитие промышленности, рыночную конъюнктуру и множество других обстоятельств.

Как правило, формулировка задачи оптимизации включает выбор критерия оптимальности, установление ограничений, выбор оптимизирующих факторов и запись целевой функции.

Критерий, множество критериев, выбор главного, корректность выбора.

Универсальный подход ко многим задачам, которые можно решать иначе. Родство к подбору критерия. Формулировка задачи. Выбор критерия оптимальности.

Требования:

единственность (экономика, технология, экология…);

численность (баллы для качественных задач);

монотонная зависимость от факторов как основное средство против множественности решений.

Критерий оптимальности – это главный признак, по которому судят о том, насколько хорошо функционирует система, работает данный процесс, насколько хорошо решена задача оптимизации. О работе судят по ее результатам.

Поэтому критерий оптимальности является одним из результатов работы, одним из выходов системы. Чтобы выбранный критерий оптимальности можно было эффективно использовать на следующем этапе, он должен удовлетворять трем основным требованиям.

1. Критерий оптимальности должен быть единственным. Это самое тяжелое требование. Дело в том, что, как правило, нас интересует ряд выходов системы и мы хотим, чтобы по всем им система была наилучшей. Иногда говорят так: оптимальным является такое ведение технологического процесса, при котором производительность установки и качество продукта максимальны, а затраты и потери минимальны. При внешней привлекательности такая постановка задачи утопична и потому объективно вредна. Так вести процесс невозможно.

Обычно наиболее обоснованы такие экономические критерии, как прибыль, норма прибыли, рентабельность, приведённый доход, себестоимость. Однако чаще всего характер зависимости этих критериев от входных параметров системы сложен. Для упрощения задачи зачастую пользуются технологическими критериями, например производительностью, чистотой продукта, выходом продукта, селективностью. Каждый технологический критерий в конечном счете связан с экономикой: чем больше производительность, тем выше будет прибыль; чем выше чистота, тем меньше будут затраты на следующих стадиях, и т. д. При оптимизации производства в целом или его крупных подразделений естественно использовать экономические критерии. Технологические критерии удобны при оптимизации более мелких объектов: отдельного узла, аппарата, небольшой цепочки аппаратов, т. е. при локальной оптимизации. При их применении следует особенно тщательно учитывать особенности процесса: критерий, пригодный в одних условиях, может быть совершенно не применим в других условиях.

2. Критерий оптимальности должен выражаться числом. В противном случае сопоставление разных вариантов становится крайне затруднительным.

3. Обязательное и крайне важное свойство критерия оптимальности: его величина должна изменяться монотонно при улучшении качества функционирования системы. Это значит, что оценивать объект можно по принципу: «чем больше критерий, тем лучше», либо «чем меньше критерий, тем лучше», но ни в коем случае не по принципу: «вот это значение критерия оптимально и отклоняться от него не следует». Что требуется, «больше» или «меньше», определяется физическим или экономическим смыслом критерия. Хорошо, когда прибыль велика, но когда себестоимость мала; когда велика производительность, но малы потери. Умножив любой критерий на –1, мы превратим «больше» в «меньше» и наоборот. Но вот критерий, обладающий некоторым оптимальным значением, от которого нежелательно отклоняться, не годится. Например, в лекарственной смеси содержание того или иного ингредиента не может являться критерием оптимальности: иначе мы бы получили не смесь заданного состава, а максимальную концентрацию одного вещества.

Если для какого-то параметра, характеризующего систему, существует оптимальное значение, то либо этот параметр – не критерий оптимальности, а оптимизирующий фактор (см. ниже), либо критерием является не величина параметра, а отклонение этой величины от заданного значения.

Ограничения – категорические условия (дополнительные критерии, предельные возможности по количеству, качеству, технологии, экономике, конъюнктуре, охране труда и среды обитания…). По форме это равенства и неравенства.

Ограничения - Условия, которые необходимо соблюдать независимо от того, как их соблюдение повлияет на величину критерия оптимальности.

Следующие группы ограничений:

• по количеству и качеству сырья и продукции – состав сырья, как правило, задается не нами и менять его нельзя; количество сырья также может быть ограничено; выпуск продукции не должен быть больше того, что можно реализовать; качество продукта не должно быть ниже стандарта или требований заказчика;

• по условиям технологии – расход воздуха не может превышать производительность вентилятора; температура не может быть выше предела, при котором портится материал аппарата или катализатор; размеры аппаратов изменять мы не можем и т. д.;

• по экономическим и конъюнктурным соображениям – капитальные затраты не должны превышать выделенной суммы; срок ввода нового производства не должен быть позже запланированного; нельзя применять методы и устройства, защищенные чужими

патентами;

• по соображениям охраны труда и окружающей среды – это чрезвычайно важная группа ограничений, жесткость которых все возрастает.

Кроме классификации по смыслу ограничения можно различать по формально-математическим признакам. Так, выделяют ограничения типа равенств и типа неравенств.

Ограничения типа равенств устанавливают определенное значение того или иного параметра:

Здесь fi – один из параметров, аi – задаваемое для него значение. Например, в конкретных условиях работы задаются численные значения, характеризующие состав сырья, размеры аппаратов, нагрузку на аппарат и т. д.

Ограничения типа неравенств определяют пределы, в которых допустимо изменение параметров процесса:

Два первых ограничения (7.3) задают односторонние пределы (например, производительность не ниже заданной; температура не выше той, на которую рассчитан материал). Третье ограничение – двустороннее (например, температура жидкости в пределах от температуры замерзания до температуры кипения).

Ограничения

1-го рода: на входные факторы;

2-го рода: на промежуточные и выходные величины, что сложнее.

Наконец, в расчетных процедурах нахождения оптимума большую роль играет деление ограничений по следующему признаку: ограничения 1-го рода – условия (7.2) или (7.3), где в качестве параметров f фигурируют входные факторы; ограничения 2-го рода, где параметрами служат различные функции входов, например результаты процесса или, скажем, температуры в каких-то точках внутри аппарата.

Оптимизирующие факторы – управляемые входы (температура…).

Оптимизирующие факторы – те из входов системы, которые в процессе оптимизации относят к управляющим. Это те воздействия, которые мы применяем для оптимизации процесса. Остальные факторы при этом не регулируются, хотя их значения, разумеется, учитывают при определении оптимальных условий: эти факторы фигурируют в задаче в качестве ограничений типа равенств.

Оптимальное проектирование – много факторов (недорого на модели). Оптимальное управление (динамическое программирование) – факторов поменьше.

Число оптимизирующих факторов зависит от того, на какой стадии разработки производства осуществляется оптимизация. Если производство еще проектируется (оптимальное проектирование), то к оптимизирующим целесообразно отнести как можно большее число факторов. Действительно, на этой стадии варьировать факторы проще всего: изменение значений осуществляется не в действительности, а на математической модели. Поэтому здесь желательно найти оптимальные значения максимального числа факторов.

Но задача оптимизации возникает и после пуска производства (оптимальное управление). При этом число оптимизирующих воздействий становится существенно меньшим. Часть факторов мы уже не можем менять, например размеры аппаратов. Но и не все остальные факторы целесообразно теперь регулировать. Дело в том, что чем больше управляющих факторов, тем сложнее система управления, сложнее ее математическая модель. При очень большом числе факторов она может стать столь сложной, что компьютер, рассчитывающий оптимальные режимы, перестанет поспевать за изменением условий протекания процесса: рекомендации по оптимизации придут, когда реализовать их уже поздно. Все это заставляет использовать для оптимального управления сравнительно небольшое число факторов.

Целевая функция – критерий оптимальности, его экстремум, оптимальные значения факторов при нем. Функционал, распределенные факторы, характер распределения. Условный экстремум (на границе, при ограничениях и т.п.).

Целевая функция – это синоним критерия оптимальности, но это критерий, рассматриваемый как функция входных факторов:

Чем больше (или чем меньше) значение F, тем лучше. Поэтому можно дать такое определение оптимума: оптимум – это экстремум (либо максимум, либо минимум) целевой функции. Те значения факторов хj, при которых достигается оптимум, называют оптимальными.

Таким образом, математически задача оптимизации формулируется как задача отыскания экстремума. При этом в точке экстремума должны соблюдаться все ограничения. Поэтому во многих случаях оптимум приходится искать на краю области допустимых значений,

за пределы которой нельзя выйти из-за ограничений (рис. 7.1). На рисунке отрезок аb есть область допустимых значений, определяемая ограничением a ≤ x ≤ b. Максимум функции F расположен правее точки b, но оптимальным будет значение x = b, поскольку большие значения х запрещены ограничением.

Рис. 7.1. Целевая функция с оптимумом на краю допустимой области

Методы отыскания оптимума:

- аналитические (на основе вариационного исчисления), они играют роль теоретической основы

- численные (поисковые, при вычислимой функции, в т.ч. при неявной форме уравнений относительно выходных величин)

- экспериментальные (при невычислимой, но воспроизводимой функции).

Методы отыскания оптимума можно разделить на три основные группы.

1. Аналитические методы. Их применяют, например, когда мы можем продифференцировать целевую функцию и искать экстремум исходя из условия равенства нулю производных. Условие отыскания экстремума при аналитической оптимизации - нулевое значение 1-х производных по факторам одинаковом знаке 2-х.

2. Численные, или поисковые методы. Для их применения нужно, чтобы целевая функция была вычислимой : должен быть известен алгоритм, по которому можно рассчитать значение критерия оптимальности при заданных значениях факторов.

3. Методы, применяемые, если целевая функция невычислима. Практически это значит, что вид функции неизвестен. Тогда остается одно: планировать и реализовывать эксперимент так, чтобы в результате достигнуть района оптимума. Это – экспериментальная оптимизация, составляющая важный раздел планирования эксперимента.

Максимум и минимум. Седла и перегибы, локальность, ограничения, нормальные уравнения. Множественность решения: глобальность и локальность. Поверхность отклика, ее симметрия как источник глобальной и локальной неоднозначности.

Пусть целевая функция задана формулой (7.4). Классический метод отыскания экстремума заключается в решении системы

Левые части уравнений (7.5) – функции от факторов х1, х2, ..., хn. Поэтому решение системы может дать значения x1опт , x2опт , ..., xn_опт , являющиеся оптимальными значениями факторов; их совокупность определяет наилучшее решение задачи. Если оптимизируется технологический процесс, то этому решению соответствует оптимальный

режим. Однако следует убедиться, что полученные значения действительно оптимальны. Для этого необходимо выяснить:

1) действительно ли решение системы (7.5) определяет экстремум, поскольку известно, что условию (7.5) может удовлетворять и седловая точка, или точка перегиба;

2) получен ли экстремум нужного знака (максимум, если нас интересует максимум, или минимум в обратном случае);

3) если система имеет несколько решений, то какое из них отвечает глобальному оптимуму, а какие – локальным. Так, если зависимость имеет несколько максимумов, то глобальным будет тот из них, который выше всех остальных; остальные будут локальными;

4) все ли ограничения соблюдаются в точке экстремума. Рассмотрим некоторые важные задачи оптимизации. Одна из разобранных выше задач, а именно расчет коэффициентов методом наименьших квадратов (см. разд. 2.3) – типичная задача такого рода. В ней критерий оптимальности – сумма квадратов S; оптимизирующие факторы – значения рассчитываемых параметров. Ограничения в изложенном варианте отсутствуют. Система (7.5) – это система нормальных уравнений (2.42).

Примеры решаемых небольших задач. Сложные или объемистые задачи – для численных методов. Обратимая экзотермическая реакция первого порядка, оптимальная температура: Т_опт=(Е₂-Е₁)/(Rln(A₂/A₁E₂/E₁C_B/C_A)).

Если химическая реакция проходит без побочных стадий, то удается принять очень простой критерий оптимальности – скорость реакции (см. пример 7.2). Согласно схеме, данной в предыдущем разделе, теперь нужно установить ограничения и выбрать оптимизирующие факторы. Но часто бывает удобно сначала записать целевую функцию, а уже потом перейти к ограничениям и оптимизирующим факторам. Так поступим и мы. Для определенности рассмотрим реакцию

Таким образом, наш критерий зависит от трех параметров: температуры и концентраций сА и сВ. По-видимому, эти три величины можно было бы избрать в качестве оптимизирующих факторов. Но необходимо учесть, что концентрации сА и сВ не относятся ко входам рассматриваемой системы. Они сами получаются как результат реакции. Ясно, что для увеличения скорости следовало бы иметь как можно большее значение сА и как можно меньшее значение сВ. Цель же процесса – противоположная: увеличить сВ и уменьшить сА. Поэтому концентрации нельзя рассматривать как независимые факторы.

Итак, есть лишь один независимый фактор, которым можно влиять на F – температура. Рассматриваемая задача обычно называется задачей об оптимальной температуре химической реакции. Но при разных концентрациях влияние температуры может быть

различным. Поэтому будем решать задачу в такой постановке: зафиксируем некоторые значения сА и сВ и при этих значениях найдем оптимальную температуру. Таким образом, в данном решении концентрации веществ А и В выступают в роли ограничений типа равенства.

Кроме того, учтем одно ограничение типа неравенства, которое существует в любой практической задаче: температура не может превысить некоторого максимального значения Тмакс :

Прежде чем обращаться к формуле (7.5), рассмотрим два случая, когда оптимум можно найти из физических соображений, без расчета. Если реакция необратима, т. е. А2 = 0, то в правой части формулы (7.6) остается только первый член, который с повышением температуры все время растет. Максимум в смысле условия (7.5) отсутствует.

Тогда оптимум определяется ограничением: следует поддерживать максимально допустимую температуру

Если реакция обратима, но эндотермична, т. е. E1 > E2, то результат рассуждений тот же, что и в предыдущем случае. Действительно, с повышением температуры равновесие сдвигается вправо и скорость прямой реакции возрастает. Поэтому оптимум определяется формулой (7.6).

Если реакция – обратимая экзотермическая, то к решению потребуется применить иной подход. В этом случае с повышением температуры вначале более существенным будет возрастание скорости

прямой реакции; обратная еще слишком медленна. При дальнейшем увеличении температуры обратная реакция, имеющая большую энергию активации, начинает «нагонять» прямую. При данном составе смеси существует температура Tравн, при которой смесь находится в равновесии: r = 0; затем ход реакции смещается влево.

Где-то посередине имеется температура, при которой суммарная скорость реакции максимальна. Это и есть оптимальная температура Топт . Для ее расчета запишем условие (7.5) для формулы (7.6):

Здесь записана частная производная по T, поскольку она берется при фиксированных значениях cA и cB.

Из уравнения (7.9) несложными преобразованиями можно получить формулу для оптимальной температуры:

Ступенчатое охлаждение. Из соотношения (7.10) следует, что чем выше cA и чем меньше cB, тем выше Топт; по мере роста степени превращения величина Топт уменьшается. При cB→0, согласно формуле, Топт →∞. Поэтому на начальном участке реактора следует устанавливать максимально допустимую температуру Tмакс, а с момента, когда рассчитанная по этому уравнению Топт сравнивается с Tмакс, дальнейшее изменение температуры должно определяться уравнением (7.10). Такую зависимость иллюстрирует кривая 1 на рис. 7.2, изображающая оптимальный ход температуры в зависимости от степени превращения.

Рис. 7.2. Изменение оптимальной температуры в зависимости от степени превращения для обратимой экзотермической реакции

Реально осуществить такое распределение температуры чрезвычайно трудно. Действительно, на начальном участке следовало бы поддерживать постоянную максимальную температуру, что крайне сложно: здесь скорость реакции очень велика, выделение тепла максимально и полностью отвести его вряд ли удастся. Поэтому применяют другие распределения, более или менее приближающиеся к оптимальному. Так, ломаная 2 на рис. 7.2 показывает ход температуры в пятислойном каталитическом реакторе, в каждом слое которого реагирующая смесь адиабатически разогревается за счет тепла реакции, а между слоями охлаждается в теплообменнике. Такое распределение температур приведет к несколько худшим результатам (большему потребному объему катализатора), чем задаваемое кривой 1, но его сравнительно легко осуществить. Чем больше ступеней катализа, тем ближе ломаная к оптимальной кривой.

Если реакцию проводят в аппарате смешения, то во всем его объеме имеем одну и ту же степень превращения. Ей соответствует одна точка на кривой 1 (см. рис. 7.2), соответствующая оптимальной температуре для данного аппарата.

Параллельно работающие аппараты ИС. Первый порядок, необратимо, проскок – это потеря.

Оптимальное распределение потока по параллельно работающим аппаратам. Это одна из задач, возникающих при оптимальном управлении.

Рис. 7.3. Схема распределения потока по аппаратам

Реакция 1-го порядка А → В проводится в n параллельно соединенных реакторах идеального смешения (рис. 7.3). Как оптимально распределить поток между аппаратами? Будем считать, что в общем случае объемы аппаратов V1, V2, …, Vn разные и что константы скорости реакции в различных аппаратах k1, k2, …, kn тоже разные (например, вследствие неодинаковой активности катализатора).

Естественно принять за критерий оптимальности сумму потерь вещества А, т. е. считать наилучшим такое распределение, при котором потери вещества А вследствие неполноты реакции минимальны.

В каждом i-м аппарате при расходе vi эти потери в единицу времени составляют vi*c_Ai; тогда для всех аппаратов можно записать:

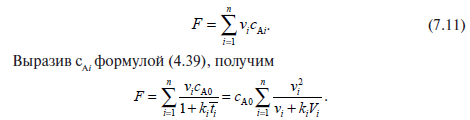
Обозначим kiVi = ai. Величина ai характеризует относительную производительность i-го аппарата: чем больше эта величина, тем больше продукта может получиться в нем в единицу времени. Теперь можно записать:

Прежде чем применить к целевой функции (7.12) условие (7.5), обратим внимание на существующее в этой задаче ограничение типа равенства: сумма расходов через все аппараты равна общему расходу через систему:

Учтем, что частная производная от этого выражения по любому vi равна –1, поскольку v – постоянная, а под знаком суммы от vi зависит только один член, а именно vi , и частные производные от всех остальных членов равны 0. Тогда по теореме о производной функции от функции для производной по любому vi любой функции f от vn будем иметь:

При оптимальном распределении расход через каждый аппарат пропорционален относительной производительности этого аппарата. Чем больше аi , тем больше vi . Простое преобразование формулы (7.18) дает

При оптимальном распределении потока концентрации вещества на выходе из всех аппаратов одинаковы. Условие (7.19) позволяет просто осуществлять оптимальное регулирование распределения потока: концентрация вещества А на выходе из всех аппаратов должны быть одинаковой; если в каком-то аппарате она больше, чем

в остальных, расход из этого аппарата следует уменьшить, и наоборот, если сА меньше средней, расход надо увеличить.

Оптимальный режим достигается при равных выходных концентрациях: простое управление при разных константах скорости (катализ, температура, объем).

Численные методы. Аналитическую производную трудно, а чаще невозможно вывести: дискретность, край области, алгоритмическое задание критерия, громоздкость. Поэтому превалируют численные методы.

Простой перебор (варианты, включая Монте-Карло).

Сканирование (непрерывные функции, но не только).

Узлы. Одномерное сканирование. Управление шагом. Выбор интервала неопределенности. Правило останова

Поиск оптимума численными методами

Численные методы поиска применяют, во-первых, когда в точке экстремума отсутствуют производные. Так, изменение целевой функции может носить дискретный характер, например при сравнении разных вариантов оформления процесса, когда F меняется не непрерывно, а скачком от одного варианта к другому. Но производные в точке экстремума могут отсутствовать и у непрерывной функции. Как правило, это происходит, если экстремум расположен на краю области допустимых значений. На рис. 7.1 максимум лежит на краю области, в этой точке производная отсутствует. Имеется «производная слева», но она не равна нулю. В задачах оптимизации такую точку рассматривают как «законный» экстремум (в данном случае – максимум). Часто бывает и так, что целевая функция в точке экстремума дифференцируема, но она задана таким образом, что продифференцировать ее в общем виде не удается, вследствие чего приходится

обращаться к численным методам. Это обычно связано с тем, что функция задана не формулой, а алгоритмом вычисления при заданных значениях аргументов (факторов). Если бы не было и алгоритма, функция была бы невычислимой и следовало бы применить экспериментальную оптимизацию (см. разд. 7.4).

Наконец, иногда имеется принципиальная возможность записать и решить систему (7.5), но соответствующие вычисления столь громоздки, что численный метод оказывается проще.

В наиболее общем виде численные методы сводятся к тому, что вычисляется ряд значений F при различных значениях аргументов; сопоставление этих значений показывает, в каком направлении нужно двигаться в пространстве факторов, чтобы приблизиться к оптимуму.

Оптимизация перебором применяется, если число возможных вариантов конечно. Тогда достаточно рассчитать целевую функцию для всех этих вариантов и выбрать наибольшее (или наименьшее) значение. Например, мы можем рассчитать F для случаев протекания

процесса в аппаратах всех стандартизованных размеров и выбрать лучший вариант. Перебор легко осуществляется на компьютере, причем все варианты (например, нормали) могут быть заранее записаны в памяти машины.

Несмотря на крайнюю простоту метода, он часто оказывается чрезвычайно эффективным, поскольку возможности перебора для машины неизмеримо выше, чем для человека. Применение перебора позволяет найти такие варианты, до которых без компьютера дойти

практические невозможно.

Суть метода Монте-Карло заключается в следующем: процесс описывается математической моделью с использованием генератора случайных величин, модель многократно обсчитывается, на основе полученных данных вычисляются вероятностные характеристики рассматриваемого процесса. Например, чтобы узнать методом Монте-Карло, какое в среднем будет расстояние между двумя случайными точками в круге, нужно взять координаты большого числа случайных пар точек в границах заданной окружности, для каждой пары вычислить расстояние, а потом для них посчитать среднее арифметическое.

Сканирование – метод, близкий к перебору, но применяемый к непрерывным функциям. Рассмотрим для примера одномерное сканирование – случай, когда ищется максимум функции от одного фактора (как я уже говорил, поиск минимума осуществляется точно

так же). Будем считать, что мы задались пределами изменения фактора х от а до b. Здесь а и b – ограничения, которые можно установить в любой реальной задаче: никогда не бывает так, что мы может задать любые, ничем не ограниченные значения х.

Таким образом имеется интервал [а, b], на котором мы хотим отыскать экстремум целевой функции; его называют интервалом неопределенности. При этом практически нам не нужно определять точку экстремума абсолютно точно. Достаточно сильно сузить интервал неопределенности. Например, если мы узнаем, что оптимальная температура, соответствующая максимуму целевой функции, заключена в пределах от 380 до 381 К, то большая точность не нужна. В промышленных условиях вряд ли удастся регулировать температуру с точностью выше 1 К.

Итак, в одномерном случае задача поиска экстремума сводится к сужению интервала неопределенности. Методом сканирования эта задача решается следующим образом. Выбираем целое число q - число значений целевой функции, которое придется рассчитывать.

Находим интервал Δx :

Откладываем от точки а до точки b интервалы Δх (рис. 7.4). Концы каждого интервала назовем узлами; на рис. 7.4 каждый узел обозначен крестиком.

Рис. 7.4. Поиск экстремума сканированием: a, b – границы интервала неопределенности

В каждом узле рассчитываем F(х) (см. точки на рис. 7.4). Теперь мы можем принять за максимум наибольшее из полученных значений – на рисунке это 4-я точка слева. К концу расчета интервал неопределенности δ составит 2Δх: истинный максимум может лежать

либо справа, либо слева от полученной наилучшей точки (штрихи на рис. 7.4). Таким образом,

Формула (7.21) определяет эффективность метода. При сканировании для достижения достаточно малого значения δ величина q должна быть велика. Метод малоэффективен, но удобен для первоначального исследования функции, поскольку дает возможность представить ее вид на всем отрезке, установить число экстремумов и их локализацию.

Переменный шаг. Унимодальность. Более эффективно сканирование с переменным шагом: сократив интервал неопределенности, мы продолжаем поиск внутри этого интервала, уменьшая в свою очередь Δх. Например, двигаясь на рис. 7.4 от а к b и дойдя до 5-й слева точки, можно двинуться в обратном направлении меньшими шагами; затем эту процедуру можно продолжить, снова двигаясь вправо и снова уменьшив шаги и т.д. Такой вариант часто называют методом тяжелого шарика (если ищется минимум, то движение точек по кривой функции похоже на скатывание шарика в ложбину, когда он раз за разом проскакивает нижнее положение, колеблясь около него и постепенно приближаясь к нему).

Многомерное сканирование. Метод неэффективен, но универсален. Направленный поиск. Обучение алгоритма. Сканированием можно исследовать функции более чем одного фактора. Так, участок на плоскости (факторное пространство для двух факторов) можно покрыть сетью узлов и таким образом исследовать поведение функции на этом участке. В принципе это возможно в любом n-мерном пространстве, но по мере увеличения n резко растет число необходимых расчетов и падает эффективность метода.

Другие методы поиска более эффективны, но не обладают той универсальностью, которой отличается сканирование. Их эффективность связана с тем, что это методы направленного поиска, в которых не просто исследуется область факторного пространства, а

происходит продвижение в этом пространстве в сторону искомого экстремума. Уже описанное выше сканирование с переменным шагом означает направленность поиска: вблизи экстремума прекращается дальнейшее движение вдоль оси х и начинается сгущение точек около экстремума.

Направленность поиска требует соблюдения некоторых условий, ограничивающих применимость методов. Прежде всего направленный поиск дает надежный результат, если функция унимодальна.

Наиболее просто (хотя и не вполне строго) унимодальную функцию можно определить так. В допустимой области она имеет только один экстремум нужного знака (один максимум, если ищем максимум, или один минимум в противном случае). Например, на рис. 7.5 функция 1 унимодальна. Функция 2 унимодальна, если ищем максимум, и неунимодальна при поиске минимума (два минимума: при х = а и при х = b). Функция 3 неунимодальна.

Рис. 7.5. Графики унимодальных и неунимодальных функций

Глобальность. Одномерная и многомерная оптимизация. Методы направленного поиска способны привести в точку одного из экстремумов, но не позволяют установить, единственный ли это экстремум, а если известно, что не единственный, то в какой экстремум мы попали: глобальный (экстремальный для всей области) или локальный (другие точки могут оказаться выше в случае максимума

или ниже для минимума). Если при решении задачи оптимизации появится подозрение, что мы встретились с неунимодальностью, можно грубо исследовать функцию сканированием и выделить область глобального экстремума.

Еще одно важное свойство функции F, учитываемое при выборе метода поиска, – это число факторов. Здесь различаются два основных случая. Первый, когда F зависит только от одного фактора, F = F(x): тогда говорят об одномерном поиске. Второй, когда факторов больше одного, – многомерный поиск. Причем почти все методы многомерного поиска принципиально применимы при любом числе факторов n > 1, тогда как при n = 1 используются иные, одномерные, методы. Лишь немногие методы, как, например, сканирование, применимы и для одномерного, и для многомерного поиска

Локальная минимизация. Обратная задача моделирования как частный случай оптимизации. Идентификация структурная и параметрическая. Модель состояния и модель наблюдения. (какая-то жесть, думаю, это не столь важная инфа:D)

Философия применения модели наблюдения как оболочки структурной модели состояния.

Интервал неопределённости. Шаг поиска. Точность. Правила останова.

Одномерная (однофакторная) оптимизация. Требования к критерию оптимизации: численная непрерывность и дифференцируемость, унимодальность.

Метод дихотомии. Ход процесса. Правило выбора направления и интервала неопределенности. Правило останова. Сходимость. Правило останова, связь с вариационным исчислением. Интервал неопределенности. Эффективность и число шагов. Ознакомление

Как и при описании сканирования, будем искать максимум на отрезке [а, b], показанном на рис. 7.6. Для этого разделим отрезок пополам – на рисунке точка л (левая). Рассчитаем значение F(л) в этой точке. Пока еще ничего нельзя сказать об экстремуме, кроме того, что он принадлежит нашему отрезку.

Рис. 7.6. График поиска максимума методом дихотомии

Выберем малое приращение фактора, равное ε, и поставим на отрезке правую точку п = л + ε. Рассчитаем F(п). Поскольку F(л) > F(п), как изображено на рис. 7.6, можно утверждать, что если F(x) унимодальна, то максимум находится в левой половине отрезка.

Теперь отбросим правую половину отрезка (на ней максимума нет). Для этого правый конец (точку b) перенесем в точку л и обозначим ее буквой b (такая операция переименования не вполне привычна для традиционной математики, но в алгоритмических языках она чрезвычайно распространена). На рис. 7.6 этот перенос показан стрелкой. Разумеется, при F(л) < F(п) в точку л мы перенесли бы точку а. Можно перенести конец отрезка и в точку п, но так как л и п близки, то это почти одно и то же.

После того как правый конец отрезка перенесен, задача вернулась к исходным условиям: задан отрезок от а до b, на котором нужно найти максимум. Поэтому проводится следующий цикл расчета, ничем не отличающийся от предыдущего, кроме значения b. Снова делим пополам отрезок, ставим вспомогательную точку на расстоянии ε, переносим в середину либо правый, либо левый конец. Такой алгоритм (расчет слагается из одинаковых циклов, различающихся лишь начальными условиями) называют итерационным.

В принципе итерации можно проводить до бесконечности: делить пополам все меньшие отрезки. Поэтому в любом итерационном алгоритме нужно задать правило останова, определяющее, когда можно прекращать расчет, считая, что полученная точность уже достаточна.

Например, можно остановить итерации, когда интервал неопределенности окажется не больше ε:

Метод золотого сечения (0.382, 0.618). Правило выбора направления и интервала неопределённости. Отбрасывание «лишней» из 4 точек. Правило останова.

Пропорция золотого сечения (деления отрезка в среднем и крайнем отношении) определяется так. Отрезок длины l делится на две части m и l – m так, чтобы меньшая часть относилась большей, как большая ко всему отрезку:

Рис. 7.7. График поиска максимума методом золотого сечения

Рассмотрим опять отрезок [а, b], на котором нужно найти максимум (рис. 7.7). Поиск максимума начинаем с того, что делим отрезок слева и справа в соответствии с пропорцией золотого сечения и получаем точки л и п. Расстояние от а до л составляет 0,382 (b – а), от а до п 0,618(b – а). В этих точках рассчитаем значения F. Как и в методе дихотомии, здесь имеем две точки л и п, но расстояние между ними не мало и вероятность того, что точка экстремума попадет между ними, достаточно велика. Поэтому, например, если F(п) > F(л) (см. рис. 7.7), то нельзя сказать, в какой из трех частей отрезка окажется

максимум – он может быть и в средней части отрезка (левая штриховая линия на рисунке), и в правой (правая штриховая линия). Но в левой части (мы приняли, что функция унимодальна) максимума быть не может. Поэтому можно ее отбросить – перенести левый конец отрезка в точку л, назвав ее а (левая стрелка). Теперь задача как будто вернулась к исходной формулировке: найти максимум на отрезке [а, b]. Но на этом отрезке уже есть точка (точка п, см. рис. 7.7), в которой рассчитано значение функции, причем благодаря свойству (7.24) эта точка, отсекавшая от предыдущего большего отрезка справа ~38,2%, отсекает от нового, уменьшенного отрезка справа ~61,8%, т. е. и на новом отрезке она является точкой золотого сечения. Теперь, на новом этапе расчета мы можем назвать ее л (см. правую стрелку на рис. 7.7) и поставить на уменьшенном отрезке не две точки для расчета F, а только одну – правую (на рис. 7.7 обозначена

треугольником). Таким образом, на каждом этапе расчета, кроме самого первого, мы должны рассчитывать F только в одной точке, что повышает эффективность метода. В качестве правила останова можно воспользоваться формулой (7.22).

Эффективность метода определяется следующим образом. После двух первых расчетов F и после каждого последующего остающийся интервал неопределенности составляет 0,618 предыдущего. Тогда при q расчетах целевой функции

При q > 4 эффективность метода золотого сечения выше, чем метода дихотомии; при небольших q, порядка 10 – 20, эффективность обоих методов близка, но при q > 20 метод золотого сечения становится заметно эффективнее.

Таким образом, если не нужно очень точно фиксировать абсциссу оптимума, то можно пользоваться любым из этих методов. Если нужна высокая точность (или если каждый расчет громоздок), то предпочтительнее метод золотого сечения. Впрочем, при малых q часто целесообразно ограничиться сканированием.

Многомерная (многофакторная) оптимизация.

Классификация методов включает следующие основные альтернативы: градиентные и прямого поиска, управление шагом и направлением регуляризированное или стохастическое, без моделирования поведения целевой функции и с применением такового, но встречаются и более детализированные варианты.

Метод покоординатного спуска (Гаусса-Зейделя). Ход процесса. Управление шагом поиска. Правило останова.

Правило останова – правило, применяемое для вынесения решения, нужны ли дальнейшие эксперименты. Оно определяет, когда можно прекращать расчет, считая, что полученная точность уже достаточна.

Метод покоординатного спуска. Выбираем координаты начальной точки поиска х1Н и x2Н, т. е. те значения х1 и х2, от которых мы начнем искать оптимум, единичные приращения обоих факторов (шаги) Н1 и Н2, а также малые приращения факторов ε1 и ε2. Выбор всех этих величин определяется физическим смыслом задачи и той информацией о ней, которой мы располагаем заранее.

Рис. 7.8. График движения в пространстве факторов при покоординатном спуске

Рассчитываем значение F(x1Н , x2Н) в точке 1 (рис. 7.8). Далее, не меняя величины х2, начинаем двигаться вдоль оси х1, давая на каждом шаге этому фактору приращение H1 (или –Н1, в зависимости от того, при движении в какую сторону будет наблюдаться рост F ). На каждом шаге – в точках 2, 3, 4 и т. д. – проводится расчет F. Шаги продолжаются до тех пор, пока продолжается рост F. Неудачными будем считать те шаги, на которых получено значение F меньшее, чем на предыдущих шагах (на рисунке они обозначены крестиками). После первого неудачного шага (точка 6) возвращаемся в предыдущую точку (в данном случае в точку 5), фиксируем величину х1 и начинаем изменять х2, давая ему приращения Н2 или –Н2 (точки 7, 8, 9, 10 ).

Затем снова движемся вдоль оси х1 (точки 11, 12, 13 ), снова меняем направление (точки 14, 15 ) и т. д. На рис. 7.8 изображена ситуация, когда из точки 12 двигаться некуда: во всех окружающих точках (9, 13, 14, 15 ) значение F меньше, чем в данной. Это значит, что мы уже приблизились к максимуму и прежние крупные шаги из точки 12 переносят нас через него. Поэтому уменьшаем шаги (например, вдвое – см. точку 16 ) и продолжаем поиск уменьшенными шагами.

Уменьшение шага может производиться неоднократно. Но в тот момент, когда эти шаги оказываются меньше, чем соответственно ε1 и ε2, логично считать, что максимум зафиксирован достаточно точно и можно закончить расчет, приняв лучшую точку за оптимум.

Если факторов больше двух, то после движения вдоль осей х1 и х2 производится движение вдоль осей х3, х4 и т. д. и лишь затем снова начинается движение вдоль х1. В описанном варианте движение вдоль каждой оси осуществляется так же, как при сканировании.

Если нужна большая точность определения оптимальных значений xi, можно поступать и по-иному: например, организовывать такое движение, как поиск методом золотого сечения.

Метод градиента (Ньютона-Рафсона, крутого восхождения-спуска). Численные частные производные. Ход процесса. Управление шагом поиска. Правило останова.

Метод градиента. Существует много вариантов этого метода.

Рассмотрим простейший из них. Подробно опишу также лишь случай двух факторов.

Как и в методе покоординатного спуска, вначале выберем координаты исходной точки х1Н и х2Н , шаги H1 и Н2 и малые приращения ε1 и ε2. Движение к оптимуму начнем не вдоль какой-либо оси координат, а в направлении градиента (если ищем минимум, то в противоположном градиенту направлении). Поскольку Н1 и Н2 приняты за единичные приращения координат, формула градиента получит вид (полужирный шрифт означает, что выделенные величины – векторы, и сложение ведется как векторное):

Ясно, что для расчета направления градиента необходимо знать частные производные целевой функции по факторам. Для расчета производных проводится вспомогательная серия расчетов (см. рис. 7.9). Около начальной точки 1 ставятся две вспомогательные точки: 1' на расстоянии ε1 вдоль оси х1 и 1'' на расстоянии ε2 вдоль оси х2, и в них рассчитывается функция F. Производные находим по формулам

Дальше можно действовать по-разному. Можно определить производные в новой точке i + 1, найти новое направление градиента, сделать шаг и т. д. Но чаще поступают иначе. Если шаг оказался удачным, т. е. если Fi+1 > Fi (при поиске максимума), то делают следующий шаг в том же направлении, подставляя в формулу (7.29) ранее найденные значения производных. Практически наверняка это будет уже не направление градиента: его направление в разных точках пространства факторов – разное, если только функция F не

является линейной. Но можно надеяться, что еще один шаг в прежнем направлении снова даст приращение F нужного знака, хотя и не максимально возможное (так как от градиента мы отклонились). Зато мы сэкономим на том, что не будем лишний раз рассчитывать производные. Если и этот шаг удачен, шагнем еще раз и т. д.

Рис. 7.9. Схема расчетов в методе градиента

Рис. 7.10. Схема расчета после неудачного шага

Что делать, когда шаг неудачен? Очевидно, поверхность настолько искривлена, что данное направление перестало вести нас вверх, мы «перескочили» через ту окрестность предыдущей точки, в которой функция возрастала. Поэтому в таком случае обычно уменьшают шаг, например вдвое. Теперь, если уменьшенный шаг в том же направлении будет удачен, нет смысла делать еще шаг, поскольку он приведет в «плохую» точку (см. рис. 7.10, а : крестик – неудачный шаг, (i + 2) – точка половинного шага). В этом случае около точки (i + 2) поставим вспомогательные точки для расчета производных по формуле (7.27), найдем новое направление градиента и двинемся по нему (на рис. 7.10 вспомогательные точки – черные кружки, новое направление градиента – стрелка). Если же и уменьшенный шаг не приведет в «хорошую» точку (рис. 7.10, б), то вернемся в точку i и будем в ней искать направление градиента.

Движение продолжаем до тех пор, пока шаги не станут очень малыми. Уменьшение шагов объясняется двумя причинами: первая – неоднократным уменьшением в тех случаях, когда большой шаг оказывался неудачным; вторая – это принципиально важнее, – то, что вблизи оптимума производные близки к нулю и формула (7.29) дает уже очень малые приращения.

Для останова вычислений можно использовать момент, когда оба приращения Δxij окажутся меньше, чем соответствующие малые величины εj.

Метод Розенброка. Форма поверхности отклика целевой функции приближенно моделируется зависимостью второго порядка по факторам (параболоидом). Ход процесса. Управление шагом поиска. Правило останова.*под большим вопросов

Метод вращающихся координат (метод Розенброка). Суть метода состоит во вращении системы координат в соответствии с изменением скорости убывания целевой функции. Новые направления координатных осей определяются таким образом, чтобы одна из них соответствовала направлению наиболее быстрого убывания целевой функции, а остальные находятся из условия ортогональности. Идея метода состоит в следующем (рис. 7.6).

Из начальной точки х[0] осуществляют спуск в точку х[1] по направлениям, параллельным координатным осям. На следующей итерации одна из осей должна проходить в направлении y1 = х[1] - х[0], а другая - в направлении, перпендикулярном к у1. Спуск вдоль этих осей приводит в точку х[2] , что дает возможность построить новый вектор х[2] - х[1] и на его базе новую систему направлений поиска. В общем случае данный метод эффективен при минимизации овражных функций, так как результирующее направление поиска стремится расположиться вдоль оси оврага.

Алгоритм метода вращающихся координат состоит в следующем.

1. Обозначают через р1[k], ..., рn[k] направления координатных осей в некоторой точке х[k] (на к-й итерации). Выполняют пробный шаг h1 вдоль оси р1[k], т. е.

x[kl] = x[k] + h1p1[k].

Если при этом f(x[kl]) < f(x[k]), то шаг h умножают на величину α > 1;

Если f(x[kl]) > f(x[k]), - то на величину (-α), 0 < | α | < 1;

x[kl] = x[k] + α h1p1[k].

Полагая h1 = а1 .получают x[kl] = x[k] + a1p1[k].

2. Из точки х[k1] выполняют шаг h2 вдоль оси р2[k]:

x[k2] = x[k] + a1p1[k] + h2p2[k].

Повторяют операцию п. 1, т. е.

x[k2] =x[k] + а1р1[k] +а2p2[k].

Эту процедуру выполняют для всех остальных координатных осей. На последнем шаге получают точку

х[kn] = х[k+1] = х[k] + 

3. Выбирают новые оси координат p1[k+1], …, рn[k+1]. В качестве первой оси принимается вектор

р1[k+1] = x[k+l] - x[k].

Остальные оси строят ортогональными к первой оси с помощью процедуры ортогонализации Грама - Шмидта. Повторяют вычисления с п. 1 до удовлетворения условий сходимости.

Коэффициенты α подбираются эмпирически. Хорошие результаты дают значения α = - 0,5 при неудачных пробах (f(x[ki]) > f(x[k])) и α = 3 при удачных пробах (f(x[ki]) < f(x[k])).

Метод Розенброка ориентирован на отыскание оптимальной точки в каждом направлении, а не просто на фиксированный сдвиг по всем направлениям. Величина шага в процессе поиска непрерывно изменяется в зависимости от рельефа поверхности уровня. Сочетание вращения координат с регулированием шага делает метод Розенброка эффективным при решении сложных задач оптимизации. Например, он эффективен для «овражных» функций, т.к. после спуска «на дно оврага» можно повернуть координаты и следовать к минимуму «по дну оврага». Такие «овражные» функции также получили название функции Розенброка. Функции этого типа часто используют для оценки эффективности различных методов отыскания экстремума.

Экспериментальный поиск оптимума. Влияние ошибок измерений на выбор шага поиска. Применение планов 1 и 2 порядка. Применение аппроксимации полиномами.

Наиболее сложен для оптимизации случай, когда мы не знаем вида целевой функции. В этом случае единственная возможность – находить оптимум экспериментально.

В принципе здесь можно применять любой из рассмотренных методов (дитохомия, золотое сечение), но при этом приходится учитывать ряд дополнительных обстоятельств.

Во-первых, вследствие наличия случайных ошибок опытные точки нельзя располагать слишком близко одну к другой. В противном случае значения критерия оптимальности, полученные в соседних точках, окажутся неразличимыми: различия в величине критерия (малые, потому что точки близки) будут значительно меньше уровня ошибки, вследствие чего не удастся опровергнуть гипотезу о равенстве этих значений.

Во-вторых, в эксперименте гораздо острее, чем в расчете, стоит проблема эффективности поиска. Эксперимент почти всегда дороже, чем единичный расчет целевой функции. Расчетная задача, где придется 1000 раз рассчитать F, может оказаться не очень большой

по объему. Эксперимент же по отыскиванию оптимума, требующий 100 опытов, уже очень велик.

В-третьих, при экспериментальной оптимизации характер зависимости F от факторов, как правило, бывает проще, чем при расчетной. Это объясняется тем, что ошибки опытов «сглаживают рельеф» целевой функции. Таким образом, в эксперименте обычно можно

работать с простейшими математическими моделями – чаще всего с многочленами 1-го или 2-го порядков.

Применительно к планированию эксперимента метод покоординатного спуска обычно называют методом Гаусса – Зайделя. Его главное преимущество – простота. Каждое движение (сканирование) вдоль одной из осей координат означает, что от опыта к опыту изменяется только один фактор и влияние этого фактора получается в ясной форме однофакторной зависимости. Его недостаток – малая эффективность, присущая однофакторному планированию эксперимента (см. разд. 2.4). Поэтому методом Гаусса – Зайделя в эксперименте пользуются не часто.

Казалось бы, отмеченная выше простота математических моделей, встречающихся в экспериментальной оптимизации, открывает еще одну возможность. Опишем целевую функцию многочленом. Ясно, что многочлен 1-й степени не может описать зависимость,

имеющую экстремум. Более того, и добавление взаимодействий не позволяет этого сделать. Тогда используем многочлен 2-й степени. Реализуем в интересующей нас области план 2-го порядка. Получив оценки параметров многочлена, легко определить экстремум на основе уравнений (7.5). Однако такой способ отыскания экстремума

крайне неточнен.

Исходная область пространства факторов всегда достаточно велика, и в этой большой области описание целевой функции многочленом 2-го порядка неадекватно, поскольку этот многочлен – лишь приближенное представление неизвестной нам «истинной» функции. Кроме того, экспериментальные точки в этом случае располагаются нерационально: в большинстве своем они попадают в части области, далекие от экстремума и поэтому неинтересные для исследователя.

Понятие об идентифицируемости как возможности определения искомых параметров модели и характеристик полученных оценок: однозначности и точности.

Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. 

Метод Бокса –Уилсона. (на всякий случай) Он состоит в следующем. Сначала ставится одна или несколько серий опытов, цель которых – приблизиться к оптимуму по градиенту функции, а затем вблизи экстремума ставится план 2-го порядка и оптимум отыскивают так, как описано выше.

В планировании эксперимента градиентный метод движения к оптимуму называют крутым восхождением. Отличия от метода, описанного в разд. 7.3, обусловлены ошибками опытов. По этой причине нельзя находить частные производные так, как там указано: в формулах (7.27) приращения ε должны быть малы; при малых расстояниях между точками слишком сильно скажутся ошибки опытов и оценка направления градиента будет очень сильно отклоняться от истинного направления.

Поэтому поступим так. Вокруг исходной точки как центра построим факторный эксперимент 2р или дробный факторный эксперимент. Зависимость отклика от факторов опишем многочленом 1-й степени (в дальнейшем, как и в разд. 2.4, будем обозначать критерий оптимальности, он же отклик, буквой у):

Тогда частные производные равны соответствующим коэффициентам регрессии:

С учетом этого, а также того, что за единичный шаг в направлении каждой оси uj (uj выражено в размерных, некодированных, так называемых натуральных единицах) естественно принять интервал варьирования δj , формула (7.29) примет вид

Здесь m – множитель, регулирующий длину шага: шаг должен быть не слишком мал, иначе движение будет очень медленным, но и не слишком велик, а то можно быстро уйти в область, где направление градиента совсем иное. Удачный выбор значения m обычно связан с достаточным опытом в применении метода. В качестве разумной, хотя зачастую и не самой лучшей, могу рекомендовать такую оценку:

Выражение в знаменателе – наибольшая из абсолютных величин коэффициентов регрессии, за исключением свободного члена. В таком случае шаг по оси наиболее сильно влияющего фактора равен интервалу варьирования, по остальным – соответственно меньше.

Отмечу еще одну особенность расчета по уравнению (7.32). Не следует стремиться получать значения приращений факторов со слишком большой точностью. Наоборот, значения, найденные по формуле (7.32), желательно округлять так, чтобы в опытах задавались удобные значения факторов. Нецелесообразно изменять от опыта к опыту температуру на 4,263°, куда удобнее – на 4,25° или даже на 4°. Дело в том, что направление градиента очень чувствительно к значениям принимаемых при построении плана интервалов варьирования. Но мы реально всегда задаем эти интервалы не на

основе серьезной теории, а весьма приблизительно – обычно ориентируясь на привычные круглые значения. Практически никогда мы не можем утверждать, что интервал варьирования температуры 10° с точки зрения какой-то теории лучше, чем интервал 11,18°. Но расчет по формуле (7.33) даст при принятии этих интервалов существенно разные значения. Поэтому, если мы округляем шаги по осям в крутом восхождении, у нас нет никаких причин думать, что мы замедляем (равно как и ускоряем) движение к экстремуму.

Движение по направлению крутого восхождения продолжается до тех пор, пока у возрастает (либо убывает, если мы ищем минимум). После этого либо ставят новый факторный эксперимент и находят новое направление градиента, либо переходят к плану 2-го порядка, как было рассказано выше.