4. Модели неидеальных потоков

Параметры моделей. Неидеальное через идеальное как метод моделирования неидеальных потоков.

Параметры модели. Чаще всего простота или сложность математической модели связаны с тем, сколько в нее входит параметров – коэффициентов, учитывающих те или иные особенности объекта. Значения параметров характеризуют свойства данного конкретного объекта, отличающие его от других объектов того же класса. Чем больше параметров входит в модель, тем подробнее удается охарактеризовать его и тем точнее описать. На одном полюсе здесь выступают предельно идеализированные модели, такие, как идеальный газ, абсолютно упругое тело и др.

Уравнения при этом либо вообще не содержат параметров, включая лишь универсальные константы (идеальный газ), либо их число минимальное (модуль упругости в законе Гука). Эти идеализированные модели почти полностью игнорируют конкретные свойства объектов. На другом полюсе — сложные многопараметрические модели, учитывающие много конкретных свойств. Так как мы всегда хотим иметь максимально точное описание объекта, с этой точки зрения сложные модели обладают несомненными преимуществами.

Но у сложных моделей есть и недостатки. Прежде всего такую модель трудно обрабатывать. Если данная модель входит как составная часть в сложные модели более высоких иерархических уровней, то в конце концов может получиться такое громоздкое описание, что его не удастся обсчитать. К тому же, чем сложнее зависимость, тем труднее представить себе, как она выглядит в целом. Хотя такая наглядность, возможность составить общее представление о характере зависимости не обязательно нужна при моделировании, но обычно она заметно облегчает анализ. Еще одна трудность, связанная с применением многопараметрических моделей, — это чувствительность к ошибкам опытов. Чем больше параметров, тем более точный эксперимент требуется, чтобы достаточно хорошо оценить эти параметры. Если модель построена на основе структурного подхода, а эксперимент не очень точен, то возникает специфическая опасность потери физического смысла: можно получить неверные значения параметров, хотя модель в целом будет давать приемлемое совпадение с опытными данными. Это происходит потому, что ошибки в значениях разных параметров взаимно компенсируются. Модель остается пригодной для количественного описания объекта (в достаточно узких пределах), но физический смысл искажается — мы получаем превратное представление о величинах эффектов, связанных с параметрами. В конце концов физический смысл теряется и параметры модели получают смысл подгоночных параметров, назначение которых — лишь привести в соответствие данные и модель. Уравнение становится эмпирическим, о чем исследователь может не знать. Проиллюстрировать это можно даже на примере достаточно простого двухпараметрического уравнения Ван-дер-Ваальса.

Простейшие модели. Ячеечная модель.

Ячеечная модель – простейшая однопараметрическая модель.

Эта модель схематически представляет реальный аппарат как некоторое число п одинаковых последовательно соединенных аппаратов (ячеек) идеального смешения (рис. 4.18). Суммарный объем всех ячеек равен объему реального аппарата, следовательно, объем каждой ячейки равен Va/n (Общий объем поделен на n (один параметр) равных последовательных объемов ИС.) Число ячеек – единственный параметр ячеечной модели.

В ряде случаев в аппарате действительно можно выделить участки по ходу потока, в каждом из которых жидкость более или менее полно перемешивается.

Системы, близкие к ячеечной модели.

Схема ячеечной модели близка, например, к картине движения жидкости через каскад реакторов с мешалками или через тарельчатую барботажную колонну провального типа, в которой жидкость интенсивно перемешивается на каждой тарелке и быстро переливается с тарелки на тарелку. В других потоках отождествить физическую картину с ячеечной моделью можно лишь ценой значительных упрощений. Например, для турбулентного потока в первом приближении можно считать, что каждая частица проходит некоторое расстояние как единое целое, а затем перемешивается с окружающим частицами. Участок, на котором происходит это перемешивание (путь смешения), можно, хотя и весьма грубо, сопоставить с ячейкой смешения. Другой такой пример – течение газа в зернистом слое. Выходя из узкой щели между зернами в более широкую полость (такие всегда есть в слое), газ завихряется и перемешивается, в результате чего возникает картина чередующихся перетеканий и перемешиваний. Но и здесь схема ячеечной модели сильно огрубляет реальное явление. Однако в ряде случаев ошибка огрубления несущественна для решения конкретной задачи, а простота модели делает ее применение желательным

Дифференциальная функция распределения по временам пребывания ДФРВП вида C()=nⁿ^n-1e^-n/(n-1)!. n=1, n=∞. ²()=1/n как оценка n. Поведение при n=∞!!! Концентрация реагента от времени пребывания для ИВ, ИС и ЯМ (n=3). Выход i-1 как вход i. n уравнений. Решать последовательно. Для конечной концентрации реагента реакции первого порядка C_An=C_A0/(1+kt/n)ⁿ

Рассмотрим распределение времени пребывания и изменение концентрации по длине аппарата для ячеечной модели. Дифференциальная функция распределения времени пребывания имеет вид (формула приводится без вывода)

График этой функции изображен на рис. 4.19. По мере увеличения числа ячеек кривые становятся все более крутыми, приближаясь к графику δ-функции. При п = 1 формула (4.85) переходит в уравнение (4.78), а при п→∞ – в (4.74).

Таким образом, потоки идеального смешения и идеального вытеснения являются крайними случаями ячеечной модели.

Разумеется, физическая схема, включающая 0,77 ячейки смешения, не имеет смысла. Приходится полагать, что параметр n содержит эмпирическую поправку. Впрочем, и в тех случаях, когда число ячеек связано с совершенно определенным числом конструктивных элементов (например, тарелок колонны), эксперимент по изучению распределения времени пребывания, как правило, дает значение n, отличное от этого числа и чаще всего не целое. Различие объясняется отклонением течения на каждой ступени от идеального, а также случайными ошибками эксперимента. Поэтому n и здесь содержит эмпирическую поправку. В некоторых расчетах удается использовать нецелое n, в других – параметр округляют. Распределение концентрации реагента по длине аппарата показано на рис. 4.20. Для последней ячейки концентрация вещества А в ячеечной модели совпадает с его концентрацией при идеальном смешении. Но первые ячейки работают при бóльших сА и соответственно при бóльших скоростях реакции. С этой точки зрения ячеечная модель занимает промежуточное место между обеими моделями идеальных потоков.

Рис. 4.20. Распределение концентрации реагента по длине аппарата: 1 – идеального вытеснения; 2 – идеального смешения; 3 – состоящего из трех ячеек.

Рис. 4.21. Схема аппарата из трех ячеек.

Рассмотрим теперь протекание химической реакции в ячеечной модели. Описание этого процесса есть просто описание процесса при идеальном смешении, повторенное n раз. Выходные значения концентрации и температуры i-й ячейки являются входными для (I + 1)-й. Для реакции А → В это показано на рис. 4.21. Для i-й ячейки уравнение баланса по веществу J в стационарном режиме имеет вид

Для конверсии =1-1/(1+kt/n)ⁿ. Среднее время! Крайние случаи. Дробное n.

Секционирование, перегородки.

Пример 4.11 показывает, что с увеличением числа ячеек степень превращения довольно быстро приближается к результатам, характерным для идеального вытеснения. Ясно, почему в технологии часто применяется прием секционирования: аппараты, в которых создается интенсивное смешение потока жидкости, делят на последовательные секции, между которыми она перетекает по возможности без смешения. Для этого обычно служат всякого рода перфорированные перегородки. Иногда для достижения того же эффекта применяют каскады последовательно соединенных аппаратов с мешалками. Кроме увеличения степени превращения секционирование влияет и на другие показатели процесса, в частности на селективность.

Селективность. Уже три ячейки эффективны! Особо – при порядке 0!

Таким образом, и в этом случае несомненна целесообразность секционирования аппарата: растет как степень превращения, так и селективность.

Динамика, чувствительность, управляемость, устойчивость. Параметрическая чувствительность и управляемость. Разница и сходство.

Процессы в динамике (меняющиеся во времени) также играют в химической технологии большую роль. К ним относятся все периодические процессы, а также такие важные этапы любого процесса, как пуск и остановка, и переходные процессы, возникающие при изменениях режима работы вследствие либо случайных возмущений, либо регулирующих воздействий. Математическое описание нестационарного процесса обязательно содержит производные по времени. В простейшем случае это связано с членами, описывающими накопление. Поэтому математический аппарат, применяемый для описания и анализа этих процессов, – дифференциальные уравнения. Методы анализа результатов на основе дифференциальных уравнений, например метод Лапласа [13]. Рассмотрим простейшие случаи – переходные процессы в идеальных аппаратах при ступенчатом возмущении по концентрации. Такой тип возмущения часто анализируется в теории: до некоторого момента t = 0 величина на входе имела одно значение, а затем мгновенным скачком принимает новое значение, которое сохраняется в дальнейшем. Пример подобного возмущения (по концентрации индикатора) показан на рис. 4.12,а.

Рассмотрим протекание необратимой реакции 1-го порядка А → В в аппарате идеального смешения. Температура и расход жидкости постоянны. До момента t = 0 концентрация вещества А на входе составляла c01, затем она скачком возросла до c02. Математическое описание процесса состоит из одного уравнения баланса, являющегося частным случаем уравнения (4.34):

Это и есть уравнение нашего переходного процесса, которое описывает изменение концентрации на выходе из аппарата, графически показанное на рис. 6.1,б.

Рис. 6.1. График переходного процесса в аппарате идеального смешения: а – на входе; б – на выходе

График – экспонента, начинающаяся от первого стационарного значения и асимптотически приближающаяся ко второму. Объект, описываемый уравнением (6.1) или соответственно (6.4), в теории автоматического регулирования называют апериодическим звеном 1-го порядка. Постоянная времени в данном случае составляет .

По-иному выглядит переходный процесс в аппарате идеального вытеснения. В стационарном режиме при cA0 = c01 концентрация вещества А на выходе аппарата определяется формулой (4.14):

Если на входе происходит возмущение, то вначале оно никак не проявляется на выходе – те порции жидкости, в которых начальная концентрация изменилась, до выхода еще не дошли. Когда же пройдет время, равное t , концентрация скачком изменится до

(рис. 6.2).

Рис. 6.2. График переходного процесса в аппарате идеального вытеснения: 1 – на входе; 2 – на выходе

С точки зрения теории автоматического регулирования в аппарате идеального вытеснения имеет место чистое запаздывание (транспортное запаздывание).

В ряде случаев анализ математической модели позволяет обнаружить такие особенности процесса, предсказание которых по лабораторным данным невозможно или весьма затруднительно, поскольку они сильно зависят от размеров объекта. Рассмотрим две такие особенности.

Параметрическая чувствительность Пij – производная от i-й выходной величины по j-му входному параметру:

Чем больше Пij , тем сильнее влияет данный фактор на выход. Если параметрическая чувствительность очень мала, то соответствующим фактором нельзя пользоваться как управляющим: он почти не влияет на процесс. Если параметрическая чувствительность чрезмерно велика, процесс становится трудноуправляемым. Даже малые колебания входного параметра приводят к резким колебаниям режима.

Поэтому приходится либо чрезвычайно точно стабилизировать вход, либо тем или иным способом снижать чувствительность. Отмечу, что поскольку Пij — функция входных факторов, то при их изменении процесс может попадать в области и малой, и высокой

чувствительности.

Пример 6.1. Рассчитано протекание необратимой экзотермической реакции 1-го порядка А → В в аппарате идеального вытеснения с охлаждаемой стенкой [38]. Исследовано влияние температуры стенки Тп (постоянной по длине аппарата) на температуру в горячей точке – наибольшую температуру в зоне реакции. Математической моделью процесса являются уравнения (4.5), (3.53) и (5.28). Результаты моделирования показаны на рис. 6.3.

Рис. 6.3. График чувствительности трубчатого реактора к температуре стенки

По оси абсцисс отложено время реакции (начиная от момента входа смеси в аппарат), по оси ординат – температура смеси. До Тп = 335 К параметрическая чувствительность невелика. Это объясняется тем, что входящая смесь охлаждается и реакция идет очень медленно. Но затем при росте Тп начинается бурное развитие реакции, самоускоряющейся за счет выделения тепла. Увеличение Тп на 2,5 К (от 335 до 337,5 К) вызывает рост температуры в горячей точке почти на 70 К. Отсюда находим, что П ≈ 70 : 2,5 = 28.

Если в рассмотренном случае использовать изменяющуюся по длине температуру стенки (вначале значение Тп относительно велико, а затем оно снижается), то скачок температуры сгладится и П понизится. Управлять процессом будет легче.

Заметим, что в ряде случаев параметрическую чувствительность целесообразно определять так, как это сделано в примере 6.1: заменяя в уравнении (6.5) производную отношением малых конечных приращений

Предельный случай параметрической чувствительности: П → ∞. Это означает, что бесконечно малое изменение входного параметра вызывает конечное изменение показателей работы. Такая ситуация наблюдается при неустойчивости процессов.

Флуктуации и возмущающие воздействия. Связь. Устойчивость стационарных режимов в ХТ.

Устойчивость химических процессов определяется их реакцией на возмущающие воздействия. Если процесс, проходящий устойчиво, отклонить от данного состояния, а затем предоставить самому себе, то он самопроизвольно вернется в начальное состояние.

Наиболее известно явление устойчивости равновесия механических систем. Так, стул, стоящий на четырех ножках, устойчив. Если его слегка наклонить, а затем отпустить, то он вновь станет на ножки. Устойчив также стул, лежащий на боку. Теоретически можно уравновесить стул и на двух ножках, и даже на одной. И если бы он не испытывал никаких толчков, то простоял бы в таком положении неопределенно долго. Но

достаточно легкой вибрации пола – и стул, отклонившись от положения равновесия, уже не вернется к нему, а будет отклоняться дальше, пока не встанет на четыре ножки или не упадет на бок. Равновесие стула, стоящего на одной или двух ножках, неустойчиво.

Если систему, находящуюся в неустойчивом равновесии, вывести из него, а затем предоставить самой себе, то она будет самопроизвольно продолжать отклоняться от исходного состояния. Вопрос о том, что может произойти с ней дальше, я вкратце рассмотрю немного ниже. Из примера со стулом ясно, что одна из возможностей

(возникающая, пожалуй, чаще всего) – приход к какому-либо устойчивому равновесию.

В химической технологии обычно анализируют устойчивость стационарных режимов работы. В любом технологическом процессе стационарный режим подвержен случайным колебаниям (возмущениям). Предположим, что в результате возмущения значение какого-то входного параметра х, влияющего на работу аппарата, слегка отклонилось от постоянной величины (рис. 6.4,а) и затем вернулось к начальному положению. Как будет вести себя аппарат, находящийся в устойчивом и в неустойчивом состояниях?

О работе аппарата будем судить по изменению во времени значения какого-либо из выходов системы у. Если исходный режим устойчив, то переходный процесс будет проходить приблизительно так, как показано на рис. 6.4,б, – через некоторое время после снятия возмущения режим вернется к начальному состоянию. Если же состояние аппарата было неустойчивым, то при том же характере возмущения по окончании переходного процесса аппарат окажется уже в каком-либо другом, устойчивом состоянии (рис. 6.4,в).

Рис. 6.4. Графики возмущающего воздействия (а) и переходных процессов при устойчивом (б) и неустойчивом (в) режимах

Необратимая экзотермическая реакция первого порядка в потоке ИС с отводом тепла. Скорость r=kC_A0/(1+kt)=Ae^-E/RTC_A0/(1+Ae^-E/RTt). При низкой т-ре Ae^-E/RTC_A0, при высокой C_A0/t (смысл!).

Рассмотрим задачу об устойчивости химических процессов на примере тепловой устойчивости экзотермической необратимой реакции 1-го порядка, протекающей в аппарате идеального смешения с отводом тепла. Для анализа этого случая нам потребуется зависимость скорости реакции, протекающей в аппарате идеального смешения, от температуры. Поэтому вначале найдем эту зависимость. Имеем необратимую реакцию 1-го порядка А → В, протекающую в аппарате идеального смешения. Скорость реакции выражается формулой

Рис. 6.5. Температурная зависимость скорости реакции в аппарате идеального смешения

Вначале зависимость (6.8) может показаться парадоксальной. Почему скорость реакции зависит не от концентрации в зоне реакции (которая при высокой температуре очень мала), а от концентрации реагента на входе в аппарат? Почему на скорость влияет среднее время пребывания? Учет особенностей процесса делает, однако, физический смысл такой зависимости достаточно ясным. При высоких температурах реакция протекает быстро, поэтому перерабатывается практически все вещество, вводимое в аппарат. Скорость реакции определяется просто количеством реагента, вводимого в аппарат в единицу времени (отсюда множитель cA0 в числителе формулы (6.8)), а также средним временем, затрачиваемым на переработку. Для анализа важно то, что в этом режиме скорость r не зависит от температуры: с ростом Т увеличивается k и одновременно уменьшается сА, но так как концентрация А на выходе очень мала, ее дальнейшее уменьшение практически не сказывается на разности (сА0 – сА) и соответственно на скорости реакции.

Теперь перейдем к анализу устойчивости данной реакции. Реакция протекает в аппарате идеального смешения. Тепло реакции отводится через поверхность Fт к теплоносителю, имеющему температуру Tтн.

Баланс Q₁=Q₂, где 1 от реакции, 2 отвод потоком и стенкой. V_aQ_pr=vC_T(T-T₀)+K_TF_T(T-T_TH). Перегруппировка. Вид функций. Максимально 3 корня, 3 стационарных состояния. Возмущение температуры. Устойчивость 1 и 3.

Если процесс стационарен, то его характеризует уравнение теплового баланса, которое запишем в виде

Обозначим левую часть уравнения через Q1, а правую – через Q2. Здесь Q1 – выделение тепла, т. е. количество тепла, выделяемого реакцией в единицу времени; Q2 – отвод тепла, т. е. количество тепла, выводимого в единицу времени с потоком и через стенку (за вычетом входящего с потоком). Итак, в стационарном режиме Q1 = Q2. (6.10) Если Q1 ≠ Q2, процесс нестационарен: при Q1 > Q2 температура растет во времени – система нагревается; при Q1 < Q2 система охлаждается. Исследуем, как зависят левая и правая части уравнений (6.9) – (6.10) от температуры в аппарате. В левой части VaQp – коэффициент, почти не зависящий от Т, так что функция Q1(Т) имеет такой же вид, как функция r (Т), изображенная на рис. 6.5, отличаясь лишь постоянным множителем. Правую часть уравнения (6.9) преобразуем, выделив скобками величины, не зависящие или почти не зависящие от T:

Таким образом, это практически линейная зависимость, причем Q2 растет с повышением Т. На рис. 6.9 зависимости Q1 и Q2 от Т представлены графически. Линия I выделения тепла и линия II отвода тепла пересекаются в трех точках 1, 2 и 3 при температурах Т1, Т2 и T3. При этих температурах соблюдается условие (6.10) и процесс стационарен. Итак, в данной ситуации при одних и тех же значениях всех внешних (входных) параметров возможны три различных стационарных режима. Рассмотрим вначале стационарный режим при температуре Т1. Так как скорости выделения и отвода тепла равны одна другой, то пока температура не меняется, режим остается стационарным. Предположим теперь, что в результате случайного возмущения температура в реакторе немного повысилась и стала равной T1 + dT (рис. 6.6). При этом из-за ускорения реакции возрастает скорость выделения тепла; этот рост происходит в соответствии с кривой тепловыделения. Одновременно из-за увеличения разности температур между реактором

Рис. 6.6. Зависимости выделения и отвода тепла от температуры в реакторе

и теплоносителем повышается скорость отвода тепла. Этот рост характеризуется прямой теплоотвода.

В точке 1 прямая идет круче кривой, поэтому при температуре T1 + dT скорость отвода тепла окажется выше, чем скорость его выделения. Раз так, то после снятия возмущения реактор начнет охлаждаться. Охлаждение будет продолжаться до тех пор, пока реактор не вернется к температуре Т1. При этой температуре скорости выделения и отвода тепла опять уравняются и режим снова станет стационарным. Наоборот, если в результате возмущения реактор слегка охладится, то скорость выделения тепла станет больше, чем скорость его отвода и реактор начнет нагреваться, пока снова не достигнет Т1. Таким образом, при температуре Т1 режим устойчив. При температуре Т3 с точки зрения устойчивости картина полностью аналогична предыдущему режиму. Прямая теплоотвода также идет круче, чем кривая выделения тепла. Точно такие же рассуждения приводят к такому же выводу: режим устойчив. Теперь обратимся к точке 2. Здесь наклон прямой теплоотвода меньше, чем наклон кривой выделения тепла. Так же, как и в точках 1 и 3, Q1 = Q2, и если нет возмущений, режим будет оставаться стационарным. Но предположим, что произошло случайное возмущение – повышение температуры до T2 + dT. При этой температуре скорость выделения тепла станет большей, чем скорость теплоотвода. После снятия возмущения реактор будет не охлаждаться, а нагреваться, удаляясь от начального состояния. Нагревание будет продолжаться до тех пор, пока при температуре T3 реактор не придет в устойчивое стационарное состояние. Точно так же при случайном охлаждении реактор будет самопроизвольно охлаждаться до тех пор, пока не дойдет до устойчивого состояния при Т1. Итак, из трех возможных в данных условиях стационарных режимов два – при низкой температуре (и малой скорости реакции) и при высокой

температуре (и большой скорости реакции) – устойчивы, а третье – при промежуточных температуре и скорости реакции – неустойчиво.

Условие dQ₂/dT>dQ₁/dT. Отличие около состояния 2 как неустойчивого. Автоматика или интенсификация отвода тепла у точки 2 как модератор системы. Иначе C_T/t+K_TF_T/V_a>Q_pdr/dT, где F_T/V_a=f_T – удельная поверхность, падает с ростом объема. Условие устойчивости в этой задаче состоит в том, что прямая теплоотвода идет круче, чем прямая тепловыделения. Это условие можно записать формулой

Что делать, если желательно работать в области температур вблизи T2? Есть два выхода: один – построить систему автоматического регулирования, которая будет удерживать режим в неустойчивом состоянии, второй – сделать теплоотвод столь интенсивным, что линия отвода тепла будет всюду круче линии выделения, как это показано на рис. 6.7.

Рис. 6.7. Зависимости Q1 и Q2 от Т при устойчивости во всем диапазоне Т

Подставив в формулу (6.12) выражения для Q1 и Q2 из (6.9), после несложных преобразований получим условие устойчивости в виде

Коллизия размера и устойчивости. Заметим, что левая часть будет большой при условии интенсивного теплообмена, т.е. когда велики Кт и удельная поверхность fт = Fт / Va. Это указывает путь к повышению устойчивости. Но одновременно учтем следующее. Если размер аппарата уменьшается, то величина fт растет. Поэтому условия работы малой модели могут соответствовать зависимости, показанной на рис. 6.7, при этом неустойчивость не возникает. При переходе к большим размерам установки fт уменьшается и возможно неожиданное возникновение неустойчивости. В серьезных технологических разработках необходимо анализировать параметрическую чувствительность и устойчивость методами математического моделирования.

Подобие с зерном непористого катализатора. Рост температуры в ядре потока – перенос прямой вправо до касания (неустойчивость).

Зажигание катализатора. Падение температуры – перенос влево до касания (неустойчивость). Погасание катализатора при более низкой т-ре, чем зажигание.

Зажигание катализатора. Зависимость скорости реакции на непористом катализаторе от температуры поверхности, близка к зависимости, показанной на рис. 6.5. В случае экзотермической реакции выделяющееся тепло отводится в поток газа или жидкости. Уравнение (5.70), так же как и баланс (6.9), сводится к записи Q1 = Q2. При этом изменение температуры в ядре потока Тя вызывает на графике параллельный перенос прямой теплоотвода: чем выше Тя, тем правее пройдет эта прямая (рис. 6.8).

Рассмотрим с помощью этого рисунка процесс постепенного повышения Тя. Пока эта температура растет от Т1 до Т5, процесс на зерне устойчиво удерживается в кинетической области (пересечение прямых с нижней частью кривой выделения тепла). При достижении в ядре потока температуры Т5 произойдут скачкообразный рост температуры Тп и переход в диффузионную область – зажигание катализатора. Зажигание связано с потерей устойчивости низкотемпературного процесса: в точке, где прямая 5 касается кривой, процесс уже неустойчив. После зажигания устойчивым становится процесс, соответствующий верхней части кривой Q1. Он будет устойчив даже, если температура Тя начнет понижаться. Лишь при достижении в ядре температуры Т2 (прямая 2) устойчивость будет потеряна, температура скачком упадет, процесс перейдет в кинетическую область – произойдет погасание катализатора.

Гистерезис!

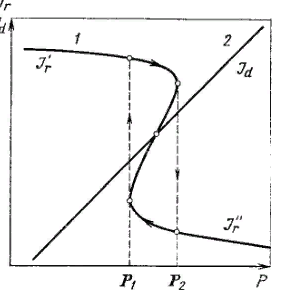
Прямая 2 на рис. 7.2.

Кинетическая и диффузионная область. Неустойчивость в изотермических режимах.

Проанализируем простой случай: процесс стационарен, проходит изотермически. Не углубляясь в механизм каталитической кинетики, будем считать, что реакция необратима, имеет 1-й порядок, а ее скорость

где cп – концентрация реагирующего вещества A непосредственно у поверхности. Для реакций не 1-го порядка закономерности качественно близки к тем, которые получаются в анализируемом случае.

Рассмотрим материальный баланс по реагенту А. В уравнении баланса присутствуют только два члена: вход и сток (уход и источник равны нулю – реагент не поступает с поверхности в поток и не образуется, так как реакция необратима; накопление тоже равно нулю ввиду стационарности). Окружим контуром малый участок каталитической поверхности, площадь которого примем за единицу; за интервал примем единицу времени (интервал конечен, так как процесс стационарен). Тогда вход А будет равен потоку вещества на поверхность, а сток – скорости гетерогенной реакции. Уравнение при этом принимает вид

Уравнение (5.44) выражает свойство аддитивности сопротивлений. Коэффициенты β, k и k′– скоростные коэффициенты: скорости процессов им пропорциональны. Обратные величины называют сопротивлениями. Формулу (5.44) можно прочесть так: общее со-

противление процессу 1/ k′ складывается из сопротивлений стадий: диффузионного 1/β и кинетического 1/k. Аддитивность сопротивлений говорит о том, что процесс складывается из последовательных стадий и что лимитировать будет медленная стадия.

Рассмотрим, от чего и как будет зависеть скорость процесса при наличии лимитирования. Здесь только необходимо учесть вот что. Из уравнения (5.39) следует, что скорость потока вещества А к поверхности равна скорости реакции. В этом смысле в стационарном случае нельзя говорить о медленной и быстрой стадиях – их скорости равны. Но сравнивать можно и по-другому: считая мерой скорости среднее время, затрачиваемое молекулой в одной стадии на преодоление пограничного слоя, а в другой – на химическое превращение после того, как она достигла поверхности. Тогда скорости становятся разными и их можно сравнивать.

Случай 1 : k << β, медленная реакция при быстром транспорте вещества к поверхности.

Каковы основные закономерности этого случая? Из вышесказанного ясно, что лимитирующая стадия – протекание химической реакции на поверхности. Реакция проходит в кинетической области.

Для уточнения особенностей этой области обратимся к уравнениям (5.38) – (5.44). Из (5.40) следует, что сп ≈ ся: быстрая диффузия выравнивает с_А по толщине пограничного слоя, медленная реакция «не в силах» существенно снизить эту концентрацию. Из (5.44) получим, что k′≈ k, так как малым слагаемым 1/β можно пренебречь по сравнению с большим 1/k. Теперь из (5.42) находим:

В уравнении (5.45) ничто не связано с процессом диффузии, все определяется через закономерности кинетики.

Случай 2 : k >> β, быстрая реакция при медленной диффузии.

Лимитирует подвод реагента через пограничный слой. Процесс идет в диффузионной области (внешнедиффузионной, диффузия проходит вне гранулы катализатора). Снова обратимся к уравнениям (5.38) – (5.44). Из (5.40) следует, что сп ≈ 0: знаменатель дроби много больше, чем числитель. Из (5.44) получим, что k′≈ β. Тогда уравнение (5.42)

можно записать в виде

Правую часть выражения (5.46) я записал так, чтобы было ясно: это уравнение массоотдачи для случая, когда концентрация со стороны твердой поверхности практически равна нулю.

Случай 3 : коэффициенты k и β сравнимы по величине. Ни одна из стадий не лимитирует процесса – он проходит в промежуточной (переходной) области. Скорость реакции рассчитывается по формуле (5.41).

Какие условия способствуют увеличению скорости массоотдачи? В первую очередь это рост скорости потока. В то же время скорость потока непосредственно не влияет на химическую кинетику.

Поэтому если процесс проходит в кинетической области, поток не влияет на его скорость; если в диффузионной, то увеличение скорости потока ускоряет процесс, а если в промежуточной, то при увеличении скорости потока процесс может перейти в кинетическую область.

Какие условия способствуют ускорению собственно реакции? Как уже говорилось, сильнее всего константа скорости реакции зависит от температуры. В то же время скорость массоотдачи слабо зависит от температуры, в особенности если движущая фаза – газ. В связи с этим кривая зависимости скорости реакции от температуры имеет

характерный вид (рис. 5.9).

В области низких температур общая скорость процесса сравнительно мала, но при этом с повышением температуры она резко возрастает в соответствии с уравнением Аррениуса. Процесс идет в кинетической области. При повышении температуры рост скорости процесса замедляется и начиная с некоторой температуры почти прекращается. Процесс вступает в диффузионную область.

Если увеличить скорость потока, т. е. снизить диффузионное торможение (верхняя кривая на рис. 5.9), то в кинетической области кривая пойдет точно так же, но промежуточная и диффузионная области начнутся при несколько более высоких температурах, а общая

скорость процесса в этих областях окажется выше.

Рис. 5.9. Зависимость скорости реакции от температуры для непористого катализатора.

Области: 1 – кинетическая; 2 – промежуточная; 3 – диффузионная

Общие проблемы науки (нелинейность, обратные связи).

Внешние связи системы. Определяя понятие «система», я уже говорил об исключительной важности связей между ее элементами. Для динамических систем не менее важны внешние связи – взаимодействия системы с окружающим ее миром. Внешние связи бывают двух основных классов: воздействия мира на систему – входы системы и воздействия системы на мир – ее выходы, результат функционирования системы. Особый случай – обратные связи: выход системы оказывает влияние на ее вход. Существуют положительные обратные связи, когда усиление выходного сигнала усиливает сигнал на входе, и отрицательные обратные связи, когда с усилением выходного сигнала входной ослабляется. Как правило, действие положительных обратных связей приводит к возбуждению системы, интенсификации ее деятельности; в неблагоприятных случаях это может привести к тому, что система «пойдет вразнос». Наоборот, отрицательные обратные связи стабилизируют состояние системы.

Фазовые координаты, аттракторы (узлы), репеллеры, седла, предельные циклы (перерегулирование, колебательные химические реакции). Странный аттрактор, хаос, турбулентность. Численное моделирование – проблема хаоса.

Некоторые особенности задач, связанных с устойчивостью.

При описании задач, связанных с устойчивостью, часто бывает удобно изображать состояние системы в фазовых координатах. По осям координат откладываются значения параметров, определяющих состояние системы. Точка в фазовом пространстве соответствует какому-либо из таких состояний.

При этом если мы рассматриваем изменение фазового графика во времени и если точка неподвижна, значит, состояние системы стационарно; нестационарный режим изображается движущейся точкой. Что отличает в фазовом пространстве неподвижные точки, соответствующие устойчивым или неустойчивым стационарным состояниям? Если состояние, изображаемое точкой, устойчиво, то около нее имеется область, в которой все возможные траектории нестационарных процессов движутся в направлении этой точки.

Переходные процессы заканчиваются стационарным состоянием. Такие точки называют аттракторами. Напротив, точку, изображающую неустойчивое стационарное состояние, окружает область, где все траектории направлены прочь от этой точки. Такую точку называют репеллером (от лат. attraho – притягивать, repello – отталкивать). Бывает и так, что малое число траекторий (обычно – две) направлены к данной точке, а остальные – от нее. Это случай седловой точки.

Что может произойти, если система вышла из неустойчивого состояния и предоставлена самой себе? Простейший вариант, к которому сводились рассмотренные выше случаи: вблизи данного репеллера отыщется аттрактор и точка перейдет в него, система окажется в ином, уже устойчивом состоянии. Но возможны и другие варианты.

Один из них таков. Точка начинает двигаться по замкнутой кривой, совершая один оборот за другим. Такую кривую называют предельным циклом. Движение точки по предельному циклу отображает протекание на объекте колебательного процесса, параметры которого периодически изменяются во времени. Так ведут себя многие процессы при перерегулировании: вместо того чтобы под воздействием регулятора прийти к заданному режиму, процесс начинает совершать непрерывные колебания [13]. То же наблюдается при возникновении колебательных химических реакций [39].

В последние десятилетия обнаруживается еще один возможный вариант, обозначаемый термином «странный аттрактор». Странный аттрактор – это не точка, а целая область в фазовом пространстве, обладающая двумя свойствами. Во-первых, это аттрактор – точка, попавшая в его окрестность, будет двигаться к нему и затем войдет внутрь. Во-вторых, внутри странного аттрактора существует множество (теоретически бесконечное) возможных траекторий, но все они неустойчивы. Точка, вошедшая в странный аттрактор, начнет двигаться по какой-либо траектории, но вследствие неустойчивости этого движения при малейшем возмущении перескочит на другую «случайно подвернувшуюся» траекторию, затем на третью и т.д. Система войдет в режим хаотических колебаний.

Пример 6.2. Ламинарное течение жидкости при постоянном расходе стационарно. Но если скорость превысит предел, определяемый критическим значением критерия Re, то ламинарное течение становится неустойчивым и поток эволюционирует в сторону странного аттрактора – турбулентного режима, в котором траектория движения любой частицы неустойчива и поэтому претерпевает хаотические пульсации.

Автокатализ и устойчивость. Затравка в биотехнологии. Проблемы экологии и устойчивость.

Устойчивость режимов при автокатализе. Рассмотрим еще одну задачу, представляющую заметный интерес для химиков. В аппарате идеального смешения при постоянных температуре и расходе жидкости проводится реакция

Таким образом, вещество В является и продуктом реакции, и катализатором. Такая схема реакции – простейшая модель процессов типа ферментации, протекающих под воздействием микроорганизмов (об этом я уже упоминал в разд. 4.2). В этом случае вещество А – субстрат, т.е. пища для бактерий или грибков; С – тот продукт, который следует получить; В – сами микроорганизмы. Они выступают в роли и катализатора, потому что без них реакция не идет, и продукта: поедая субстрат, они размножаются, и чем больше потреблено пищи, тем больше их образовалось. Существенная особенность процесса: сВ0 = 0. Это обусловлено тем, что входящий поток субстрата стерилизуют, поскольку иначе на вход могут попасть так называемые «дикие расы» микроорганизмов, бесплодные, но хорошо приспособленные к конкуренции и культурная раса В окажется вытесненной. Анализ, скорее всего, не нужен.

реакция не начнется, сколько бы ни продолжать продукты образовываться не будут. Второе решение относится к случаю, когда вначале в аппарате присутствовало вещество В (была введена затравка микроорганизмов), реакция началась и хотя в установившемся стационарном режиме катализатор не вводится он образуется в результате реакции и поддерживает ее протекание. Возникает вопрос об устойчивости: что произойдет, если концентрация вещества В случайно слегка изменится? Выправится в дальнейшем это изменение или окажется, что из аппарата выносится больше катализатора, чем образуется, и в конце переходного периода вещества В не останется, реакция прекратится и реализуется первое решение?

Рис. 6.9. Изменение концентрации вещества А в переходном процессе

Снова обратимся к уравнению (6.19). Правая его часть – это квадратный трехчлен относительно сА, причем член, содержащий квадрат, положителен. График зависимости представляет собой параболу с минимумом, находящимся между корнями трехчлена (рис. 6.9). А это значит, что если значение концентрации сА окажется между обоими стационарными значениями, производная по времени будет отрицательной, концентрация реагента станет уменьшаться, приближаясь к значению

.

Таким образом, первое из этих значений относится к устойчивому режиму, второе – к неустойчивому.

Во-первых, кривая на рис. 6.9 справа не заходит дальше значения сА = сА0, поскольку правее от этой точки условие (6.15) означало бы отрицательную концентрацию вещества В, что невозможно.

Рис. 6.10. Траектории переходных процессов в фазовых координатах для автокаталитической реакции

Устойчивость экосистем.

Очень часто по тому же механизму потери устойчивости происходит разрушение биоценозов. Биоценоз – это система, состоящая из всех живых организмов (животных, растений, бактерий и др.), населяющих какой-либо участок Земли. При выбросе в окружающую среду вредных веществ в биоценозе развиваются компенсаторные механизмы, нейтрализующие вредные влияния. Поэтому до определенного предела среда ведет себя «почти нормально» – нормальное состояние устойчиво. Но при повышении загрязнения до некоторого критического уровня устойчивость теряется и биоценоз сразу, скачком, гибнет. Непонимание этого порождает неоправданное благодушие: дескать, выбрасываем отбросы – природа справляется; выбросим еще немного – тоже справится, в худшем случае станет немного грязнее. На деле требуются чрезвычайная осторожность и тщательное изучение устойчивости окружающей среды, а также огромная работа по повышению этой устойчивости.