3. Процессы в потоке. Идеальные потоки.

Поток как гомогенная движущаяся жидкая среда в аппарате непрерывного действия. Гетерогенность, влияние потока в иерархии: вниз на перенос, вверх на рабочую зону. Сложная структура потока: поле скоростей, перемешивание вдоль и поперек, время пребывания (объемная скорость) среднее и фактическое, проблема усреднения показателей.

Сложность структуры потока. Любой поток сложен по своей структуре. Сложность проявляется на различных уровнях, в разных масштабах, проявления ее весьма многообразны. Рассмотрим некоторые из них.

Нестационарность скорости. По этому признаку, как известно, потоки делятся на ламинарные и турбулентные. Ламинарный поток преимущественно стационарен. Разумеется, при изменениях, происходящих в системе (прежде всего при изменениях расхода жидкости), стационарность нарушается. Но установившийся ламинарный поток стационарен: в данной точке аппарата скорость проходящего через нее потока остается одной и той же. Турбулентный поток нестационарен по существу. Даже если никакие параметры в среднем не меняются во времени, поток все время испытывает хаотические колебания скорости, так называемые флуктуации, или пульсации.

Неоднородность поля скоростей. В разных частях потока скорости частиц жидкости различны как по величине, так и по направлению. Эти различия могут быть стационарными (например, параболический профиль скоростей в ламинарном потоке) и нестационарными: в турбулентном потоке максимум скорости наблюдается то в данной точке, то в соседней.

Крайние случаи неоднородности скоростей – это, с одной стороны, байпасы, а с другой – застойные зоны. В нашем случае под байпасом понимается часть потока, очень быстро проходящая от входа к выходу, почти не участвуя в процессе. Порции жидкости, попавшие в застойную зону, напротив остаются практически неподвижными и также выпадают из процесса. Неоднородность скоростей по направлению может проявляться по-разному. В турбулентном потоке флуктуации скорости направлены не только вдоль, но и поперек потока.

Кроме того, и в ламинарных, и в турбулентных потоках могут образовываться зоны циркуляции жидкости.

Описанные особенности структуры потока приводят к двум взаимосвязанным явлениям, оказывающим сильное влияние на ход химико-технологических процессов: возникновению перемешивания текущей жидкости и неравномерности времени пребывания.

Традиция, существующая в химии, склонна всегда считать перемешивание жидкости фактором, способствующим протеканию реакции. Но при рассмотрении этого фактора следует различать два случая: перемешивание в поперечном и в продольном относительно потока направлениях. Поперечное перемешивание интенсифицирует массообмен между осевой частью (ядром) потока и его периферией и тем самым, как правило, улучшает условия протекания реакции. Продольное перемешивание – это смешение частиц, которые недавно вошли в аппарат, с частицами, давно в нем находящимися, в которых процесс уже зашел далеко; чаще всего оно снижает движущую силу процесса и ухудшает его показатели. Поперечное перемешивание возникает либо под действием перемешивающих устройств (мешалок, устройств для барботажа и др.), либо под влиянием турбулентных пульсаций скорости, а также при наличии зон циркуляции.

Те же факторы вызывают и продольное перемешивание, но в этом случае, как правило, появляется еще сильно влияющий фактор – неравномерность распределения скоростей: те частицы, которые вследствие большей скорости ушли вперед, смешиваются с идущими впереди, отставшие – с нагоняющими их сзади. Очень часто именно эта неравномерность вносит основной вклад в продольное перемешивание. В ламинарном потоке оно может оказаться существенно бóльшим, чем в турбулентном. Так, при течении капельной жидкости в трубе переход от ламинарного режима (Re = 2000) к турбулентному (Re = 100 000) приводит к уменьшению интенсивности продольного перемешивания на несколько порядков.

Неравномерность времени пребывания – явление, в значительной мере эквивалентное продольному перемешиванию. Для частиц, уходящих вперед, время пребывания меньше среднего. Отстающие частицы характеризуются бóльшим временем пребывания. Среднее

время пребывания t текущей жидкости в аппарате, получаемое усреднением времен пребывания разных частиц, определяется простым соотношением:

Ее интерпретируют как объем движущейся фазы, проходящий через единицу объема аппарата за единицу времени.

Может показаться, что учитывать неравномерность времени пребывания частиц вещества необязательно: при малом времени пребывания частиц в рабочей зоне реакция пройдет недостаточно глубоко, зато если частицы долго находятся в этой зоне, то глубина протекания реакции велика. На выходе частицы взаимно перемешиваются, и степень превращения усредняется. Возникает вопрос: можно ли рассчитывать концентрации подстановкой в решение дифференциального уравнения кинетики значения t , пренебрегая неравномерностью t ?

Оказывается, что при одном и том же среднем времени пребывания частиц различные степени неравномерности дадут разные результаты.

Протекание химической реакции при неравномерном времени пребывания частиц вещества.

Частицы с малым временем пребывания выносят из аппарата много не прореагировавшего вещества, что снижает степень превращения. Правда, в частицах, долго находившихся в аппарате, реакция проходит очень глубоко. Но скорость большинства реакций снижается во времени. В этих частицах скорость реакции уже столь мала, что увеличение времени пребывания слабо сказывается на превращении. Проигрыш из-за быстро «проскочивших» через аппарат частиц не компенсируется выигрышем за счет частиц, задерживающихся в нем.

Можно предложить разные подходы к изучению структуры потока и влияния этой структуры на ход химических процессов. Наиболее полную информацию о структуре потока можно получить, зная скорость жидкости в любой точке аппарата, т. е. анализируя поле скоростей. В принципе это дает исчерпывающую картину потока. Точное описание поля скоростей может явиться материалом для решения любой задачи, относящейся к течению жидкости.

Но при таком подходе возникают труднопреодолимые препятствия. Прежде всего чрезвычайно трудна экспериментальная задача измерения скоростей во всех частях потока. В любом аппарате имеются области, где поток либо проходит сквозь сужения, либо резко заворачивает. Здесь почти невозможно измерить скорость, не нарушив структуру потока.

Но едва ли не важнее то, что знание поля скоростей позволяет решать практические задачи лишь в принципе. Как правило, это решение оказывается настолько сложным, что львиной долей информации воспользоваться не удается. Поле скоростей – сложная трехмерная структура, описание которой должно содержать функции по меньшей мере трех переменных (координат). Нестационарность (например, в турбулентном потоке) добавляет четвертую переменную – время. Математическое описание процесса обычно получается в виде систем нелинейных дифференциальных уравнений в частных производных. Решить такую систему даже с помощью мощных компьютеров удается лишь в простейших случаях.

Идеальные потоки без параметров или с минимумом таковых: вытеснения и смешения. Адекватность практическим представлениям, свойства, технологичность.

Еще один подход – построение упрощенных мысленных моделей потока. Упрощая сложную картину, такая модель должна в то же время отражать существенные для нас особенности потока, в первую очередь адекватно описывать особенности протекания в данном потоке химических, тепловых и массообменных процессов. Как и в других областях науки, в этом случае можно построить модели разной степени упрощения (см. разд. 1.3). На первом этапе создаются максимально упрощенные модели, которые называют идеальными потоками. Разработаны две модели идеальных потоков: идеальное вытеснение и идеальное смешение. Здесь отметим одну особенность этих моделей: они не содержат никаких параметров, отражающих специфику структуры потока. Единственный параметр – среднее время пребывания, определяемое пo формуле (4.1). В этом смысле все потоки идеального вытеснения подобны один другому; то же самое относится к потокам идеального смешения.

Существует довольно много задач, в которых описание реального потока моделью того или другого идеального потока оказывается достаточно точным. Если же точность такого приближения недостаточна, то переходят к более сложным моделям неидеальных потоков.

Эти модели уже содержат параметры, описывающие характер потока, начиная от однопараметрических моделей и кончая сложными комбинированными моделями, где число параметров может быть велико. Описанию некоторых таких моделей посвящен разд. 4.4.

Рассматривая какую-либо модель, я буду стараться осветить три вопроса:

1. Реалистичность и адекватность модели, т.е. насколько наша модель соответствует реальным объектам?

2. Свойства модели. Какая математическая модель соответствует данной схеме потока, каковы особенности решения уравнений математического описания и какие свойства объекта определяются этими решениями?

3. Технологическая оценка. Хорошо или плохо влияют на технологические показатели те или иные особенности объекта, описываемого моделью?

Этот подход относится как к моделям потоков, так и ко всему дальнейшему изложению.

ИВ (идеальное вытеснение): одномерный поток с одинаковой скоростью (концентрацией, температурой), временем пребывания.

Малый объем поперечного сечения потока является замкнутым. r=dC/dt. Переменный объем (переменное сечение) добавляет одно слагаемое.

В аппарате идеального вытеснения поток движется совершенно равномерно. В любом поперечном сечении все частицы имеют одинаковую скорость (рис. 4.1). Фронт потока движется, как твердый поршень, поэтому такой поток иногда называют поршневым (от англ. piston-flow).

Рис. 4.1. Схема потока идеального вытеснения

Рис. 4.2. Схема движения малого объема в потоке вытеснения

При анализе сложных процессов (например, реакций, проходящих с выделением и отводом тепла) определение идеального вытеснения приходится несколько конкретизировать – добавляется еще одно свойство. Не только скорость, но и концентрации, и температура в таком потоке выровнены по поперечному сечению. Для изотермических процессов эта выровненность получается автоматически, если выровнены скорости.

Для описания, анализа и расчета процессов существенны два следствия из определения идеального вытеснения.

1. Время пребывания всех частиц в потоке идеального вытеснения одинаково. Это практически единственный мыслимый поток, для которого формула (4.1) определяет не только среднее, но и конкретное время пребывания любой движущейся через аппарат частицы жидкости.

2. Выделенный в потоке малый объем, занимающий все поперечное сечение и движущийся вместе с потоком (рис. 4.2), в случае идеального вытеснения можно рассматривать, как замкнутый.

Действительно, в процессе течения ни одна частица не выйдет из этого объема ни вперед, ни назад (для этого она должна была бы двигаться с иной скоростью, чем остальные). Точно так же ни одна частица не войдет в рассматриваемый объем из таких же объемов, примыкающих к нему спереди и сзади. Поэтому кинетика реакции при постоянном объеме будет описываться уравнениями

Если объем непостоянен, то выражения усложняются, но в принципе в любом случае можно записать соответствующую систему

дифференциальных уравнений.

Субстанциональная производная – начало координат движется с объемом. Обычная производная равна нулю. Поверка/проект. Реакция 1 порядка как простой пример.

В уравнении (4.3) есть одна тонкость. Время, входящее в него, отсчитывается в объеме, движущемся вместе с потоком. Поэтому в его левой части – не совсем обычная производная: дифференцирование производится для движущейся вместе с субстанцией системы координат. Это субстанциональная производная. Если измерять концентрацию любого вещества, находясь неподвижно в любой точке аппарата, то получим обычную производную. Ясно, например, что в стационарном режиме концентрация любого вещества в этой точке не меняется во времени: подходя к ней, жидкость всякий раз приобретает одно и то же значение концентрации, поэтому обычная производная равна нулю. Но субстанциональная производная и в стационарном режиме – не нулевая, поскольку при прохождении данной точки реакция в движущейся жидкости продолжает идти.

Необходимо учитывать, что интегрирование субстанциональных производных ничем не отличается от интегрирования обычных. Решение системы (3.47) следует искать в пределах от t = 0 (жидкость вошла в аппарат) до (выход жидкости из аппарата). В этом случае получатся концентрации веществ на выходе из аппарата. Это поверочный расчет. Для проектного расчета в решение системы подставляют требуемые значения концентраций и находят , а затем по формуле (4.1) определяют объем аппарата.

Реакция 1 порядка как простой пример.

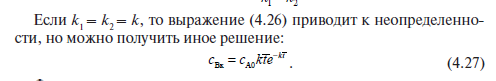
ИС (идеальное смешение): кинетика в точечном объеме выполняется во всем объеме. Входной скачок. Среднее время пребывания. Открытость:rdC/dt. Субстанция j, контур – аппарат, время dt. Вход В_j=c_j0vdt. Уход У_j= c_jvdt. И_j-С_j=V_ar_jdt. Накопление Н_j=V_adc_j. В итоге c_j0v-c_jv+V_ar_j=V_adc_j/dc_j.

Теперь опишем аппарат идеального смешения. Представим себе аппарат с мешалкой, через который проходит поток жидкости (рис. 4.3). Мощность мешалки такова, что поступающая жидкость мгновенно перемешивается с массой, уже находящейся в аппарате. Таким образом, все, что попадает в аппарат идеального смешения, мгновенно равномерно распределяется по всему его объему.

Рис. 4.3. Концентрации веществ на входе, в объеме и на выходе аппарата смешения; v – расход потока

Перечислю важнейшие следствия из этого определения.

1. Концентрации всех веществ и температура равномерно распределены по объему аппарата. В любой паре точек в аппарате любая из этих величин имеет в данный момент одно и то же значение.

2. Для уточнения следствия 1 следует рассмотреть две точки, о которых заранее трудно сказать, находятся ли они в аппарате: точки входа и выхода потока. На выход поток выносит ту жидкость, которая находится в аппарате. Поэтому на выходе из аппарата идеального смешения концентрации и температура те же, что и в объеме. На входе в аппарат концентрации и температура претерпевают скачок: исходные значения параметров потока, мгновенно смешивающегося с содержимым аппарата, соответственно мгновенно изменяются до тех значений, которые характеризуют режим внутри аппарата и

на выходе из него.

3. Время пребывания в аппарате идеального смешения распределено неравномерно. Действительно, распределяя по объему вошедшую порцию жидкости, наша идеальная мешалка пошлет некоторые частицы из этой порции к выходу и они сразу уйдут из аппарата, в то время как другие, попавшие в иные части аппарата, могут задерживаться в нем весьма надолго.

4. Аппарат, как и любая его часть, принципиально открыт.

Смешение в каждый момент и в каждой точке подводит одни порции жидкости и отводит другие. Замкнутых объемов нет. Отсюда следует, что зависимости (3.47) к потоку смешения неприменимы. Для его описания следует искать иной подход.

Здесь можно использовать то обстоятельство, что во всех точках аппарата концентрации и температура, а стало быть, и скорость реакции одинаковы. Аппарат идеального смешения – типичный пример объекта с сосредоточенными параметрами (см. разд. 1.3). Это позволяет очень просто записать уравнения баланса (1.11) или (1.12).

Дело в том, что во всех точках такого объекта интенсивность источника (или стока) – одна и та же. В результате весь объем аппарата можно рассматривать как элементарный объем.

Воспользуемся рис. 3.3 и составим схему материального баланса по веществу J. Символ J будет означать «какое-либо из веществ», и все, что получено для него, верно в общем виде для любого из участников реакции. Таким образом, уже выбраны субстанция (вещество J) и контур, охватывающий весь аппарат. Выберем в качестве интервала времени дифференциал dt и обсудим статьи баланса.

Вход. За время dt в аппарат входит объем жидкости vdt. Умножив этот объем на концентрацию входящей жидкости, получим

Уход. Определяем так же, как вход, при этом учитываем, что концентрация cJ имеет одно и то же значение как на выходе из аппарата, так и в любой точке внутри него. Таким образом,

Источник и сток. Вспомним, что мы определили скорость реакции как количество вещества, превращающегося в единицу времени в единице объема. При этом формула (3.55) определяет скорость по веществу, так что в нее входят и стадии, в которых вещество образуется (источник J), и те, где оно расходуется (сток). Поэтому, умножив

скорость по J на объем аппарата и на интервал времени, получим разность источника и стока:

Накопление. Если за время dt концентрация изменится на величину dcJ , то изменение количества вещества в объеме (накопление) составит

Нестационарное и стационарное поведение, со средним временем. Размерность системы уравнений. Открытость/закрытость. Варианты записи. Стационарный режим при измерении скорости реакции.

Каждая из формул (4.32) и (4.33) задает систему уравнений, поскольку ее следует записать для каждого из веществ, участвующих в реакции. Но в случае стационарного процесса часть уравнений (4.33) целесообразно заменить уравнениями стехиометрических ин-

вариантов.

Обратим внимание на одну особенность выражения (4.32). В его правой части – производная от концентрации по времени, умноженная на объем, а в левой на объем умножена скорость реакции, но имеются еще два члена. Отсюда следует, что практически никогда в таком потоке скорость реакции не равна производной dc/dt. Это объясняется открытостью данной системы. Лишь если мы исключим поток (приравняем v к нулю), т.е. замкнем объем, эти две величины сравняются и мы перейдем к описанию периодического процесса – выражению (4.3).

Если поделить выражения (4.32) и (4.33) на v и учесть соотношение (4.1), то получим формулы, часто более удобные для расчетов:

В стационарном режиме в потоке смешения скорость реакции может быть получена как отношение конечного изменения концентрации к среднему значению времени, за которое изменение произошло. Следует лишь учесть, что в нестационарном режиме это соотношение неверно.

Рассмотрим сравнительно простой случай – стационарное протекание реакции в потоке идеального вытеснения. Это будет иной подход по сравнению с тем, что применен выше.

Так как мы считаем в идеальном вытеснении параметры выровненными в поперечных направлениях, то изменения происходят только вдоль продольной оси х. Поэтому элементарный объем может занимать все поперечное сечение аппарата, но будет иметь бесконечно малую длину dx (рис. 4.4).

Обратите внимание на различие между схемами на рис. 4.2 и 4.4. На рис. 4.2 изображен малый движущийся объем жидкости, на рис. 4.4 – малая неподвижная часть аппарата, через которую проходит поток.

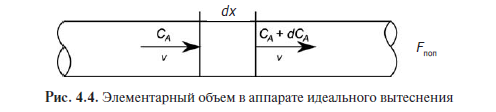
Рис. 4.4. Элементарный объем в аппарате идеального вытеснения

Преимущество ИВ. Качественные сопоставления: концентрационная (порядок), температурная (энергия активации) зависимость

Сопоставление идеальных потоков. О реалистичности моделей идеальных потоков. Идеальные потоки – сильно упрощенные модели.

Примеры: Так, к идеальному вытеснению близок поток жидкости или газа, проходящий через достаточно длинный аппарат, заполненный слоем зернистого материала (насадочная колонна, реактор с неподвижным слоем катализатора, шахтная печь). Зернистый слой интенсивно выравнивает поток. В меньшей степени можно применить эту модель к потоку в пустой трубе, особенно в ламинарном режиме (см. разд. 4.1).

Близко к идеальному смешению течение жидкости через аппарат с достаточно мощной мешалкой или через барботажный слой. В том же барботажном слое течение газа плохо описывается данной моделью, но зачастую нам нужно описать именно движение жидкости, считая, что газ не сильно отклоняется от идеального вытеснения.

Сопоставление идеальных потоков.

Каждый из идеальных потоков отличает предельная равномерность. В идеальном вытеснении это равномерность скоростей и времени пребывания, в идеальном смешении – равномерность концентраций и температуры по объему.

Стационарный процесс в потоке идеального вытеснения описывается системой дифференциальных уравнений (4.3).

Для идеального смешения этот случай описывается уравнениями (4.33) или (4.35) –

конечными уравнениями, не содержащими операторов дифференцирования.

Лишь в нестационарном режиме в описании появляются производные. Объясняется это тем, что в идеальном смешении нулю равны производные по координатам – градиенты концентраций и температуры. В связи с этим процесс в потоке смешения можно описывать так, будто он целиком происходит в одной точке (от точки к точке ничто не меняется). И в нестационарном процессе аппарат идеального смешения ведет себя «как точка» – все изменения происходят во всем объеме одновременно.

Аппарат идеального вытеснения – объект с распределенными параметрами: в нем параметры процесса меняются от точки к точке.

Правда, это простейший из таких объектов – одномерный, поскольку рассматриваются изменения лишь в продольном направлении, а поперек потока все считается выровненным. Тем не менее описание идеального смешения еще проще, что привлекательно с точки зрения математической обработки модели. Поэтому, как увидим далее, ряд более сложных моделей строится на основе модели смешения.

Теперь посмотрим на примере простейшей реакции 1-го порядка А → В, как равномерность или неравномерность распределения параметров влияет на ход химической реакции. Многие сделанные при этом выводы будут верны для большинства формально простых реакций, обратимых реакций, а также для процессов массо- и тепло-

обмена, описание которых аналогично описанию обратимой реакции 1-го порядка.

В начале проведем качественный анализ. Равномерность времени пребывания в идеальном вытеснении способствует глубокому протеканию реакции (см. пример 4.1), так что с этой точки зрения преимущество следует отдать потоку вытеснения. Для того чтобы определить, как влияет на процесс равномерность концентраций в потоке смешения, построим график изменения концентрации реагента А по длине аппарата идеального вытеснения либо идеального смешения (рис. 4.5). На графике х = 0 – вход в аппарат; х = L – выход. Значения х < 0 и х > L соответствуют трубам, подводящим жидкость к аппарату и отводящим прореагировавшую смесь. Будем считать заданными исходную cA0 и конечную cAк концентрации реагента.

Рис. 4.5. Изменение концентрации реагента по длине аппарата для идеальных потоков

В идеальном вытеснении легко связать пройденный частицей путь с временем протекания реакции в этой частице:

Уравнение (4.14) соответственно получит вид

В аппарате смешения картина совершенно иная. На входе происходит скачок концентрации реагента А до значения, которое дальше сохраняется вплоть до выхода. По всей длине аппарата

Если теперь рассмотреть любое поперечное сечение обоих аппаратов, то очевидно, что значение сА в аппарате вытеснения окажется больше соответствующего значения в аппарате смешения. Скорость реакции, пропорциональная сА, во всех сечениях аппарата, кроме последнего (на выходе), также будет большей в аппарате вытеснения, чем в аппарате смешения. Получить картину, показанную на рис. 4.5 (одинаковые начальные и одинаковые конечные сА), можно только в том случае, если объем аппарата смешения больше объема аппарата вытеснения. Отсюда можно сделать два вывода:

1) аппарат вытеснения обеспечивает большую эффективность процесса;

2) на кинетику реакции влияет не только химизм, но и характер потока.

Таким образом, анализ распределения и времени пребывания, и концентраций приводит к выводу о большей эффективности потока вытеснения. Правда, судить об эффективности только по скорости протекания реакции опасно. Конструкции аппаратов, близких к обоим идеальным типам, различны. В частности, интенсивное перемешивание способствует массо- и теплообмену. Часто процессы, для которых важен перенос тепла и вещества, проще оформить в аппарате с перемешиванием, и тогда возникает проблема: чем жертвовать – простотой конструктивного оформления или малым продольным перемешиванием.

Сопоставление произвольной реакции в потоках ИВ и ИС вычислительными методами: равная конверсия (высокая и низкая), равный объем, равная скорость. Наилучший и наихудший поток.

Для 0, 1 и 2 порядка еще возможно аналитическое решение.

Решение вопроса об эффективности того или иного потока должно, разумеется, базироваться на количественных оценках, к которым мы и перейдем. По-прежнему будем анализировать реакцию 1-го порядка А → В.

Можно сопоставить выражения (4.14) и (4.39). Задав ряд значений , .рассчитаем при каждом из них степень превращения в потоках идеального вытеснения χвыт и идеального смешения χсм. Данные расчета сведены в следующую таблицу.

Результаты последнего сопоставления очень показательны. Если требуется невысокая степень превращения (менее 0,9), то проигрыш вследствие перехода от идеального вытеснения к идеальному смешению не слишком велик. Оценивая эффективность, нужно учитывать и иные факторы. Но если требуется степень превращения 99% или выше, различие в необходимых объемах столь велико (в десятки или даже сотни раз), что ясно: следует применять аппараты, максимально близкие к идеальному вытеснению.

Вывод о том, что в аппарате вытеснения глубина превращения выше, чем в аппарате смешения, и что преимущество этого потока возрастает по мере роста требуемой степени превращения, верен для изотермических необратимых и обратимых реакций любого положительного порядка, а также для большинства тепло- и массообменных процессов. Можно показать, что по глубине протекания процесса поток идеального вытеснения теоретически наилучший всегда, когда скорость процесса снижается по мере его протекания.

Ускорение: автокатализ, разветвление цепи, биохимические, автотермические, матричные реакции.

Нужно также иметь в виду, что существует ряд процессов, в которых закон изменения скорости реакции по ходу процесса иной. Вначале скорость реакции мала, постепенно она нарастает и затем, достигнув максимума, начинает снижаться (рис 4.6). Объясняется

это тем, что во время процесса вырабатывается какая-либо субстанция (вещество или энергия), ускоряющая его протекание. Вначале этой субстанции мало, поэтому процесс идет медленно. С течением времени он самоускоряется до максимума, после чего скорость начинает уменьшаться вследствие нехватки исходного вещества. Отмечу четыре группы таких процессов.

Рис. 11.6. Изменение по времени скорости реакции с самоускорением

1. Автокаталитические реакции, в которых один из продуктов реакции ускоряет процесс. Пока этого продукта мало, реакция медленная. Накопление катализатора ведет к ускорению реакции до тех пор, пока в конце процесса убыль исходных веществ не обусловит снижение скорости.

2. Биохимические реакции, вызываемые микроорганизмами – брожение, ферментация. На начальной стадии процесса его скорость возрастает в связи с интенсивным размножением микроорганизмов. В конце процесс замедляется вследствие недостатка «пищи».

3. Автотермические процессы, в которых вначале за счет тепла экзотермической реакции происходит разогрев, ведущий к росту скорости.

4. Процессы кристаллизации. В начальной стадии процесса скорость растет благодаря увеличению числа зародышей кристаллизации. Затем образование новых зародышей прекращается и скорость снижается из-за уменьшения пересыщения.

Если процесс такого типа проводить в аппарате вытеснения, то на начальном отрезке аппарата скорость реакции мала и эта его часть используется неэффективно. В таком случае более эффективным может оказаться аппарат смешения: в нем несложно поддерживать высокую концентрацию катализатора, микроорганизмов, зародышей кристаллизации или высокую температуру. Причем эта оптимальная концентрация или температура поддерживается во всем объеме аппарата. После того как процесс пройдет через максимум скорости, он будет идти как процесс с падающей скоростью. Поэтому на этом этапе (на «хвосте» процесса) смесь выгодно вывести из аппарата смешения

и направить в аппарат вытеснения.

В ряде подобных случаев процесс можно проводить и в аппарате вытеснения, но тогда для ускорения начальной стадии процесса осуществляют циркуляцию: часть потока, выходящего из аппарата, возвращают на его вход (рис. 4.7). С этим циркуляционным потоком в начальный участок аппарата вносится «затравка», ускоряющая процесс. Можно отметить, что циркуляцию вообще можно рассматривать как один из механизмов продольного перемешивания. Естественно, если агент, ускоряющий процесс, – это тепло, то не нужно смешивать входящий и циркулирующий потоки, тепло от уходящей жидкости ко входящей может быть передано через стенку.

Сложные реакции в идеальных потоках: селективность. Потеря селективности для последовательных реакций в ИС. Параллельные реакции одинакового порядка – независимость селективности от потока. Дифференциальная селективность. Разные порядки. Средняя селективность – это интегральная селективность.

Сложные реакции в идеальных аппаратах. При проведении сложных реакций с побочными стадиями обычно главной задачей является достижение высокой селективности. Зачастую ради этого жертвуют степенью превращения: недопревратившиеся реагенты можно отделить от вышедшей из аппарата смеси и вернуть в начало процесса.

В результате стоимость переработки возрастает на величину стоимости процесса разделения. Низкая же селективность означает, что, во-первых, часть исходных веществ затрачивается бесполезно (переходит в ненужные побочные продукты); во-вторых, эти побочные продукты также приходится отделять (затраты на разделение могут быть даже большими, чем при низкой степени превращения); в-третьих, с побочными продуктами после их отделения нужно что-то делать. Просто выбросить их, как правило, нельзя: загрязнение окружающей среды в наше время становится одной из тяжелейших проблем, стоящих перед человечеством. Обезвреживание или уничтожение побочных продуктов ложится тяжелым грузом на экономику процесса. Характер влияния структуры потока на протекание сложных реакций отличается большим разнообразием. \

Рассмотрим два простых случая: реакцию с последовательной побочной стадией и реакцию с параллельной побочной стадией. Для последовательной побочной стадии вначале проведем качественный анализ. Реакция А → В → С, где В – целевой продукт, а С – побочный. На качественном этапе кинетические порядки стадий несущественны.

Построим график, аналогичный приведенному на рис. 4.5 (изменение концентрации по длине аппарата), но по оси ординат отложим изменение концентрации целевого продукта В (рис. 4.8). По оси абсцисс по-прежнему – координата длины от входа к выходу.

Рис. 4.8. Изменение концентрации целевого продукта по длине аппарата: 1 – идеальное вытеснение, 2 – идеальное смешение

Учтем, что скорость второй (побочной) реакции тем выше, чем больше концентрация В. Изменение показателей процесса по длине в аппарате вытеснения такое же, как изменение по времени в периодическом процессе, проанализированное в конце разд. 3.2 (см. табл. 3.2). Вначале концентрация В мала, а концентрация А велика; скорость образования В – большая, а скорость побочной реакции – маленькая. Селективность при этом близка к 1. Затем, по мере исчерпания А и накопления В, скорость первой стадии снижается, скорость второй растет и селективность уменьшается. В аппарате же смешения по всей длине мала концентрация реагента А и велика концентрация В. Во всем объеме аппарата процесс протекает с минимальной селективностью. Если обе стадии 1-го порядка, то,

Для параллельной реакции (В – целевой продукт)

А → В

А → С

влияние структуры потока на селективность зависит от соотношения порядков основной и побочной стадий. Аналитические выражения для σ не всегда достаточно просты, поэтому легче провести анализ на основе другой характеристики – отношения скоростей образования обоих продуктов:

Величина ω не равна σ, но симбатна ей: чем больше отношение скоростей, тем больше селективность. Если обе стадии одинакового порядка, то ω зависит только от соотношения констант скоростей обеих стадий:

В этом случае селективноcть не меняется по ходу реакции (если температура постоянна) и не зависит от характера потока. Если же порядки разные (n1 и n2), то

Теперь селективность зависит от концентрации А. Например, если целевая (первая) реакция 1-го порядка, а побочная – 2-го, то ω обратно пропорциональна сА.

Обратимся к рис. 4.5. При заданной степени превращения А его концентрация в любом поперечном сечении аппарата смешения будет ниже, чем в соответствующем сечении аппарата вытеснения. Значит, в случае, когда n1< n2, процесс в аппарате идеального смешения будет проходить хотя и медленнее, но зато с существенно большей селективностью, т. е. именно аппарат смешения окажется наилучшим.

Нетрудно понять, что если целевая реакция 2-го порядка, а побочная – 1-го, то все преимущества будут у аппарата вытеснения.

Время пребывания в потоке. Простой метод исследования и диагностики, но полезный только при 1 кинетическом порядке.

Имеются условия (в первую очередь связанные с необходимостью получения высокой степени превращения), когда продольное перемешивание сильно ухудшает показатели процесса.

В этих случаях имеет место не только резкое различие в эффективностях аппаратов идеального вытеснения и идеального смешения, но и заметное влияние небольших отклонений от идеального вытеснения. Даже в аппаратах со слабыми отклонениями от равномерности времени пребывания процесс идет не так, как при идеальной модели.

Наблюдаются и такие случаи, когда аппарат (или участок аппарата), в котором создается интенсивное перемешивание, не описывается с достаточной точностью моделью идеального смешения.

При всей привлекательности самого исчерпывающего подхода – изучения поля скоростей, он слишком сложен. В ряде случаев его использование дает важные результаты, но часто желательно воспользоваться более простым методом. Для этого может служить исследование распределения времени пребывания жидкости в аппарате. Правда, при таком подходе многое теряется; например, мы не узнаем, каковы скорости в разных частях

аппарата. Действительно, рассмотрим рис. 4.10. На нем схематически изображены эпюры скорости в поперечных сечениях трех аппаратов. В одном аппарате профиль скоростей – парабола с максимумом на оси потока, в другом – поток идет в основном вдоль левой стенки, в последнем – поток в среднем равномерен по сечению, но из-за турбулентных пульсаций одни его частицы обгоняют другие. Однако с той точки зрения, которую мы сейчас излагаем, эти аппараты неотличимы один от другого. Каждый из них часть жидкости проходит быстрее, чем поток в среднем, часть – медленнее. Если для двух аппаратов эти части одинаковы, то и потоки представляются одинаковыми. Таким образом, мы обедняем картину потока, исключая много важных подробностей.

Рис. 4.10. Эпюры скоростей при неравномерности трех видов: а – симметричной; б – несимметричной; в – хаотичной

При этом мы получаем серьезные преимущества. Во-первых, эксперимент при таком подходе прост. Во-вторых, данные опытов легко поддаются количественной обработке и трактовке: из всех переменных остается одна – время пребывания. В-третьих, полученные результаты достаточны для многих случаев. В-четвертых, если

этих данных окажется недостаточно для анализа процесса, то в дальнейшем можно перейти к снятию поля скоростей. При этом информация о распределении времени пребывания поможет наилучшим образом спланировать соответствующий эксперимент и упростить обработку его результатов.

Наша цель – узнать, какое количество текущей жидкости будет находиться в аппарате в то или иное время. Отдельные частицы неразличимы, поэтому, чтобы различить их, выделим из всей совокупности те из них, которые вошли в аппарат в некоторый зафиксированный момент и примем его за начало опыта. Таким образом, выделенные частицы образуют представительную выборку из генеральной совокупности частиц, движущихся через аппарат. Для выделения интересующих нас частиц пометим жидкость, входящую в аппарат в момент, который примем за начало опыта (t= 0). С этой целью во входящий поток быстро добавляем порцию какой-либо примеси, называемой индикатором, или трассером. Индикатор должен быть легко количественно определим. Кроме того, его добавление не должно влиять на характер потока (в частности, его следует вводить мало, чтобы существенно не изменять расход), а сам он должен двигаться вместе с потоком, ни с чем не реагируя и не сорбируясь. Начиная с момента t = 0 на выходе из аппарата измеряют концентрацию индикатора с_и как функцию t. Типичный график зависимости с_и (t) показан на рис. 4.11.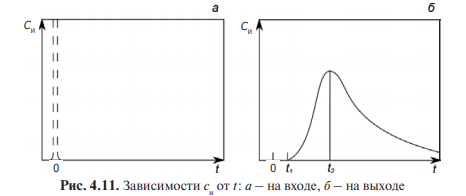

В момент t = 0 на входе резким импульсом вводится индикатор (рис. 4.11,а). При мгновенной подаче конечного количества индикатора его концентрация будет бесконечной. Реально получается более или менее узкий и высокий импульс. На выходе (рис. 4.11, б) вначале с_и= 0: ни одна частица индикатора не успела дойти до выхода. В момент t 1 выхода достигает самая быстрая часть потока, появляется индикатор. Далее его концентрация нарастает до момента t 2 , а затем начинает убывать: основная масса потока прошла, выходят те части индикатора, которые попали в зоны циркуляции или застоя. Выход этих порций обычно продолжается долго; лишь через большой промежуток времени практически весь индикатор покидает аппарат.

Обозначим количество индикатора, находящееся в данный момент в аппарате, через g_и. В начальный момент в аппарате находилось все введенное в поток количество индикатора g_и0. Концентрацию индикатора на выходе обозначим через с_и. Рассмотрим произвольный текущий момент. За единицу времени из аппарата выйдет объем жидкости, равный расходу v; за бесконечно малый промежуток dt, отсчитываемый от данного момента, – объем vdt. Количество индикатора, вышедшего из аппарата за промежуток dt, составит

Знак «–» означает, что количество индикатора убывает, т.е. индикатор уходит из аппарата.

Дальнейший анализ целесообразно вести, перейдя к безразмерным величинам. В эксперименте с_и тем больше, чем больше введенное количество индикатора g_и0. Но при изучении потока величина g_и0 – несущественная, она определяется случайными обстоятельствами опыта. Безразмерная концентрация не должна от нее зависеть.

Переходим к безразмерным единицам:

Для каждой величины u на исследуемом объекте выберем характерное значение u0 .

v=u/u0

Безразмерные величины С и τ имеют тот же физический смысл концентрации и времени, что и размерные. Изменились лишь масштабы, в которых они измеряются. Преобразуем уравнение (4.46), используя сначала формулы (4.51) и (4.52), а затем (4.47) и (4.48) и вынося постоянную величину t за знак дифференциала:

Доля от общего количества проходящей через аппарат жидкости, равная Сdτ, имеет время пребывания τ с точностью до dτ. Безразмерная концентрация индикатоpa С равна плотности вероятности (дифференциальной функции распределения) времени τ как случайной величины.

Для функции С(τ) (функция С) верны все свойства, выраженные формулами (2.3) – (2.5), с некоторыми уточнениями, связанными со следующей особенностью: С = 0 при τ < 0 (4.54) Смысл формулы (4.54) таков: вероятность того, что частица выйдет из аппарата раньше, чем войдет в него, равна нулю. Поэтому в интегралах (2.4) и (2.5) нижний предел можно заменить на 0.

При импульсной подаче индикатора на выходе имеем C(τ). Чтобы получить F(τ), характер подачи (сигнал на входе) должен быть иным: до момента τ = 0 концентрация индикатора равна нулю; в этот момент (теоретически мгновенно) концентрация скачком возрастает до 1 и далее остается на этом уровне (рис. 4.12,а).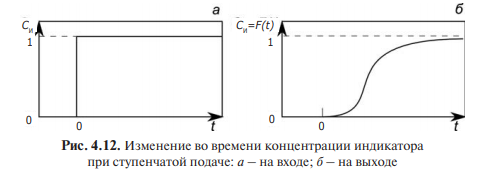

Некоторые другие величины, характеризующие пребывание в потоке

Среднее время пребывания.

Размерный вид формулы:

Рассчитав t по формуле, можно решить одну из двух задач: либо по известному Va рассчитать расход жидкости, либо по известному v – неизвестный объем.

Дисперсия времени пребывания

По размерным значениям расчет можно вести, пользуясь формулой

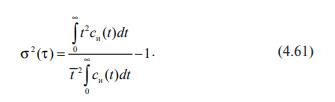
Распределение времени пребывания и степень превращения.

В случае изотермической необратимой реакции 1-го порядка степень превращения однозначно определяется константой скорости, средним временем пребывания и видом дифференциальной функции распределения. Такая же однозначность имеет место при протекании обратимой реакции и любой сложной реакции, все стадии которой проходят по первому порядку. Уравнения тепло- и массопередачи аналогичны уравнению обратимой химической реакции 1-го порядка, поэтому подчиняются аналогичным закономерностям:

где Kт – коэффициент теплопередачи; T1 и T2 – температуры теплоносителей.

Для реакций не 1-го порядка приходится учитывать ряд дополнительных факторов. Но во многих случаях первоначальную оценку влияния потока можно получить и для них, имея данные о распределении времени пребывания.

Законы распределения времени пребывания для идеальных потоков

Рассмотрим, какой вид имеют дифференциальная и интегральная функции распределения для аппарата идеального вытеснения. Так как время пребывания всех частиц одинаково, то при τ < 1 выхода не достигнет ни одна меченая частица: С = 0. При τ > 1 также С = 0: все меченые частицы уже прошли. Функция С(τ) отлична от нуля лишь при τ = 1. Но по условию (4.67)

Если функция отлична от нуля только в одной точке, а площадь под ее кривой конечна, то в этой точке функции придется приписать бесконечное значение

единица в скобках – это значение времени, при котором происходит бесконечный импульс. Изобразить график δ-функции невозможно; график С(τ) для некоего режима, близкого к идеальному вытеснению, показан на рис. 4.13. Это весьма узкий, крутой и высокий пик.

Интегральная функция для данного случая показана на рис. 4.14. Функция F(τ) = 0 при τ < 1. При τ= 1 происходит ее скачок, и при 1 < τ < +∞ функция F(τ) = 1: из аппарата уже вышла вся жидкость, вошедшая в него в момент τ= 0.

Для получения на выходе функции С(τ) необходимо подать индикатор на вход по закону δ-функции (см. рис. 4.11,а). Если на выходе желательно получить F(τ), сигнал на входе должен быть интегралом от δ-функции (см. рис. 4.12,а). В потоке идеального вытеснения входной сигнал, не искажаясь, переносится от входа к выходу за время τ= 1. Выходной сигнал, соответственно С(τ) или F(τ), совпадает по форме с входным, но сдвинут по оси абсцисс на единицу. Основное свойство δ-функции выглядит так. Для любой функции φ(τ) справедливо равенство

Функция С(τ) для потока идеального смешения.

Результат тот же, что и полученный на базе иных соображений (из рассмотрения материального баланса).

Рассмотрим протекание необратимой реакции 2-го порядка А → В в потоке, характеризуемом дифференциальной функцией распределения времени пребывания С(τ).

Сегрегация и перемешивание. Точность при других порядках. Примеры функций распределения по времени пребывания, их получения.

Уровни перемешивания. Сегрегация. Итак, двумя способами мы получили два разных выражения для реакции 2-го порядка, проходящей в потоке идеального смешения: (4.42) из материального баланса и (4.84) из распределения времени пребывания. Расчет χ по обеим формулам графически представлен на рис. 4.16.

Рис. 4.16. Степень превращения для реакции 2-го порядка в аппарате смешения: 1 – по формуле (4.84); 2 – по формуле (4.42)

При больших значениях χ различие между результатами двух расчетов весьма существенно. Горизонтали на графике показывают: в соответствии с уравнением (4.84) для достижения χ = 0,8 нужен аппарат вдвое меньшего объема, чем рассчитанный по уравнению (4.42); если же нужно обеспечить χ = 0,925, то эта разница достигнет 3,7 крат. Какое же уравнение правильно? В каком выводе допущена ошибка и какая?

«Сортируя» жидкость, вытекающую из аппарата, по времени пребывания, мы предполагали, что каждая частица проходит аппарат сама по себе. На деле же частицы взаимно смешиваются. Это смешение не влияет на ход реакции 1-го порядка: в ней каждая молекула реагирует независимо от того, какие молекулы ее окружают. Но в реакции 2-го порядка (и любого другого, кроме нулевого и 1-го) вероятность вступления молекулы в реакцию зависит от вероятности ее столкновения с другими молекулами. А эта вероятность зависит от концентрации и изменяется при смешении частиц.

Однако было бы слишком поспешно заключить из сказанного, что при расчете по формуле (4.84) результат всегда неверный, а при расчете по (4.42) всегда верный. Дело в том, что в реальных случаях отдельные частицы смешиваются одна с другой в разной степени.

По определению, в аппарате идеального смешения каждая входящая частица полностью перемешивается со всеми другими и составляющие ее молекулы равномерно рассеиваются по всему аппарату (рис. 4.17, а). При этом формула (4.42) будет верной. Но возможен и иной случай.

Представим себе другой (также идеализированный) характер движения. Входящие в аппарат частицы жидкости мгновенно равномерно распределяются по его объему : с этой точки зрения в аппарате наблюдается идеальное смешение. Но каждая частица движется в потоке как единое целое, не перемешиваясь с окружающими частицами. Поэтому хотя в среднем концентрация вещества во всех частях аппарата одинакова, однако если рассмотреть маленький его участок в увеличенном масштабе (рис. 4.17, б), то станет видно, что эта средняя концентрация складывается из значений, хаотически колеблющихся от частицы к частице. В первом случае говорят об идеальном смешении на микроуровне, во втором – об идеальном смешении на макроуровне при полной сегрегации (разделении) на микроуровне.

Итак, для расчета протекания реакции 1-го порядка достаточно знать дифференциальную функцию распределения времени пребывания. Для реакций более высоких (а также и более низких) порядков этого уже недостаточно, так как начинает сказываться ограниченность подхода, не учитывающего особенности перемешивания в аппарате. Понятие о сегрегации – один из путей преодоления этой ограниченности. К сожалению, строгих количественных характеристик для случаев, промежуточных между полным смешением на микроуровне (сегрегация равна нулю) и полной сегрегацией (равной единице), видимо, пока не имеется. Можно говорить лишь о большей или меньшей сегрегации.

В случае идеального вытеснения, если за частицу принимать малый движущийся объем, занимающий все поперечное сечение, сегрегация всегда полная: такие частицы в этом потоке между собой не перемешиваются. В потоках смешения в принципе возможны ситуации с любой степенью сегрегации. Если нет оговорки, то поток считают несегрегированным. При гомогенных, не слишком быстрых реакциях в турбулентных потоках степень сегрегации близка к нулю.

Повышение вязкости и переход в ламинарный режим увеличивают сегрегацию.

Рис. 4.17. Изменение концентрации по длине в увеличенном масштабе: а – идеальное смешение на микроуровне; б – полное смешение на макроуровне при полной сегрегации

Высокой может быть сегрегация в случае очень быстрых реакций: за время их протекания частицы не успевают перемешаться. В дисперсных фазах многофазных потоков сегрегация может быть близка к единице. Так, если реакция идет в твердых частицах, проходящих через аппарат (например, в псевдоожиженном слое), то сегрегацию можно считать полной. Сегрегация дисперсной фазы эмульсии или пены зависит от того, насколько часто сливаются (коалесцируют) капли или пузыри.

Ход реакции не 1-го порядка зависит не только от степени сегрегации, но и от иных особенностей потока. Так, если в аппарате чередуются зоны с разным характером потока, то степень превращения зависит от порядка чередования этих зон.

Пример 4.10. Рассмотрим протекание необратимой реакции А → В в двух системах последовательно соединенных и равных по объему аппаратов идеального смешения и идеального вытеснения. В первой системе вначале включен аппарат вытеснения, а во второй– аппарат смешения. Среднее время пребывания в каждом аппарате – 1 мин. Концентрация реагента на входе – 1 кмоль/м3. Расчет проведем для двух случаев: 1) реакция 1-го порядка, k = 1 мин-1; 2) реакция 2-го порядка; k = 1 м3/(кмоль·мин).

Для реакции 1-го порядка и первой системы концентрация вещества А после первого аппарата определяется по формуле